1.问题描述
旅行商问题(Travelling Salesman Problem, 简记TSP,亦称货郎担问题):设有n个城市和距离矩阵D=[dij],其中dij表示城市i到城市j的距离,i,j=1,2 … n,则问题是要找出遍访每个城市恰好一次的一条回路并使其路径长度为最短。
利用模拟退火算法(Simulate Anneal,SA)解决上述旅行商问题。
2.算法设计
1) 问题分析
在TSP问题中,n个城市的任何一种排列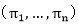 均是问题的一个可能解。其中
均是问题的一个可能解。其中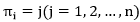 表示第i个到达的城市是j,并且默认
表示第i个到达的城市是j,并且默认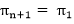 。当规定了出发城市时,解空间的规模是(n-1)!。因此难以利用深度搜索或广度搜索等穷举方法进行求解。
。当规定了出发城市时,解空间的规模是(n-1)!。因此难以利用深度搜索或广度搜索等穷举方法进行求解。
模拟退火算法来源于固体退火原理,是一种基于概率的算法。从某一较高初温出发,伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解,即在局部最优解能概率性地跳出并最终趋于全局最优。因此能够有效得解决TSP问题。
2) 参数设置
模拟退火算法的表现和参数设置有着很大关系。在经过实验分析之后,实验确定了一组较为合适的参数,该组参数权衡了运行时间和解空间的质量等因素。参数如下:
- 初始温度t0 = 280;
- 每个温度下采用固定的迭代次数Lk = 100n,,n为城市数量;
- 温度衰减系数α = 0.92,即tk+1 = 0.92 * tk;
- 算法停止准则:温度t < 0.1。
3) 新解产生
实验中采用2变换法来产生新解:任选序号u和v (u<v),将u和v及其之间的顺序逆转,即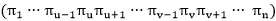 变为
变为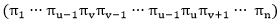 。
。
4) 指标函数
实验中的指标函数设置为城市序列的总距离。指标函数差为新解与原解之间的指标函数差。即有:
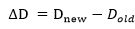
5) 新解接受准则
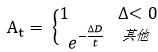
3.程序流程
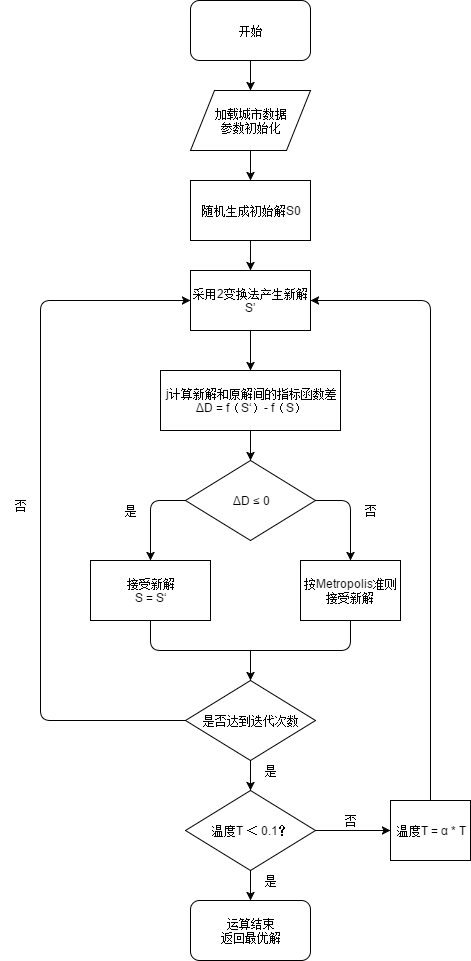
4.核心伪代码
Procedure TSP_USE_SIMULATED_ANNEALING;
begin
LOAD_DATA; { 加载城市数据[(x1, y1), (x2, y2), … , (xn, yn)] }
INITIALIZE; { 初始化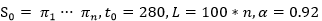 }
}
Repeat
for l := 1 to L do
begin
GENERATE; { 采用2变换法产生新的路径 }
CALCULATE(ΔD); { 计算新路径下的总距离差}
if ACCEPT(t, ΔD) then { 根据Metropolis准则判断是否接受新的路径 }
begin
S_new := S_now; { 更新可能解为当前城市序列 }
end;
end;
t := t * α; { 衰减函数 }
until t < 0.1 { 停止准则为温度小于0.1 }
End;
5.代码运行及测试
实验中采用两个数据集来测试模拟退火算法在TSP问题上的表现。第一个数据集CITY-52来源于网上,包含52个城市,每个城市i均由整数型坐标来表示。第二个数据集为CITY-10,是使用0-1均匀分布随机函数生成的10个浮点型城市数据。相关实验参数设置如2部分所述。
实验中利用模拟退火算法分别计算在CITY-52和CITY-10上的TSP求解,得到城市序列总距离于温度迭代次数的曲线关系分别如下所示。

图 1 城市总距离d与温度迭代次数t的曲线(左图为CITY-52,右图为CITY-10)
从图中可以看出,在CITY-52上,模拟退火算法仅经过25次左右温度迭代便收敛到最优解,而在CITY-10上,由于城市数据为浮点型数据,且满足0-1均匀分布,城市之间距离差异小,因此在搜索过程中波动较大,但是在经过100多次温度迭代后,算法也收敛到了最优解。
实验表明无论在大值整数型数据还是在0-1浮点型数据下,模拟退火算法都能够在TSP问题上收敛,证明了算法的有效性和先进性。而且经过多次测试,算法在CITY-52均可以收敛到全局最优解7544.3659,对应最优序列为:[10 50 32 42 9 8 7 40 18 44 31 48 0 21 30 17 2 16 20 41 6 1 29 22 19 49 28 15 45 43 33 34 35 38 39 36 37 47 23 4 14 5 3 24 11 27 26 25 46 12 13 51]。
6.结论
旅行商问题(TSP)可利用模拟退火算法、遗传算法、蚁群算法等多种算法求解,在本实验中,我们利用模拟退火算法来求解TSP问题。我们通过实验分析以及权衡时间和质量等因素确定了模拟退火算法的初始算法,并采用2变换法来产生新解。实验测试了算法在CITY-52以及CITY-10两个数据集上的表现情况,在少数次温度迭代之后,算法便收敛到了全局最优解,证明了模拟退火算法在TSP问题上的有效性和先进性。
实验时为了便于实现和观察,将指标函数差设为城市序列的总距离差,但是由于2变换法的对称性,指标函数差可以简化为变换点距离之差,从而提高算法运行时的计算速度。此外,实验的初始参数还可以根据城市数据类型进行相应的量级变换,这些都能够进一步得提高模拟退火算法表现。
7.源码
import numpy as np import matplotlib.pyplot as plt # 随机生成nums个城市数据 def city_generator(nums): from numpy import random citys = [] N = 0 while N < nums: x = random.randn() y = random.randn() if [x, y] not in citys: citys.append([x, y]) N = N + 1 return np.array(citys) # CITY-52,包含52个城市 def init_city52(): citys = np.array([[565.0, 575.0], [25.0, 185.0], [345.0, 750.0], [945.0, 685.0], [845.0, 655.0], [880.0, 660.0], [25.0, 230.0], [525.0, 1000.0], [580.0, 1175.0], [650.0, 1130.0], [1605.0, 620.0], [1220.0, 580.0], [1465.0, 200.0], [1530.0, 5.0], [845.0, 680.0], [725.0, 370.0], [145.0, 665.0], [415.0, 635.0], [510.0, 875.0], [560.0, 365.0], [300.0, 465.0], [520.0, 585.0], [480.0, 415.0], [835.0, 625.0], [975.0, 580.0], [1215.0, 245.0], [1320.0, 315.0], [1250.0, 400.0], [660.0, 180.0], [410.0, 250.0], [420.0, 555.0], [575.0, 665.0], [1150.0, 1160.0], [700.0, 580.0], [685.0, 595.0], [685.0, 610.0], [770.0, 610.0], [795.0, 645.0], [720.0, 635.0], [760.0, 650.0], [475.0, 960.0], [95.0, 260.0], [875.0, 920.0], [700.0, 500.0], [555.0, 815.0], [830.0, 485.0], [1170.0, 65.0], [830.0, 610.0], [605.0, 625.0], [595.0, 360.0], [1340.0, 725.0], [1740.0, 245.0]]) return citys class TSP: def __init__(self): self._init_citys() self._init_dist() self._init_params() ## 初始化参数 def _init_params(self): # 初始温度 self.T = 280 # 每个温度下的迭代次数 self.L = 100 * self.n # 温度下降缩减因子 self.alpha = 0.92 # 初始状态 self.S = np.arange(self.n) # 初始化城市 def _init_citys(self): self.citys = init_city52() # self.citys = city_generator(30) self.n = self.citys.shape[0] # 得到距离矩阵的函数 def _init_dist(self): self.Dist = np.zeros((self.n, self.n)) for i in range(self.n): for j in range(i, self.n): self.Dist[i][j] = self.Dist[j][i] = np.linalg.norm(self.citys[i] - self.citys[j]) # 计算在状态下S的能量 def energy(self, S): sum = 0 for i in range(self.n-1): sum = sum + self.Dist[S[i]][S[i+1]] sum = sum + self.Dist[S[self.n-1]][S[0]] return sum # 从状态S的邻域中随机选择 def neighbors(self, S): S_neibor = np.copy(S) u = np.random.randint(0, self.n) v = np.random.randint(0, self.n) while u == v: v = np.random.randint(0, self.n) S_neibor[u], S_neibor[v] = S_neibor[v], S_neibor[u] return S_neibor # 从状态S的邻域中随机选择 def neighbors2(self, S): S_neibor = np.copy(S) u = np.random.randint(0, self.n) v = np.random.randint(0, self.n) if u > v: u, v = v, u while u == v: v = np.random.randint(0, self.n) temp = S_neibor[u:v] S_neibor[u:v] = temp[::-1] return S_neibor # 模拟退火搜索过程 def search(self): Ts = [] Es = [] while self.T >= 0.1: print('search on T:{}'.format(self.T)) for i in range(self.L): E_pre = self.energy(self.S) S_now = self.neighbors2(self.S) E_now = self.energy(S_now) if (E_now < E_pre) or (np.exp((E_pre - E_now) / self.T) >= np.random.rand()): self.S = S_now Ts.append(self.T) E_now = self.energy(self.S) Es.append(E_now) print(E_now) # 判断是否达到终止状态 self.T = self.T * self.alpha print(self.S) print('finished ') return Ts, Es if __name__ == '__main__': tsp = TSP() Ts, Es = tsp.search() plt.plot(Es) plt.show()