Leetcode-5148 Binary Tree Coloring Game(二叉树着色游戏)

 这题还是有点意思的，因为只能从第一个染色节点开始拓展，所以作为后手的B，一定是将A的第一个染色节点的父亲或者两个儿子染色，堵住A的路，这样才有可能获胜。

所以B占据的区域要么是除A占据的子树以外的部分，要么就是A的第一个染色节点的左子树或者右子树，只有这三种情况.

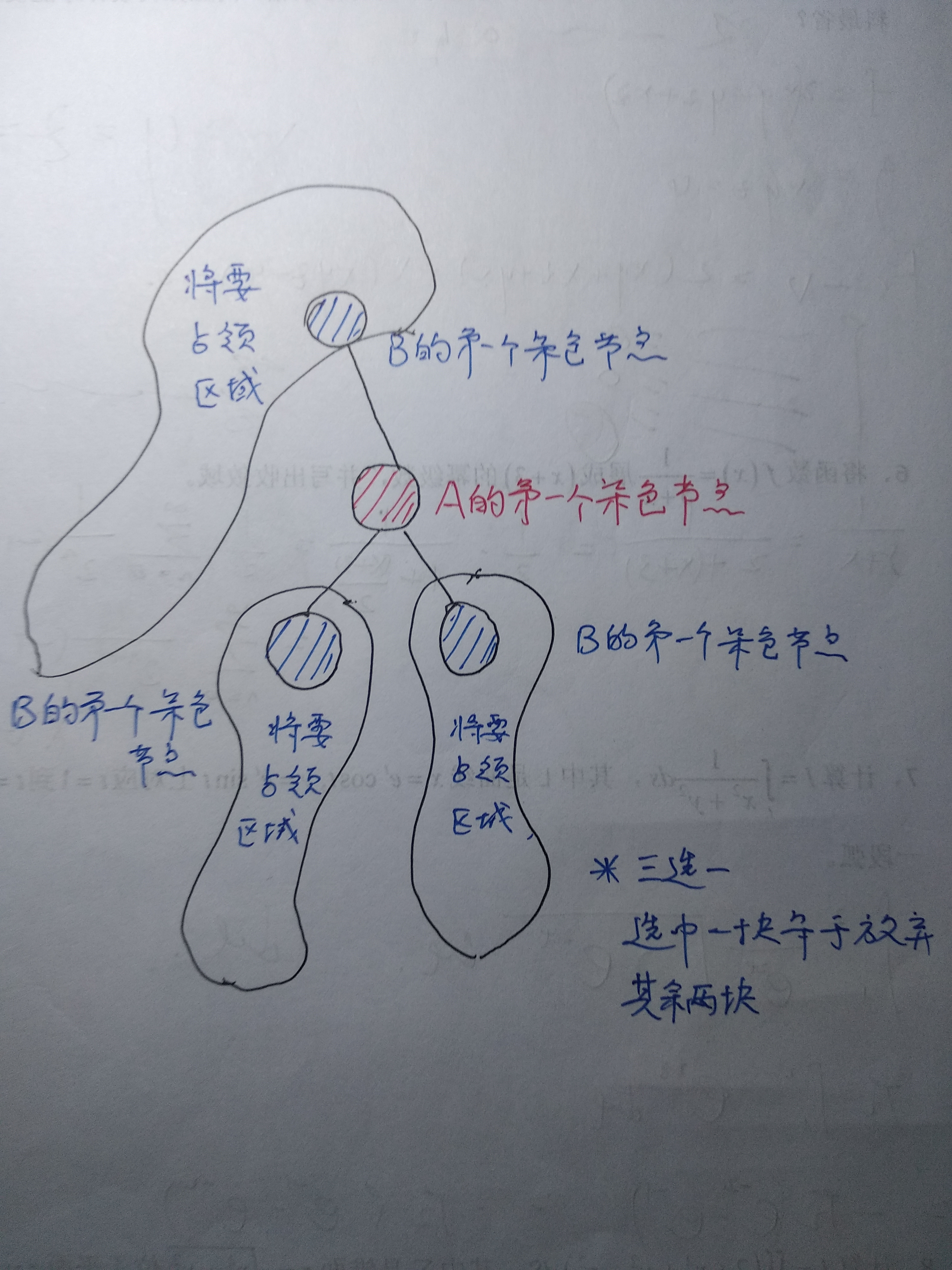
所以我们计算一下A的第一个染色节点的左子树和右子树的节点个数，就可以得知

1、左子树的节点个数，

2、右子树的节点个数

3、A的第一个染色节点的子树的节点个数

4、除A的第一个染色节点的子树的节点其余节点的个数

如果

1、左子树的节点个数比其余地方的节点个数多

2、右子树的节点个数比其余地方的节点个数多

3、彻底放弃A的第一个染色节点的子树，其他区域的节点个数比A的第一个染色节点的子树的节点个数多

就能获胜，除此以外都不能获胜.

class Solution
{
    public:
        int f(TreeNode* root)
        {
            if(!root) return 0;
            return f(root->left)+f(root->right)+1;
        }
        TreeNode* preorder(TreeNode *root,int x)
        {
            if(!root) return NULL;
            if(root->val==x)
                return root;
            TreeNode *t1 = preorder(root->left,x);
            TreeNode *t2 = preorder(root->right,x);
            if(t1) return t1;
            else if(t2) return t2;
            return NULL;
        }
        bool btreeGameWinningMove(TreeNode* root, int n, int x)
        {
            TreeNode* t = preorder(root,x);
            int k1 = f(t->left);
            int k2 = f(t->right);
            //k1 > n-k1 || k2 > n-k2 || n-k1-k2-1 > k1+k2+1 分别对应题解中三种情况
            if(max(2*k1,2*k2)>n || n>2*(k1+k2+1))
                return true;
            return false;
        }
};