[论文阅读笔记] RoSANE, Robust and scalable attributed network embedding for sparse networks

[论文阅读笔记] RoSANE: Robust and scalable attributed network embedding for sparse networks

---

本文结构

1. 解决问题
2. 主要贡献
3. 算法原理
4. 参考文献

---

(1) 解决问题

• 大多现有的ANE (attributed network embedding) 算法没有考虑由稀疏网络引起的问题（仍然利用边来处理节点属性，而稀疏网络中的边非常少，可以提供的信息有限）。
• 现有ANE算法的可扩展性问题（一些属性网络表征框架仍然存在相对于节点数为平方级别或者三次方级别的时间复杂度）。
• 有些ANE算法对于不同网络的鲁棒性比较低，保证算法在不同网络上参数比较好调整才能更好地应用于到规模网络（某些算法的参数需要网格寻优，开销非常大。难以适应现实场景）。

---

(2) 主要贡献

Contribution 1： 详细讨论了不同类别算法应对稀疏网络存在的问题。

ANE算法大致分为四类：

• 基于凸优化 (矩阵分解): 最终要求一个矩阵分解操作，这是非常耗时的，使得算法不能适用于大规模网络。
• 基于图卷积网络: GCN、graphSAGE 依赖于边来聚合节点属性，可能在稀疏网络中的性能比较低。GRCN融合节点属性相似度到节点的邻接矩阵中，其次利用GCN、graphSAGE类似的方法来做网络表征。然而节点属性相似度的精确计算需要节点数三次方的复杂度。
• 基于深度神经网络：虽然能够很好地挖掘非线性关系，然而计算复杂度是比较高的。
• 基于随机游走的方法：在一个边比较稀疏的网络上，随机游走能够捕获到的节点关系少之又少。

Contribution 2： 提出一种新颖的ANE方法RoSANE，即构造并且融合拓扑结构和属性的转移矩阵，使用转移概率矩阵来指导图上的随机游走，相当于重构了一个结合节点拓扑结构和属性信息的稠密网络且在该网络基础上做网络表征。

---

(3) 算法原理

RoSANE算法主要的框架如下图所示： 假设有多个信息源 S，所提方法为每个信息源构造节点转移概率矩阵T ，并且将多个节点转移概率矩阵融合成一个统一的节点转移概率矩阵（相当于融合多方信息重构了一个更加稠密的网络），从而利用该转移概率矩阵在图上实现随机游走，最后利用表征模型Skip-Gram进行节点向量训练。

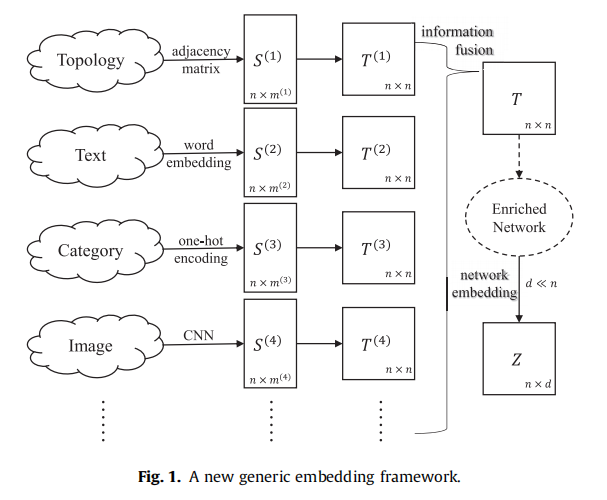
以下就使用拓扑信息和节点属性信息两方信息来对上述框架细节进行阐述：

• 第一步，拓扑信息转移概率矩阵构造： 如下公式所示，即相当于对边权矩阵做一个简单的行归一化来得到拓扑信息转移概率矩阵，边权越大则转移概率越大。

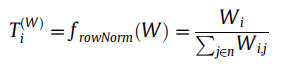
• 第二步，属性信息转移概率矩阵构造： 为了避免计算网络中所有节点对的属性相似度（完整计算的话节点属性相似度矩阵会有n平方个非零元素），算法使用球树K近邻技术来快速构造每个节点属性上最相似的k个邻居（这样节点属性相似度矩阵只会有 n x k 个非零元素），k近邻采用余弦函数来衡量节点属性向量的矩阵。得到仅有 n x k 个非零元素的属性相似度矩阵之后，进行矩阵行归一化即可得到节点属性信息转移概率矩阵，属性相似度越大则转移概率越大。

• 第三步，信息融合（融合节点拓扑转移矩阵和属性转移矩阵构造最终转移概率矩阵T）： 如下列公式所示，T(W) 和 T(X) 分别为节点拓扑转移矩阵以及节点属性转移矩阵。以下公式所表达的意思是，如果某个节点在拓扑上与其他节点都没有连边的话（孤立点），则按属性转移概率矩阵进行节点跳转。否则综合考虑拓扑转移矩阵以及属性转移矩阵（加权求和）。

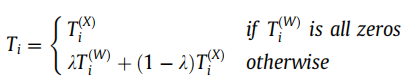
• 第四步，按第三步训练Skip-Gram学习节点表示向量（不再赘述）。

---

(4) 参考文献

Hou, Chengbin, Shan He, and Ke Tang. "RoSANE: Robust and scalable attributed network embedding for sparse networks." Neurocomputing 409 (2020): 231-243.

---