这篇博客大部分在写我的错解……明明很简单的一道题,知道正解后10分钟AC,然而几个错解打的想死……
错解1 WA40:
鬼知道这40分哪来的……这也是考试最后很无奈地交上去的代码,最后剩20分钟时发现这是错的,最后剩7分钟想出错解2,我也是醉了……
先说一下思路吧,首先跑一边Dijkstra记录1到n的最短路,那么必经点一定在这条路径上。然后怎么搞呢?以下纯属YY,从n开始向回扫,遇到第一个dis不是INF的停止……鬼知道我咋想的,其实是为了QJ样例。

1 tem=n; 2 while(tem!=1) 3 { 4 if(tem!=n)ans.push_back(tem); 5 if(dis[tem]!=INF)break; 6 nex[u(pre[tem])]=tem; 7 tem=u(pre[tem]); 8 }
错解2 WA90:
只能说测试点有点水啊,接着上面说,找到了最短路,必经点在这条路径上,但是这条路径上的点不一定都是必经点,什么情况下点i不是毕竟点呢?我们可以发现,当i被一条其他边覆盖时,i一定不是必经点,这里的覆盖不包括连接:如图节点3就被覆盖,而节点2,4就不算被覆盖,知道了这个结论,我们就可以求出来答案了,具体怎么做呢?首先tarjan缩边双,记录每个边双在这条路径上的端点,那么我们就可一求出答案了。但是难点就在于边双的端点记录起来比较难以实现。以上是正确结论,以下纯属YY:
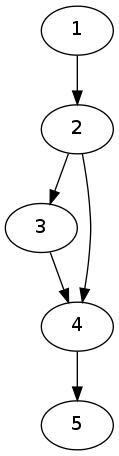
可以发现端点一定是和桥连着的,所以我们连索点都省了,只需要记录这条路径,然后tarjan求割边,枚举边,将即在这条路径上又是桥的边的端点(1,n除外)扔入vector,最后排序去重即可。
显然以上YY是错的(其实可能并不显然),直接上数据好了:

如图,显然4是必经点,但是4没有与割边连接,只能说测试点太水了,居然有90分……

1 #include<algorithm> 2 #include<iostream> 3 #include<cstring> 4 #include<cstdio> 5 #include<queue> 6 #define int long long 7 #define MAXN 2000010 8 #define MP(a,b) make_pair(a,b) 9 #define ma(x) memset(x,0,sizeof(x)) 10 #define min(a,b) ((a)<(b)?(a):(b)) 11 using namespace std; 12 const int L=1<<20|1; 13 char buffer[L],*S,*T; 14 #define getchar() ((S==T&&(T=(S=buffer)+fread(buffer,1,L,stdin),S==T))?EOF:*S++) 15 struct edge 16 { 17 int u,v,nxt; 18 #define u(x) ed[x].u 19 #define v(x) ed[x].v 20 #define n(x) ed[x].nxt 21 }ed[MAXN*2]; 22 int first[MAXN],num_e=1; 23 #define f(x) first[x] 24 int TT,n,m; 25 int dfn[MAXN],low[MAXN],cnt; 26 bool bridge[MAXN*2]; 27 void tarjan(int x,int edg,int fa) 28 { 29 dfn[x]=low[x]=++cnt; 30 for(int i=f(x);i;i=n(i)) 31 if(!dfn[v(i)]) 32 { 33 tarjan(v(i),i,x),low[x]=min(low[x],low[v(i)]); 34 if(low[v(i)]>dfn[x]) 35 bridge[i]=bridge[i^1]=1; 36 } 37 else if(v(i)!=fa&&(i^1)!=edg)low[x]=min(low[x],dfn[v(i)]); 38 } 39 int dis[MAXN];bool v[MAXN]; 40 int pre2[MAXN]; 41 void dist2(int st) 42 { 43 for(int i=0;i<=n;i++)dis[i]=0x7ffffffffff,v[i]=0; 44 dis[st]=0; 45 priority_queue<pair<int,int> >q; 46 q.push(MP(0,st)); 47 while(!q.empty()) 48 { 49 int x=q.top().second;q.pop(); 50 if(v[x])continue;v[x]=1; 51 for(int i=f(x);i;i=n(i)) 52 if(dis[v(i)]>dis[x]+1) 53 { 54 dis[v(i)]=dis[x]+1; 55 pre2[v(i)]=i; 56 q.push(MP(-dis[v(i)],v(i))); 57 } 58 } 59 } 60 bool is[MAXN*2]; 61 int ans[MAXN*4],an; 62 inline void add(int u,int v); 63 inline int read() 64 { 65 int s=0;char a=getchar(); 66 while(a<'0'||a>'9')a=getchar(); 67 while(a>='0'&&a<='9'){s=s*10+a-'0';a=getchar();} 68 return s; 69 } 70 signed main() 71 { 72 // freopen("in.txt","r",stdin); 73 // freopen("0.out","w",stdout); 74 75 cin>>TT; 76 while(TT--) 77 { 78 79 cnt=0;num_e=1;ma(ans),an=0; 80 n=read(),m=read(); 81 for(int i=0;i<=n;i++)first[i]=is[i]=pre2[i]=low[i]=dfn[i]=0; 82 ma(bridge);ma(is); 83 int ta,tb; 84 for(int i=1;i<=m;i++) 85 { 86 ta=read(),tb=read(); 87 add(ta,tb),add(tb,ta); 88 } 89 dist2(1); 90 int tem=n; 91 while(tem!=1) 92 { 93 is[pre2[tem]]=is[pre2[tem]^1]=1; 94 tem=u(pre2[tem]); 95 } 96 for(int i=1;i<=n;i++) 97 if(!dfn[i])tarjan(i,0,0); 98 for(int i=2;i<=num_e;i+=2) 99 if(bridge[i]&&is[i]) 100 { 101 if(u(i)!=1&&u(i)!=n)ans[++an]=u(i); 102 if(v(i)!=1&&v(i)!=n)ans[++an]=v(i); 103 } 104 sort(ans+1,ans+an+1); 105 int m=unique(ans+1,ans+an+1)-ans-1; 106 printf("%lld ",m); 107 for(int i=1;i<=m;i++) 108 printf("%lld ",ans[i]); 109 printf(" "); 110 } 111 } 112 inline void add(int u,int v) 113 { 114 ++num_e; 115 u(num_e)=u; 116 v(num_e)=v; 117 n(num_e)=f(u); 118 f(u)=num_e; 119 }
正解:
以上纯属扯淡,其实这个题还是求割点,只要在tarjan是加一句特判就可以了,几乎就是裸的tarjan……
#include<iostream> #include<cstring> #include<cstdio> #define ma(x) memset(x,0,sizeof(x)) #define MAXN 2000010 using namespace std; struct edge { int u,v,nxt; #define u(x) ed[x].u #define v(x) ed[x].v #define n(x) ed[x].nxt }ed[MAXN*2]; int first[MAXN],num_e; #define f(x) first[x] int n,m; int dfn[MAXN],low[MAXN],num,root; bool cut[MAXN]; int stack[MAXN],top; void tarjan(int x) { dfn[x]=low[x]=++num; stack[++top]=x; if(x==root&&!f(x)){return;} int flag=0; for(int i=f(x);i;i=n(i)) if(!dfn[v(i)]) { tarjan(v(i)),low[x]=min(low[x],low[v(i)]); if(low[v(i)]>=dfn[x]&&dfn[v(i)]<=dfn[n]&&dfn[n])//x是割点,如果dfn[v(i)]<=dfn[n]则说明如果要到n必须经过x。 { flag++; if(x!=root||flag>1) cut[x]=1; } } else low[x]=min(low[x],dfn[v(i)]); } int TT; inline int read() { int s=0;char a=getchar(); while(a<'0'||a>'9')a=getchar(); while(a>='0'&&a<='9'){s=s*10+a-'0';a=getchar();} return s; } inline void add(int u,int v) { ++num_e; u(num_e)=u; v(num_e)=v; n(num_e)=f(u); f(u)=num_e; } signed main() { cin>>TT; while(TT--) { ma(first);ma(cut);num=root=top=0;ma(ed);ma(dfn);ma(low); n=read(),m=read(); int ta,tb; for(int i=1;i<=m;i++) { ta=read(),tb=read(); add(ta,tb),add(tb,ta); } for(int i=1;i<=n;i++) if(!dfn[i])root=i,tarjan(i); int nn=0; for(int i=2;i<n;i++) if(cut[i])nn++; printf("%d ",nn); for(int i=2;i<n;i++) if(cut[i])printf("%d ",i); puts(""); } }
