机器学习十讲第七讲

机器学习的优化目标

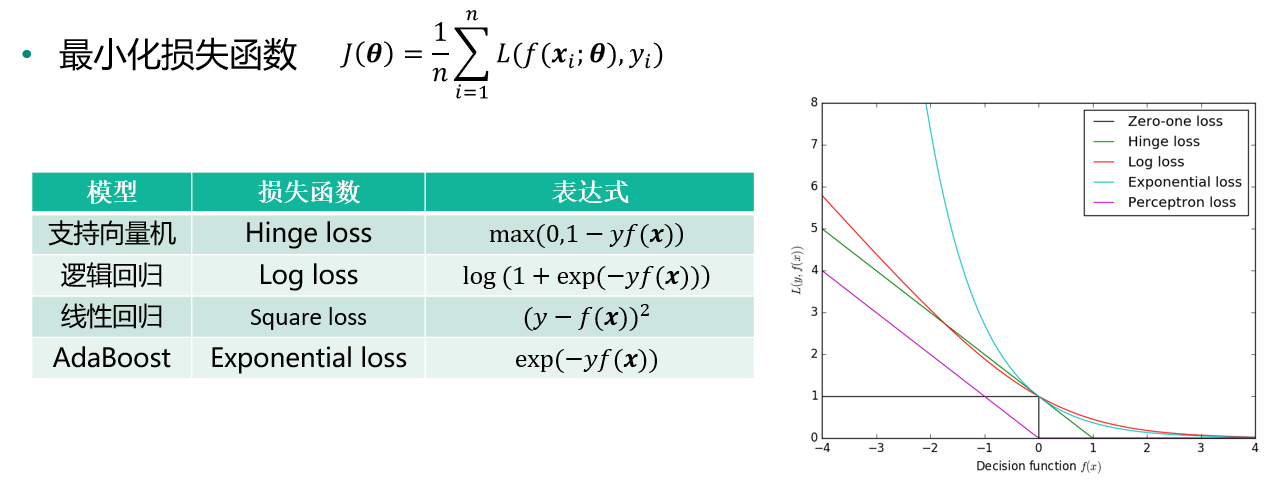
梯度下降

三维示意

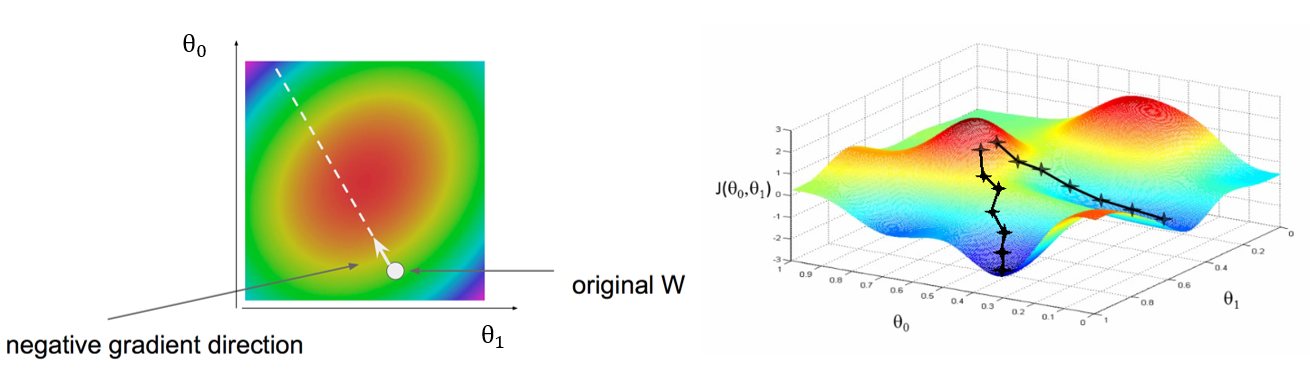
batch 和 mini-batch 梯度下降

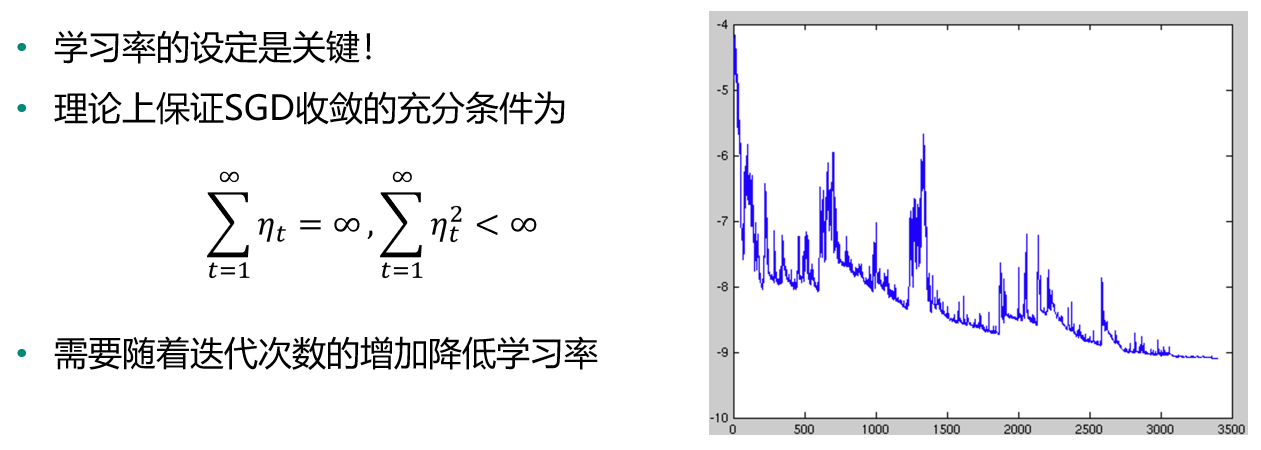
梯度下降SGD

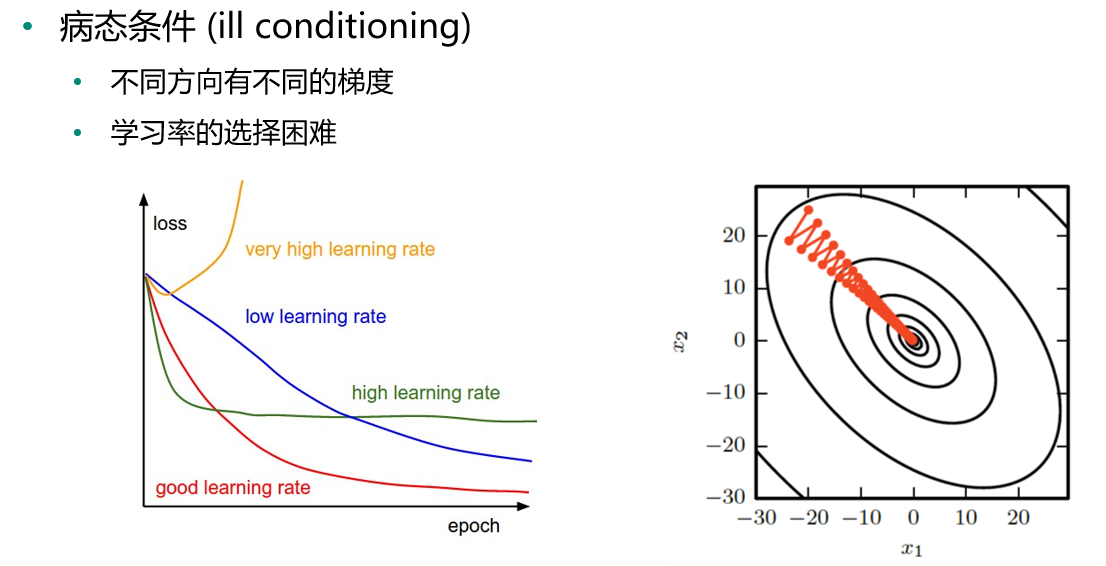
病态条件

局部最小 vs 全局最小

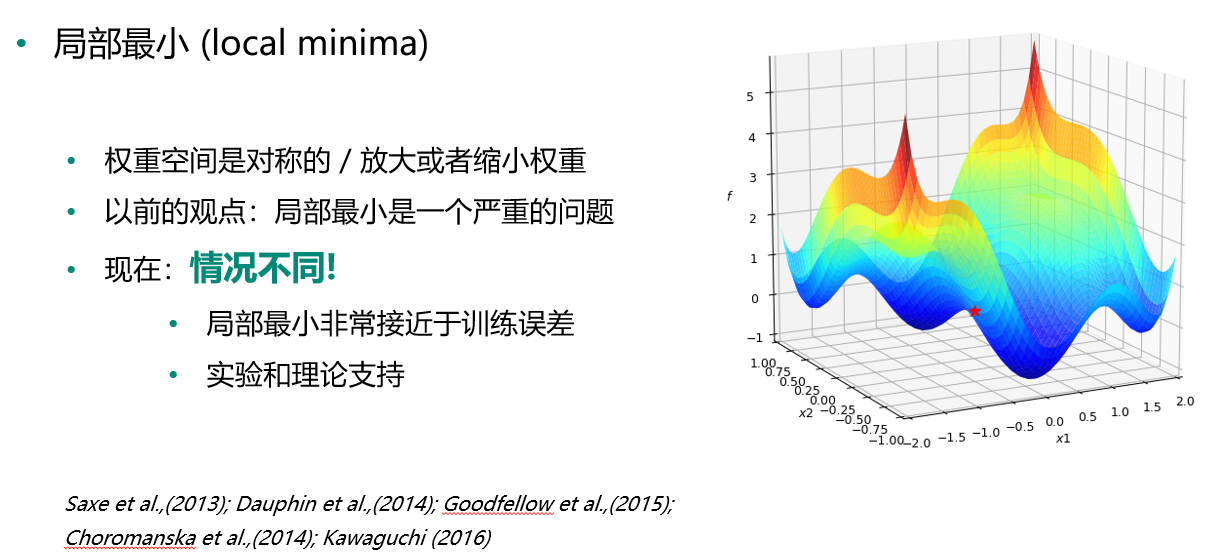
鞍点

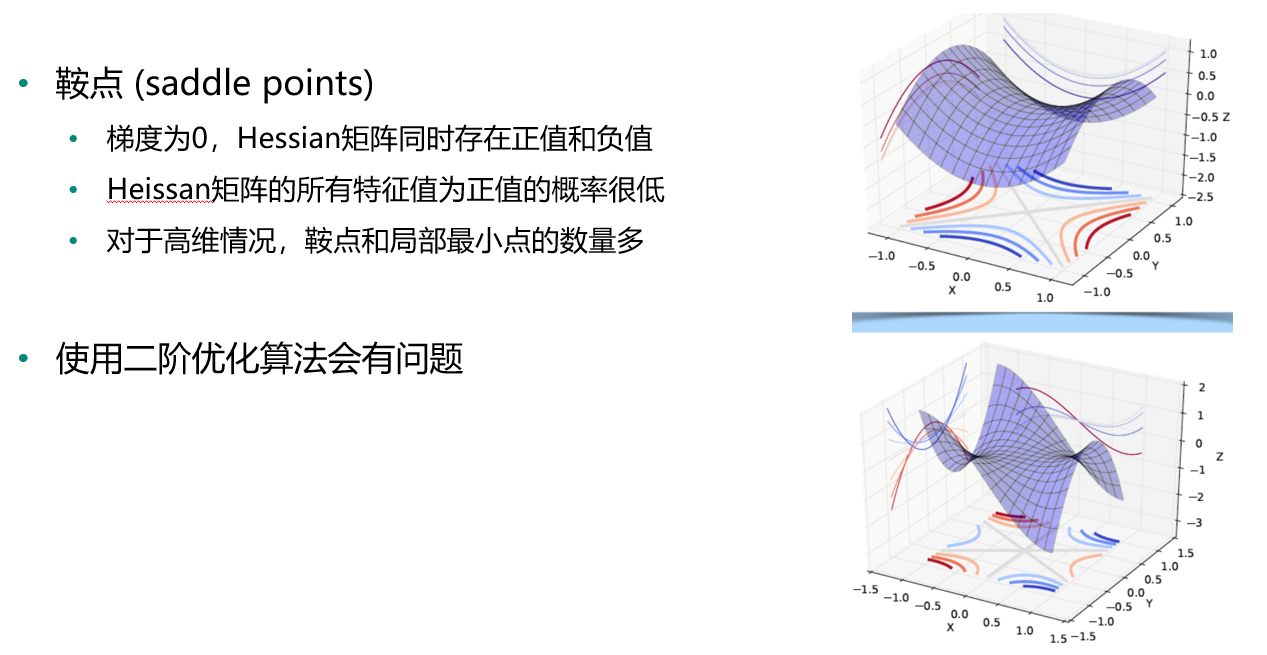
平台

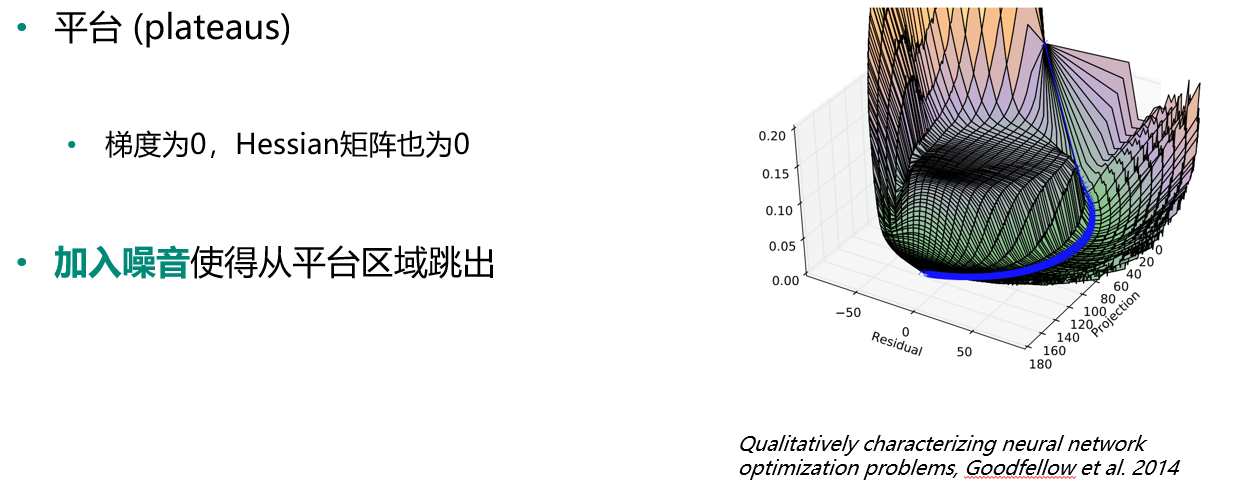
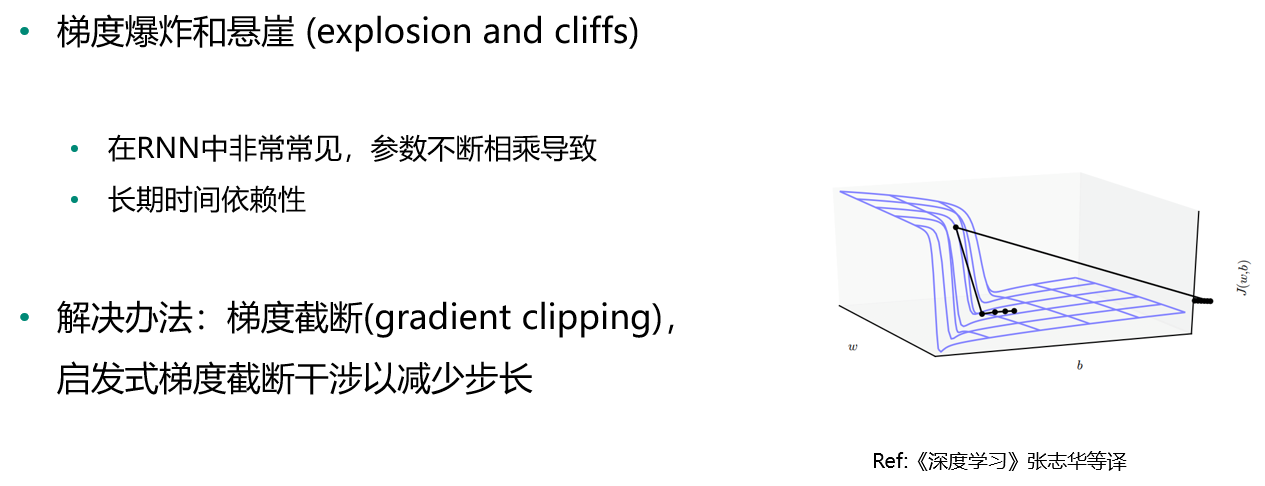
梯度爆炸与悬崖

动量法

Nesterov 动量法

• 受 Nesterov 加速梯度算法 NAG(Nesterov, 1983, 2004) 的启发
• 梯度计算在施加当前速度之后
• 在动量法基础上添加了一个校正因子（correction factor）

AdaGrad

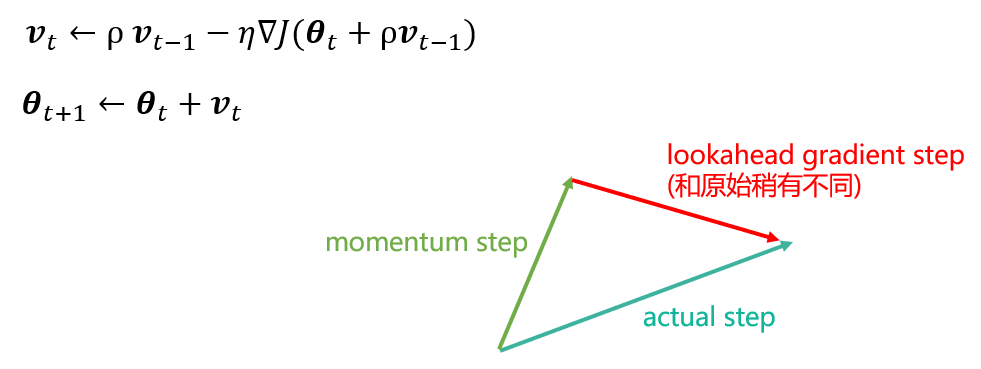
RMSProp

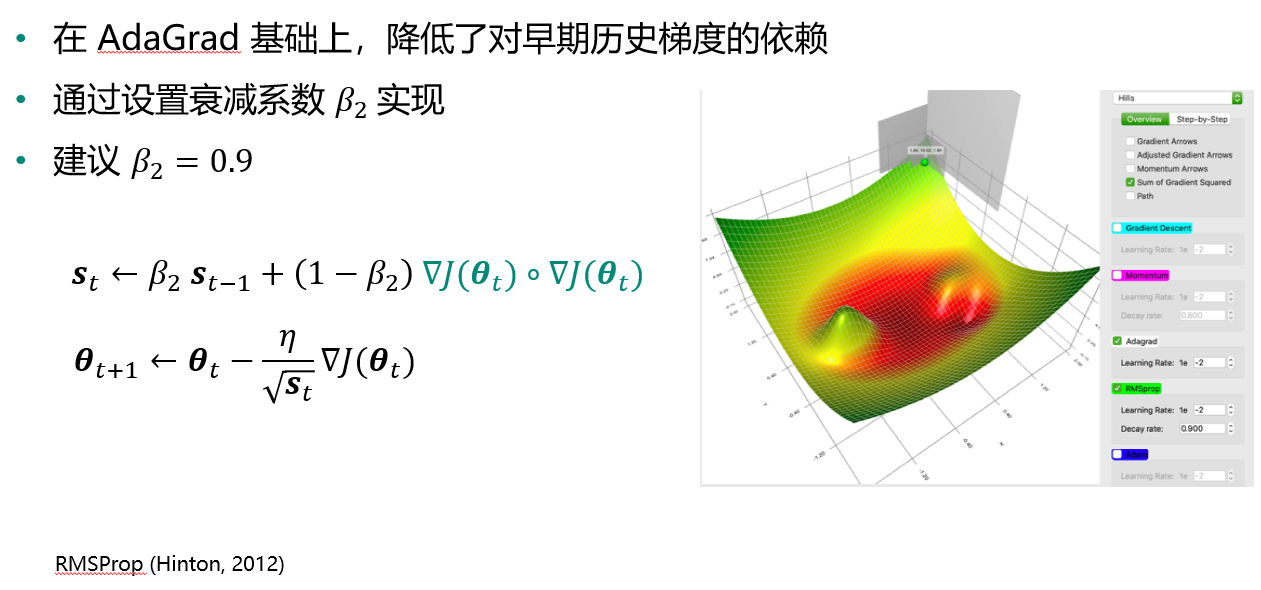
Adam

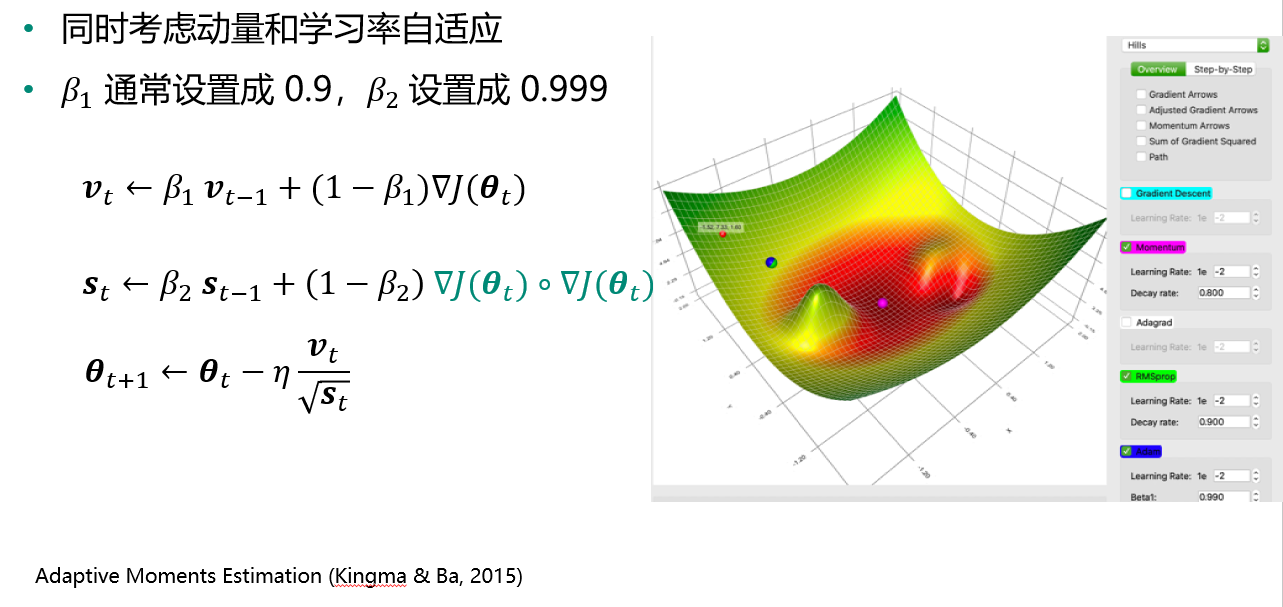
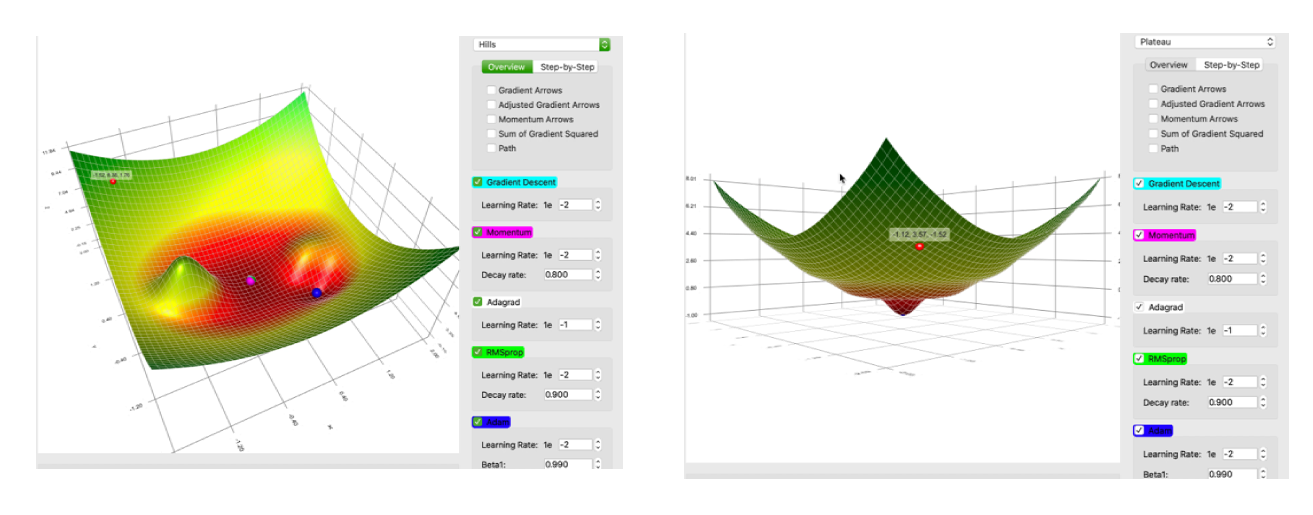
不同一阶优化学习方法的比较

二阶优化方法

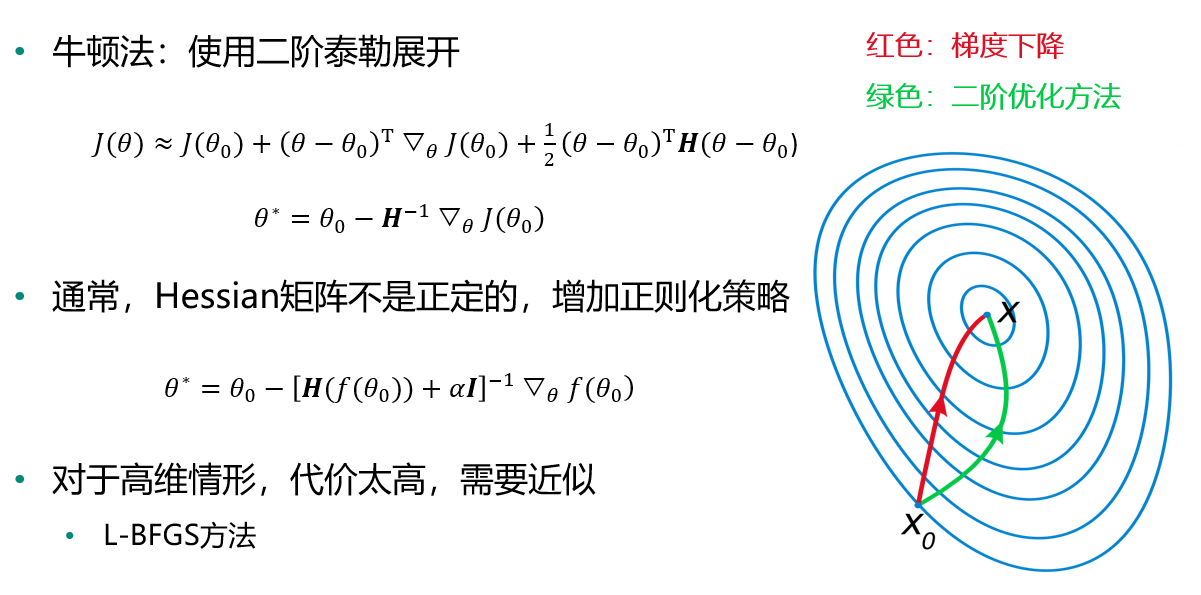
选择哪一种优化方法

• 在大数据场景（样本量大，特征维数大）下，一阶方法最实用（随机梯度）
• 自适应学习率算法族（以RMSProp为代表）表现相当鲁棒
• Adam可能是最佳选择
• 使用者对算法的熟悉程度，以便于调节超参数

实例

Python算法实现与比对：

#先引入算法相关的包，matplotlib用于绘图
import matplotlib.pyplot as plt
import numpy as np

from mpl_toolkits.mplot3d import Axes3D
from matplotlib import animation
from IPython.display import HTML

from autograd import elementwise_grad, value_and_grad,grad
from scipy.optimize import minimize
from scipy import optimize
from collections import defaultdict
from itertools import zip_longest
plt.rcParams['axes.unicode_minus']=False  # 用来正常显示负号
#使用python的匿名函数定义目标函数
f1 = lambda x1,x2 : x1**2 + 0.5*x2**2 #函数定义
f1_grad = value_and_grad(lambda args : f1(*args)) #函数梯度

#梯度下降法
##定义gradient_descent方法对参数进行更新
###func:f1 // func_grad:f1_grad // x0:初始点 // learning_rate:学习率 // max_iteration:最大步数
def gradient_descent(func, func_grad, x0, learning_rate=0.1, max_iteration=20):
    #记录该步如何走（可视化使用）
    path_list = [x0]
    #当前走到哪个位置
    best_x = x0
    step = 0
    while step < max_iteration:
        update = -learning_rate * np.array(func_grad(best_x)[1])
        if(np.linalg.norm(update) < 1e-4):
            break
        best_x = best_x + update
        path_list.append(best_x)
        step = step + 1
    return best_x, np.array(path_list)

#举个例子来讲梯度下降的求解路径可视化
best_x_gd, path_list_gd = gradient_descent(f1,f1_grad,[-4.0,4.0],0.1,30)
path_list_gd

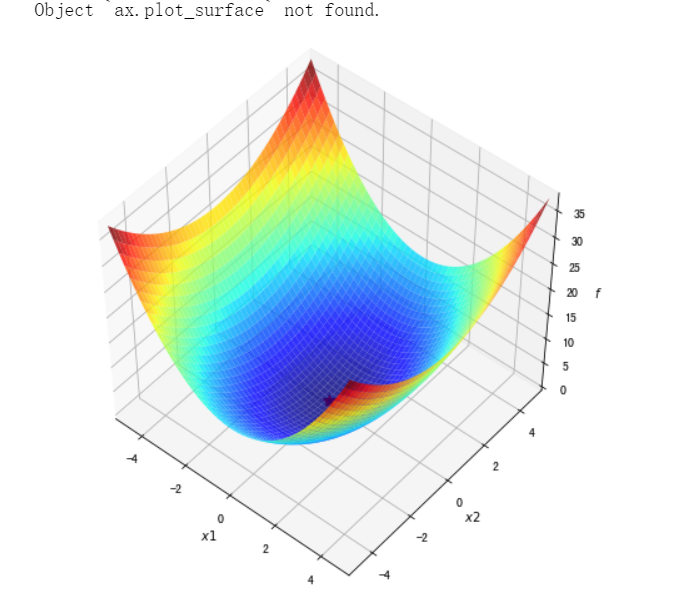
#绘制函数曲面
##先借助np.meshgrid生成网格点坐标矩阵。两个维度上每个维度显示范围为-5到5。对应网格点的函数值保存在z中
x1,x2 = np.meshgrid(np.linspace(-5.0,5.0,50), np.linspace(-5.0,5.0,50))
z = f1(x1,x2 )
minima = np.array([0, 0]) #对于函数f1，我们已知最小点为(0,0)
ax.plot_surface?
##plot_surface函数绘制3D曲面
%matplotlib inline
fig = plt.figure(figsize=(8, 8))
ax = plt.axes(projection='3d', elev=50, azim=-50)

ax.plot_surface(x1,x2, z, alpha=.8, cmap=plt.cm.jet)
ax.plot([minima[0]],[minima[1]],[f1(*minima)], 'r*', markersize=10)

ax.set_xlabel('$x1$')
ax.set_ylabel('$x2$')
ax.set_zlabel('$f$')

ax.set_xlim((-5, 5))
ax.set_ylim((-5, 5))

plt.show()

#绘制等高线和梯度场
##contour方法能够绘制等高线，clabel能够将对应线的高度（函数值）显示出来，这里我们保留两位小数（fmt='%.2f'）。
dz_dx1 = elementwise_grad(f1, argnum=0)(x1, x2)
dz_dx2 = elementwise_grad(f1, argnum=1)(x1, x2)
fig, ax = plt.subplots(figsize=(6, 6))

contour = ax.contour(x1, x2, z,levels=20,cmap=plt.cm.jet)
ax.clabel(contour,fontsize=10,colors='k',fmt='%.2f')
ax.plot(*minima, 'r*', markersize=18)

ax.set_xlabel('$x1$')
ax.set_ylabel('$x2$')

ax.set_xlim((-5, 5))
ax.set_ylim((-5, 5))

plt.show()