
题目大意
给$n!$个$n$的排列,按字典序从小到大连成一条序列,例如$3$的情况为:$[1,2,3, 1,3,2, 2,1,3 ,2,3,1 ,3,1,2 ,3,2,1]$,问其中长度为$n$,且和为$sum=n imes (n+1)/2$的序列有多少个?
试题分析
对于合理的序列有两种情况,第一种是就是排列的,第二种就是前面$k$个与后面的$n-k$的一块组成。
对于第一种情况,答案只要$n$个,所以我们只考虑第二种情况。
当$n=3$时,$n imes n!=3! imes 3 ext{=}18$
而直接生成的序列为$[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]$
而我们思考$next\_permutatin$是怎么判断下一个排列的,假设某一个序列长度为$n$,最长的递减的后缀长度$k$,那么它的下一个排列是这样产生的:那么它的下一个排列是这样产生的:与后$k$个数中比整个序列的第$n-k$个数大且最小的那个交换,然后将后$k$个数按从小到大排序。
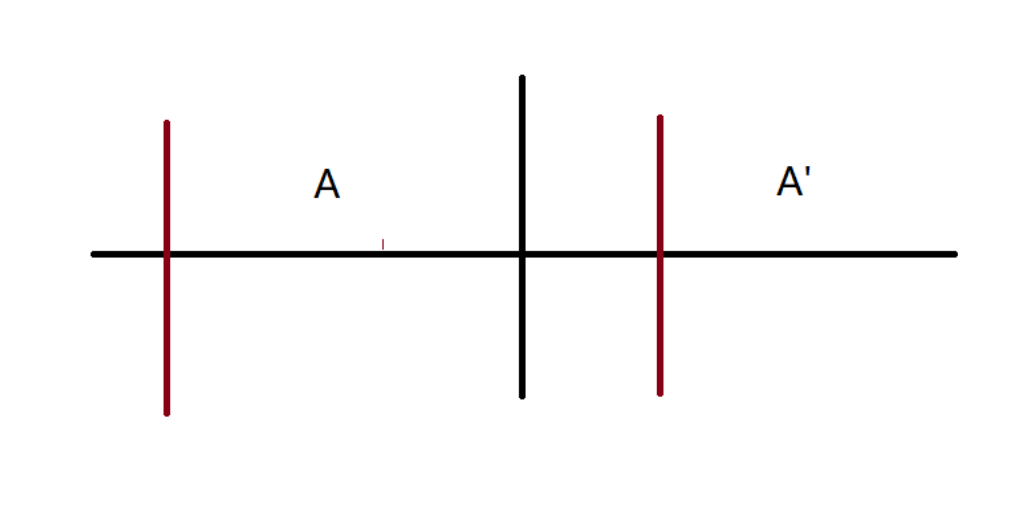
如图所示,若想要成为第二种情况,则$A$集合需等于$A’$集合。
而这时我们能确定$A$当前的一定不是递减的,所以问题可以转换成排除法当前序列末尾$k$个是按序递减的情况数。
举个例子:
$k=1$时,排除$[3,1,3],[2,2,1],[3,2,3],[1,3,1].[2,3,2]$
$k=2$时,排除$[(3,2),2],[(3,1),3]$
所以说我们现在只要求不行的方案数即可。
只要确定了前$k-x$个数,那么后面关于$x$的递减顺序是一定的。
所以当$k=x$时,排除方案数为$A_n^k$,但是最后一个是没有连接的,所以要$-1$,即为$A_n^k-1$
所以总方案数为$n imes n!-(n-1) - sum_{k=1}^{n-1} (frac{n!}{k!}-1)$.
整理的$n imes n!-sum_{k=1}^{n-1} frac{n!}{k!}$

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> #define int long long #define mod 998244353 using namespace std; inline int read() { int f=1,ans=0;char c; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){ans=ans*10+c-'0';c=getchar();} return ans*f; } const int N=2000001; int ans,n,fac[N],f[N]; signed main(){ n=read();fac[0]=1; for(int i=1;i<=n;i++) fac[i]=fac[i-1]*i,fac[i]%=mod; f[n]=1; for(int i=n-1;i>=1;i--) f[i]=f[i+1]*(i+1),f[i]%=mod; ans=n*fac[n]; for(int i=1;i<n;i++) ans=((ans-f[i])%mod+mod)%mod; printf("%d ",ans); }
