试题分析
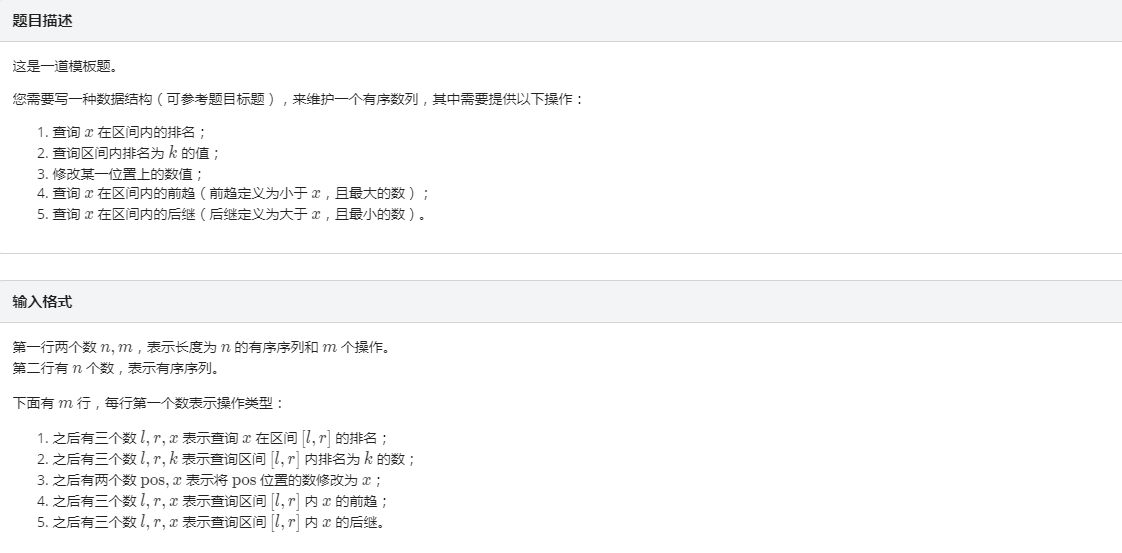
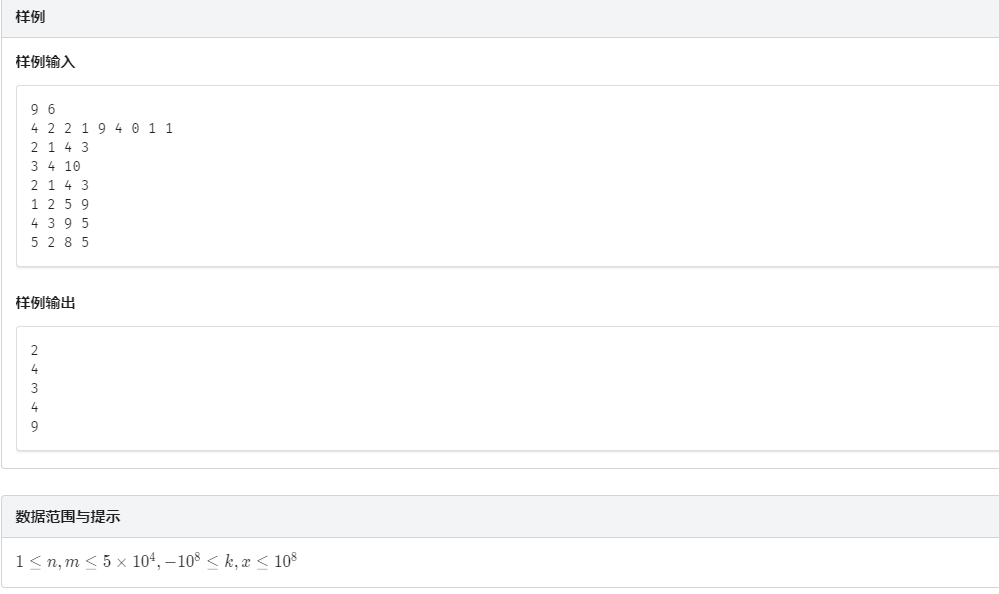
一个十分裸的树套树板子(这也是一个板子),线段树中套平衡树($Treap$)
主要就有一个不是平凡操作的,就是处理第$2$个操作时,因为其他操作确保每次复杂度在$O(log^2 n)$,而$2$操作无法快速在$Treap$中找到,所以就可以去二分一个值,用$1$操作判断即可,单次操作时间复杂度$O(log^3 n)$。并且在$Treap$中查找的排名$x$是小于$x$的最大排名,这样才能保证最后只算一次$x$

#include<iostream> #include<cstring> #include<cstdio> #include<algorithm> #include<ctime> using namespace std; inline int read(){ int f=1,ans=0;char c=getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){ans=ans*10+c-'0';c=getchar();} return f*ans; } const int N=500001; int tot,root[N<<4]; int n,m,val[N]; struct node{ int l,r,cnt,size,rnk,num; }tr[N<<4]; struct Treap{ void update(int k){tr[k].size=tr[k].cnt;tr[k].size+=tr[tr[k].l].size,tr[k].size+=tr[tr[k].r].size;} void zag(int &k){ int tp=tr[k].l; tr[k].l=tr[tp].r; tr[tp].r=k; tr[tp].size=tr[k].size; update(k);k=tp; return; } void zig(int &k){ int tp=tr[k].r; tr[k].r=tr[tp].l; tr[tp].l=k; tr[tp].size=tr[k].size; update(k);k=tp; return; } void insert(int x,int &k){ if(k==0){ k=++tot; tr[k].size=tr[k].cnt=1;tr[k].num=x; tr[k].rnk=rand(); return; } tr[k].size++; if(x==tr[k].num){tr[k].cnt++;return;} if(x<tr[k].num){ insert(x,tr[k].l); if(tr[tr[k].l].rnk<tr[k].rnk) zag(k); }else{ insert(x,tr[k].r); if(tr[tr[k].r].rnk<tr[k].rnk) zig(k); }return; } void del(int x,int &k){ if(x==tr[k].num){ if(tr[k].cnt>1){tr[k].cnt--,tr[k].size--;return;} if(tr[k].l*tr[k].r==0){k=tr[k].l+tr[k].r;return;} if(tr[tr[k].l].rnk<tr[tr[k].r].rnk){zag(k);del(x,k);} else{zig(k);del(x,k);} return; } tr[k].size--; if(x<tr[k].num) del(x,tr[k].l); else del(x,tr[k].r); return; } int qrnk(int x,int k){ if(k==0) return 0; if(tr[k].num==x) return tr[tr[k].l].size; if(x<tr[k].num) return qrnk(x,tr[k].l); return tr[tr[k].l].size+tr[k].cnt+qrnk(x,tr[k].r); } int qpre(int x,int k){ if(k==0) return -2147483647; if(x<=tr[k].num) return qpre(x,tr[k].l); return max(tr[k].num,qpre(x,tr[k].r)); } int qnex(int x,int k){ if(k==0) return 2147483647; if(x>=tr[k].num) return qnex(x,tr[k].r); return min(tr[k].num,qnex(x,tr[k].l)); } }treap; struct Segment_tree{ void build(int k,int l,int r){ for(int i=l;i<=r;i++) treap.insert(val[i],root[k]); if(l==r) return; int mid=l+r>>1; build(k<<1,l,mid),build(k<<1|1,mid+1,r); return; } void change(int k,int l,int r,int x,int y,int w){ treap.del(val[x],root[k]); treap.insert(w,root[k]); if(l==r) return; int mid=l+r>>1; if(x<=mid) change(k<<1,l,mid,x,y,w); if(mid<y) change(k<<1|1,mid+1,r,x,y,w); return; } int qrnk(int k,int l,int r,int x,int y,int val){ if(x<=l&&r<=y) return treap.qrnk(val,root[k]); int mid=l+r>>1,res=0; if(x<=mid) res+=qrnk(k<<1,l,mid,x,y,val); if(mid<y) res+=qrnk(k<<1|1,mid+1,r,x,y,val); return res; } int qpre(int k,int l,int r,int x,int y,int w){ if(x<=l&&r<=y) return treap.qpre(w,root[k]); int res=-2147483647,mid=l+r>>1; if(x<=mid) res=max(res,qpre(k<<1,l,mid,x,y,w)); if(mid<y) res=max(res,qpre(k<<1|1,mid+1,r,x,y,w)); return res; } int qnex(int k,int l,int r,int x,int y,int w){ if(x<=l&&r<=y) return treap.qnex(w,root[k]); int res=2147483647,mid=l+r>>1; if(x<=mid) res=min(res,qnex(k<<1,l,mid,x,y,w)); if(mid<y) res=min(res,qnex(k<<1|1,mid+1,r,x,y,w)); return res; } int qkth(int le,int ri,int kth){ int l=0,r=1e8,maxn=-2147483647; while(l<=r){ int mid=l+r>>1; if(qrnk(1,1,n,le,ri,mid)+1<=kth){l=mid+1,maxn=max(maxn,mid);} else r=mid-1; }return maxn; } }segment; int main(){ srand(time(0)); n=read(),m=read(); for(int i=1;i<=n;i++) val[i]=read(); segment.build(1,1,n); for(int i=1;i<=m;i++){ int opt=read(),l=read(),r=read(); if(opt==1){ int k=read(); printf("%d ",segment.qrnk(1,1,n,l,r,k)+1); } if(opt==2){ int k=read(); printf("%d ",segment.qkth(l,r,k)); } if(opt==3){ segment.change(1,1,n,l,l,r); val[l]=r; } if(opt==4){ int k=read(); printf("%d ",segment.qpre(1,1,n,l,r,k)); } if(opt==5){ int k=read(); printf("%d ",segment.qnex(1,1,n,l,r,k)); } } return 0; }
