Description
在一个 (n imes n) 的二维平面上,支持两种操作,操作共 (q) 组:
- 加入一个 权值为 (v) 的二维点 ((x,y))。
- 在所有满足 (x_1 le xle x_2 ext{ and } y_1le yle y_2) 的点中,找出点权第 (k) 大的点,输出它的点权。或者判断是否存在。
强制在线。
Hint
(1le nle 5 imes 10^5,1le qle 10^5)
(1le vle 10^9,1le kle q)
Solution
题目有一个操作是求 ( ext{k-th}),那么很容易想到权值线段树,而且实现十分简单。
下面是(动态开点)权值线段树 的 查找 ( ext{k-th}) 的代码:
int sgtQueryKth(int k,int l=1,int r=INT_MAX,int rt=sgtRt) {
if(!rt) return -1;
if(l==r) return l;
int mid=(l+r)>>1;
if(size[rc[rt]]>=k)
return sgtQueryKth(k,mid+1,r,rc[rt]);
else
return sgtQueryKth(k-size[rc[rt]],l,mid,lc[rt]);
}
其中,size[rc[rt]] 是 全局 中 结点 rc[rt] 所管辖值域中的 元素的个数。
然而现在我们有了限制,怎么办?我们需要快速计算 限定矩形范围 中 结点 rc[rt] 所管辖值域中的 元素的个数。
那么不难想到用 KD-Tree 来维护,实际上就是二维数点。再具体一点,就是 权值线段树的每个结点 都维护一个 KD-Tree,对于权值线段树上的结点 rt 那么 rt 上的 KDT 就维护着 结点 rt 所管辖的值域中的所有二维点。
所有,只需要再原来朴素的权值线段树的代码上,改一下……
int sgtQueryKth(int xL,int xR,int yL,int yR,int k,int l=1,int r=V,int rt=sgtRt) {
if(l==r) return l;
int insideCnt=kdtCount(xL,xR,yL,yR,kdtRt[rc[rt]]); // 在当前结点的右儿子的 KDT 上做二维数点。
if(insideCnt>=k)//之后的所有原来的 size[rc[rt]] 都换为 insideCnt
return sgtQueryKth(xL,xR,yL,yR,k,mid+1,r,rc[rt]);
else
return sgtQueryKth(xL,xR,yL,yR,k-insideCnt,l,mid,lc[rt]);
}
emm……基本没变??
是的。
那么插入的操作也可以很快写出来了:
void sgtUpdate(int *dat,int v,int l=1,int r=V,int &rt=sgtRt) {//dat[0] => x坐标,dat[1] => y坐标
if(!rt) rt=++sgtNCnt;
kdtInsert(dat,kdtRt[rt]);//原本为 size[rt]+=v ,现换成 KDT 的插入
if(l==r) return;
if(v<=mid) sgtUpdate(dat,v,l,mid,lc[rt]);
else sgtUpdate(dat,v,mid+1,r,rc[rt]);
//不要直接 pushup,随便想想就知道那样子复杂度会爆炸,应使用 Path-update 的方式。
}
那么,这就是传说中的树套树中的 权值线段树 套 KD-Tree 了!
【镇楼】
权值线段树 套 KDT 的图示:
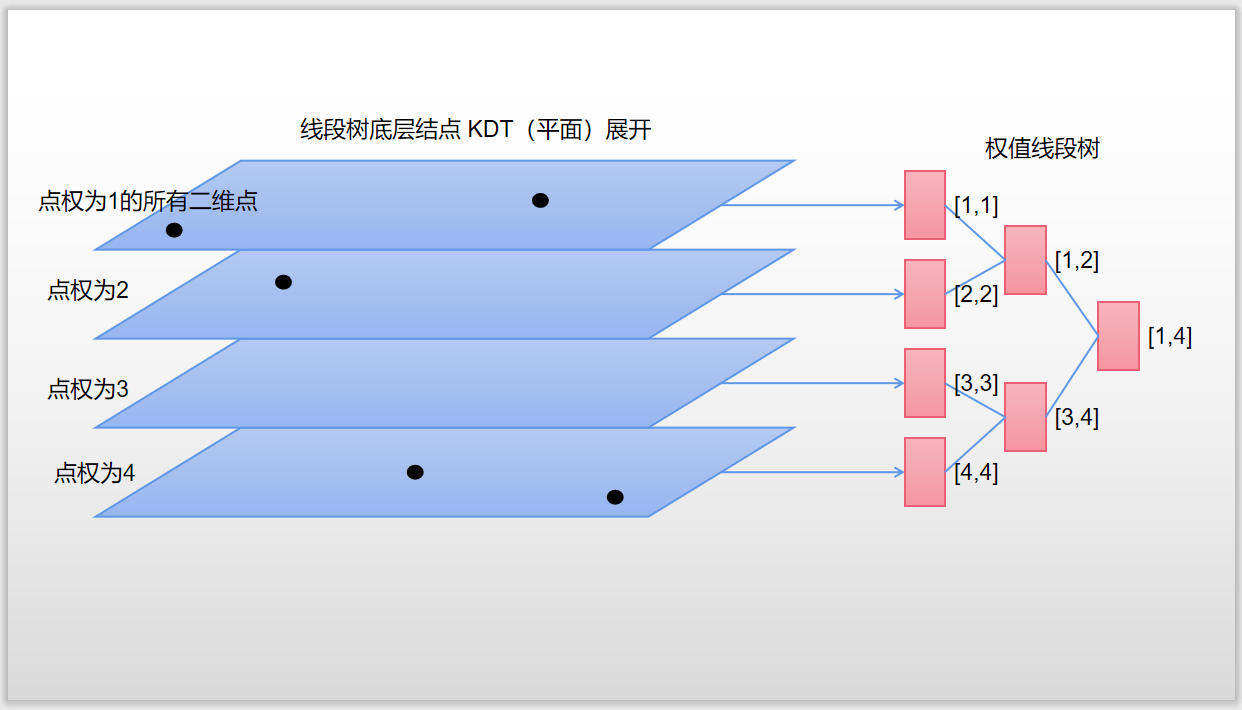
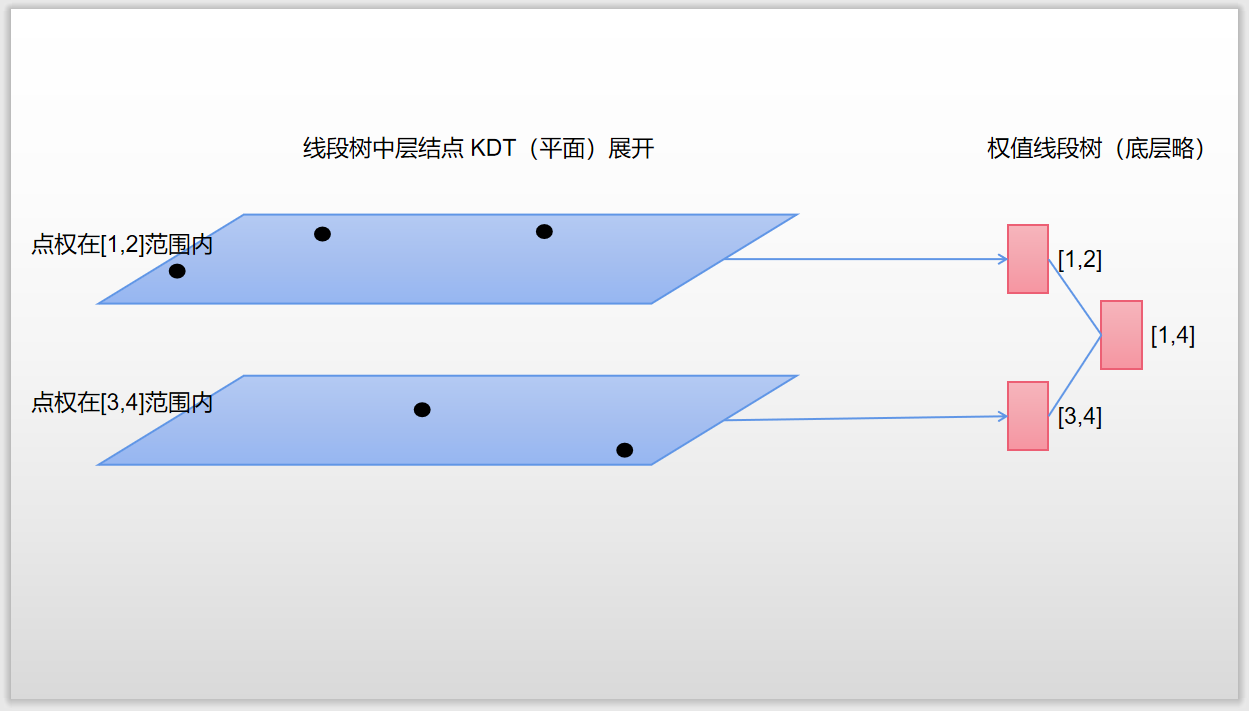
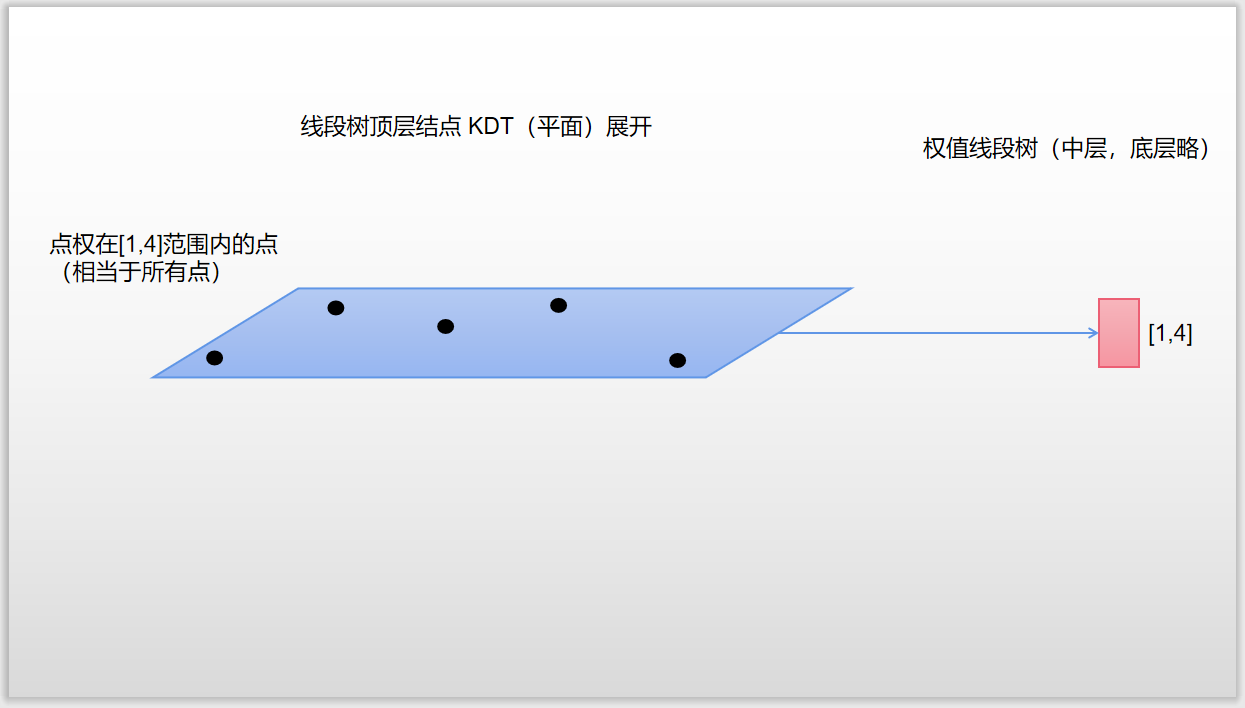
Code
完整代码(O2)
/*
* Author : _Wallace_
* Source : https://www.cnblogs.com/-Wallace-/
* Problem : LOJ #6016 崂山白花蛇草水
*/
#include<cstdio>
#include<algorithm>
#include<utility>
using namespace std;
namespace fastIO_int {
int get_int() {
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9') {
if(c=='-')f=-1;
c=getchar();
}
while(c>='0'&&c<='9')
x=x*10+c-'0',c=getchar();
return f*x;
}
void read(){}
template<class T1,class ...T2>
void read(T1 &i,T2&... rest) {
i=get_int();
read(rest...);
}
void put_int(int x) {
if(x<0)putchar('-'),x=-x;
if(x>9)put_int(x/10);
putchar(x%10+'0');
}
void write(){}
template<class T1,class ...T2>
void write(T1 i,T2... rest) {
put_int(i),putchar(' ');
write(rest...);
}
};
const int V=1e9;
const int N=1e5+5;
#define lc(x) tree[x].lc
#define rc(x) tree[x].rc
struct Node {
int lc,rc,size;
int dat[2];
int Max[2],Min[2];
Node() {
lc=rc=size=0;
dat[0]=dat[1]=0;
Max[0]=Max[1]=Min[0]=Min[1]=0;
}
Node(int x,int y) {
lc=rc=0,size=1;
dat[0]=x,dat[1]=y;
Max[0]=Min[0]=x,Max[1]=Min[1]=y;
}
inline int& operator [] (const int &t) {
return dat[t];
}
}tree[N<<6];
int kdtNCnt;
inline void maintain(int rt) {
for(register int i=0;i<2;i++) {
tree[rt].Max[i]=tree[rt].Min[i]=tree[rt][i];
if(lc(rt)) {
tree[rt].Max[i]=max(tree[rt].Max[i],tree[lc(rt)].Max[i]);
tree[rt].Min[i]=min(tree[rt].Min[i],tree[lc(rt)].Min[i]);
}
if(rc(rt)) {
tree[rt].Max[i]=max(tree[rt].Max[i],tree[rc(rt)].Max[i]);
tree[rt].Min[i]=min(tree[rt].Min[i],tree[rc(rt)].Min[i]);
}
}
tree[rt].size=tree[lc(rt)].size+tree[rc(rt)].size+1;
}
namespace kdtRebuildPart {
#define alpha 0.75
pair<int,int> pnt[N];
int stk[N],top=0;
struct comparator {
int dim;
inline bool operator () (const pair<int,int> &x,const pair<int,int> &y) const {
if(dim==0) return x.first < y.first;
else return x.second < y.second;
}
}cmp;
int build(int l,int r,int d) {
if(l>r) return 0;
int rt=stk[top--], mid=(l+r)>>1;
cmp.dim=d;
nth_element(pnt+l,pnt+mid,pnt+r+1,cmp);
tree[rt]=Node(pnt[mid].first,pnt[mid].second);
lc(rt)=build(l,mid-1,d^1);
rc(rt)=build(mid+1,r,d^1);
return maintain(rt),rt;
}
void destroy(int rt) {
if(!rt) return;
stk[++top]=rt;
pnt[top]=make_pair(tree[rt][0],tree[rt][1]);
destroy(lc(rt));
destroy(rc(rt));
}
inline bool isBalanced(int rt) {
if(tree[rt].size*alpha<tree[lc(rt)].size*1.0) return false;
if(tree[rt].size*alpha<tree[rc(rt)].size*1.0) return false;
return true;
}
inline void rebuild(int &rt,int d) {
if(isBalanced(rt)) return;
top=0,destroy(rt);
rt=build(1,top,d);
}
#undef alpha
}
void kdtInsert(int *dat,int &rt,int d=0) {
if(!rt) {
rt=++kdtNCnt;
tree[rt]=Node(dat[0],dat[1]);
return;
}
if(dat[d]<=tree[rt][d])
kdtInsert(dat,lc(rt),d^1);
else
kdtInsert(dat,rc(rt),d^1);
maintain(rt);
kdtRebuildPart::rebuild(rt,d);
}
inline bool allIn(int xL,int xR,int yL,int yR,int rt) {
return (tree[rt].Max[0]<=xR&&tree[rt].Max[1]<=yR&&tree[rt].Min[0]>=xL&&tree[rt].Min[1]>=yL);
}
inline bool allOut(int xL,int xR,int yL,int yR,int rt) {
return (tree[rt].Max[0]<xL||tree[rt].Max[1]<yL||tree[rt].Min[0]>xR||tree[rt].Min[1]>yR);
}
inline int checkIn(int xL,int xR,int yL,int yR,int rt) {
return !(tree[rt][0]<xL||tree[rt][0]>xR||tree[rt][1]<yL||tree[rt][1]>yR);
}
int kdtCount(int xL,int xR,int yL,int yR,int rt) {
if(!rt) return 0;
if(allIn(xL,xR,yL,yR,rt)) return tree[rt].size;
if(allOut(xL,xR,yL,yR,rt)) return 0;
int ret=checkIn(xL,xR,yL,yR,rt);
return ret+kdtCount(xL,xR,yL,yR,lc(rt))+kdtCount(xL,xR,yL,yR,rc(rt));
}
#undef lc
#undef rc
#define mid ((l+r)>>1)
int kdtRt[N<<4];
int lc[N<<4],rc[N<<4];
int sgtNCnt=0;
int sgtRt=0;
void sgtUpdate(int *dat,int v,int l=1,int r=V,int &rt=sgtRt) {
if(!rt) rt=++sgtNCnt;
kdtInsert(dat,kdtRt[rt]);
if(l==r) return;
if(v<=mid) sgtUpdate(dat,v,l,mid,lc[rt]);
else sgtUpdate(dat,v,mid+1,r,rc[rt]);
}
int sgtQueryKth(int xL,int xR,int yL,int yR,int k,int l=1,int r=V,int &rt=sgtRt) {
if(l==r) return l;
int insideCnt=kdtCount(xL,xR,yL,yR,kdtRt[rc[rt]]);
if(insideCnt>=k)
return sgtQueryKth(xL,xR,yL,yR,k,mid+1,r,rc[rt]);
else
return sgtQueryKth(xL,xR,yL,yR,k-insideCnt,l,mid,lc[rt]);
}
#undef mid
int n,q;
signed main() {
using fastIO_int::read;
using fastIO_int::write;
read(n,q);
for(int last=0;q;--q) {
int cmd; read(cmd);
if(cmd==1) {
int dat[2],v;
read(dat[0],dat[1],v);
dat[0]^=last;
dat[1]^=last;
v^=last;
sgtUpdate(dat,v);
} else {
int xL,yL,xR,yR,k;
read(xL,yL,xR,yR,k);
xL^=last,xR^=last;
yL^=last,yR^=last;
k^=last;
if(kdtCount(xL,xR,yL,yR,kdtRt[sgtRt])<k) {
last=0;
puts("NAIVE!ORZzyz.");
} else {
last=sgtQueryKth(xL,xR,yL,yR,k);
write(last),putchar('
');
}
}
}
return 0;
}