NOIP模拟赛
by thmyl
|
题目名称 |
superman |
market |
Lemon_Soda |
|
可执行文件名 |
superman |
market |
Lemon_Soda |
|
输入文件 |
superman.in |
market.in |
Lemon_Soda.in |
|
输出文件 |
superman.out |
market.out |
Lemon_Soda.out |
|
时间限制 |
1s |
1s |
1s |
|
是否有部分分 |
无 |
无 |
无 |
|
满分 |
100 |
100 |
100 |
|
空间限制 |
250M |
128M |
128M |
|
测试点数量 |
5 |
10 |
10
|
Problem 1. superman
【题目描述】
小可乐是要登上世界顶峰的男人!为了向他的妹子证明自己的能力,他决定去撒哈拉沙漠找到依米花送给他的妹子。
假设途中经过N个地区,编号为1~N,小可乐一开始在编号为1的地区,编号为N的地区代表撒哈拉沙漠,地区之间由于地形差别悬殊,并不是都可以直连的。同时由于不同经度存在时差,小可乐看了当地的地方时会以为出现了时间静止甚至倒流,所以我们假设两地区之间的穿行时间可以是负数或0,另外,由地区i到地区j的时间和由地区j到地区i的时间不一定是相同的。
小可乐在非洲的网友DDL被他感动了,决定去城市n迎接小可乐的到来,小可乐可以自己调整行动速度,为了不让DDL等得太着急,他想调整自己行动的速度,使得在每一条路上花费的时间都加或减一个整数,你的任务是调整小可乐的行动速度,找出一条用最短时间到达地区N的路径,并且保证这个最短时间的值大于或等于0。
【输入格式】
输入文件包含多组数据,第1个数为T,表示数据的数量。
对于每一组数据,输入第1行为两个正整数N,E,为地区的个数和地区间的路线数。然后E行,每行三个整数i,j和t(1≤i,j≤N,i≠j),表示由地区i到地区j穿行的时间为t。由i到j最多只会有一条穿行线路。
【输出格式】
输出文件共T行,每组数据输出一行;
如果可以通过调节速度到达地区N,则输出一个非负整数,表示由地区1到地区N的最短时间。
如果不能由地区1到达地区N,则输出-1。
【输入样例】
1
4 5
1 2 1
1 3 1
2 3 -3
3 1 1
3 4 1
【输出样例】
2
【样例说明】
输入样例如图所示,其中节点标号表示相应地区,节点间数字表示所需时间。
如果设置控制速度的值为0,则有如下路径:1→2→3→1→2→……→3→4,使得投递的时间为负无穷大,显然是不符合要求的,所以应该把控制速度的值设为1,相当于每个时间值加1,得到的最短路径为1→2→3→4,所需时间为2+(-2)+2=2。
题目大意:给每条边加上或减去一个数,使得最短路没有负环,且最短路为非负整数解。
题解:floyed判断连通性+spfa求最短路。
代码:
#include<iostream> #include<cstdio> #include<queue> #include<cstring> #define maxn 100005 using namespace std; int n,e,t,l=0x7ffffff,r=-0x7ffffff,sumedge,ans; int head[maxn],dis[maxn],vis[maxn],inq[maxn]; struct Edge{ int x,y,z,nxt; Edge(int x=0,int y=0,int z=0,int nxt=0): x(x),y(y),z(z),nxt(nxt){} }edge[maxn<<1]; void add(int x,int y,int z){ edge[++sumedge]=Edge(x,y,z,head[x]); head[x]=sumedge; } void updata(){ memset(dis,0,sizeof(dis)); memset(head,0,sizeof(dis)); memset(inq,0,sizeof(inq)); memset(vis,0,sizeof(vis)); sumedge=0; } bool spfa(int s){ queue<int>q; memset(vis,0,sizeof(vis)); memset(inq,0,sizeof(inq)); memset(dis,0x3f,sizeof(dis)); while(!q.empty())q.pop(); dis[1]=0;inq[1]=1;q.push(1);vis[1]=1; while(!q.empty()){ int now=q.front();q.pop(); inq[now]=0; for(int i=head[now];i;i=edge[i].nxt){ int v=edge[i].y; if(dis[v]>dis[now]+edge[i].z+s){ dis[v]=dis[now]+edge[i].z+s; if(!inq[v]){ inq[v]=1; q.push(v); vis[v]++; if(vis[v]>n)return 0; } } } } if(dis[n]<0)return 0; return 1; } int main(){ scanf("%d",&t); while(t--){ scanf("%d%d",&n,&e); updata(); for(int i=1;i<=e;i++){ int x,y,z; scanf("%d%d%d",&x,&y,&z); add(x,y,z); l=min(l,z); r=max(r,z); } while(l<=r){ int mid=(l+r)>>1; if(spfa(mid)){ ans=dis[n]; r=mid-1; }else l=mid+1; } if(ans==0x3f3f3f3f){ printf("-1 "); }else printf("%d ",ans); } return 0; }
没测 没测的代码一般都0蛋
Problem 2. market
【题目描述】
小可乐的妹子不在家,他只好自己去逛超市,小可乐最喜欢喝汽水,买到汽水会使小可乐开心起来,但是他也不愿意看到手里的毛毛变少,所以每买一瓶汽水也会有点难过,很显然他又遇到了很多麻烦。
现在小可乐面前有n瓶汽水,编号分别为1,2,3,……,n。他可以在这当中任意选择任意多瓶。其中第i瓶汽水有两个属性Wi和Ri,当他选择了第i瓶汽水后,就可以获得Wi的开心值;但是,他选择该汽水以后选择的所有汽水的开心值都会减少Ri。现在请你求出,该选择哪些汽水,并且该以什么样的顺序选取这些汽水,才能使得小可乐获得的开心值最大。
注意,开心值的减少是会叠加的。比如,选择了第i瓶汽水,那么就会获得Wi的开心值;然后又选择第j瓶汽水,又会获得了Wj-Ri开心值;之后又选择第k瓶汽水,又会获得Wk-Ri-Rj的开心值;那么他获得的开心值总和为Wi+(Wj-Ri)+(Wk-Ri-Rj)。
【输入格式】
第一行一个正整数n,表示汽水的瓶数。
接下来第2行到第n+1行,每行两个正整数Wi和Ri,含义如题目所述。
【输出格式】
输出仅一行,表示最大的开心值。
【输入样例】
2
5 2
3 5
【输出样例】
6
【说明】
20%的数据满足:n<=5,0<=Wi,Ri<=1000。
50%的数据满足:n<=15,0<=Wi,Ri<=1000。
100%的数据满足:n<=3000,0<=Wi,Ri<=200000。
样例解释:我们可以选择第1瓶汽水,获得了5点开心值;之后我们再选择第2瓶汽水,获得3-2=1点开心值。最后总的开心值为5+1=6。
题解:
贪心+dp
dfs10分 忘记全排列。
我们可知 如果固定选k个物品的话,一定不能先选r大的。如果先选,这个r将减少多个物品的价值。
首先将r从大到小排序,如果选择这个物品,那么这个物品使它被选之前的所有物品价值-r。
转移方程很好想,选这个物品和不选这个物品两个状态中选取一个最大的。
代码:
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; int n,ans,f[3020][3020]; struct E{ int w,r; bool operator < (const E &a)const{return r>a.r;} }s[3010]; int main(){ scanf("%d",&n); for(int i=1;i<=n;i++)scanf("%d%d",&s[i].w,&s[i].r); sort(s+1,s+n+1); for(int i=1;i<=n;i++) for(int j=1;j<=i;j++) f[i][j]=max(f[i-1][j],f[i-1][j-1]+s[i].w-s[i].r*(j-1)); for(int i=1;i<=n;i++)ans=max(ans,f[n][i]); cout<<ans<<endl; return 0; }
Problem 3. Lemon_Soda
【题目描述】
小可乐惊喜的发现一瓶汽水中了再来一瓶,他去商店换汽水的时候,店主Lemon和Soda打算耍耍他,出了一个难题,而且做不出来就不给汽水喝
这题说的是:
使得 达到或超过 n 位数字的最小正整数 x 是多少?
小可乐见了两位妹子紧张的不敢说话,快请你帮帮他解决这个难题吧
【输入格式】
一个正整数 n
【输出格式】
使得 达到 n 位数字的最小正整数 x
【输入样例】
11
【输出样例】
10
【说明】
n<=2000000000
换底公式
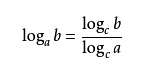
题解:二分答案
实质是求
x^x>=10^(n-1),
log(x^x)>=log(10^(n-1))
x*log(x)>=n-1
因为左边是单调的 二分即可。
代码
#include<iostream> #include<cstdio> #include<cmath> using namespace std; int l,r,ans,n; bool check(int x){ if(x*log(x)/log(10)>=n-1)return 1; return 0; } int main(){ scanf("%d",&n); l=0;r=2000000000; while(l<=r){ int mid=(l+r)>>1; if(check(mid)){ ans=mid; r=mid-1; } else l=mid+1; } cout<<ans<<endl; return 0; }