影响排序性能的要素:
时间性能;
辅助空间
算法的复杂度
简单排序【n^2】
算法思想:
第一趟:
从第一个记录开始,通过n-1次关键字比较,从n个记录中选出最小的并和第一个记录交换;
第二趟:
从第二个记录开始,通过n-2次关键字比较,从n -1个记录中选出最小的并和第二个记录交换;
复杂度稳稳的是0(n2),几乎被抛弃
1 void SimpleSort() 2 { 3 for (int i = 0; i < n; ++i) 4 { 5 int minV = v[i], index = i; 6 for (int j = i + 1; j < n; ++j) 7 { 8 if (minV > v[j]) 9 { 10 minV = v[j]; 11 index = j; 12 } 13 } 14 swap(v[i], v[index]); 15 } 16 }
冒泡排序
冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。
它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果他们的顺序(如从大到小、首字母从A到Z)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素列已经排序完成。
这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),故名“冒泡排序”。每一次排序都将最大的数排到最后【最前】
算法稳定性:
冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较,交换也发生在这两个元素之间。所以,如果两个元素相等,是不会再交换的;如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法。
1 void bubble_sort(T arr[], int len) 2 { 3 int i, j; T temp; 4 for (i = 0; i < len; i++) 5 for (j = 0; j < len - i - 1; j++)//之所以是-i,是因为每一次j的循环都将最大的数冒出到最后,所以后面的i个数是已经完成了排序的 6 if (arr[j] > arr[j + 1]) 7 { 8 temp = arr[j]; 9 arr[j] = arr[j + 1]; 10 arr[j + 1] = temp; 11 } 12 }
改进:
使用一个标记,一旦某次j循环遍历中没有进行数据交换,那么数据是提前有序了,使用flag进行标记提前结束循环。
选择排序
选择排序(Selection sort)是一种简单直观的排序算法。
它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。【好像就是前面的简单排序】
稳定性:
选择排序是给每个位置选择当前元素最小的,比如给第一个位置选择最小的,在剩余元素里面给第二个元素选择第二小的,依次类推,直到第n-1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。那么,在一趟选择,如果一个元素比当前元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。比较拗口,举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中两个5的相对前后顺序就被破坏了,所以选择排序是一个不稳定的排序算法。
1 void SelectSort() 2 { 3 for (int i = 0; i < n; ++i) 4 { 5 int index = i; 6 for (int j = i + 1; j < n; ++j) 7 if (v[index] > v[j]) 8 index = j; 9 if (index != i) 10 { 11 int temp = v[i]; 12 v[i] = v[index]; 13 v[index] = temp; 14 } 15 } 16 }
插入排序
插入排序(Insertion sort)是一种简单直观且稳定的排序算法。如果有一个已经有序的数据序列,要求在这个已经排好的数据序列中插入一个数,但要求插入后此数据序列仍然有序,这个时候就要用到一种新的排序方法——插入排序法,插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据,算法适用于少量数据的排序,时间复杂度为O(n^2)。是稳定的排序方法。
插入算法把要排序的数组分成两部分:第一部分包含了这个数组的所有元素,但将最后一个元素除外(让数组多一个空间才有插入的位置),而第二部分就只包含这一个元素(即待插入元素)。在第一部分排序完成后,再将这个最后元素插入到已排好序的第一部分中。
插入排序的基本思想是:
一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下:
·从第一个元素开始,该元素可以认为已经被排序;
·取出下一个元素,在已经排序的元素序列中从后向前扫描;
·如果该元素(已排序)大于新元素,将该元素移到下一位置;
·重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
·将新元素插入到该位置后;
直接插入排序:
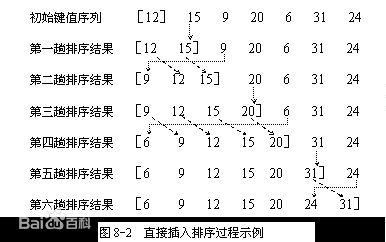
直接插入排序是一种简单的插入排序法,其基本思想是:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列。
直接插入排序的算法思路:
(1) 设置监视哨temp,将待插入记录的值赋值给temp;
(2) 设置开始查找的位置j = i-1,从判断比较的i位置的前一个数开始比较;
(3) 在数组中进行搜索,搜索中将第j个记录后移,直至temp≥r[j].key为止;
(4) 将temp插入r[j+1]的位置上。
直接插入排序算法:
1 void InsertSort() 2 { 3 int temp;//临时哨兵 4 for (int i = 1; i < n; ++i) 5 { 6 temp = v[i]; 7 int j = i - 1; 8 for (; j >= 0; --j)//从i的前一位开始从后向前比较 9 if (temp < v[j]) 10 v[j + 1] = v[j];//向后移 11 else 12 break;//找到位置了 13 v[j+1] = temp;//注意,j前移动了 14 } 15 }
算法的基本过程:折半插入排序(二分插入排序)
(1)计算 0 ~ i-1 的中间点,用 i 索引处的元素与中间值进行比较,如果 i 索引处的元素大,说明要插入的这个元素应该在中间值和刚加入i索引之间,反之,就是在刚开始的位置到中间值的位置,这样很简单的完成了折半;
(2)在相应的半个范围里面找插入的位置时,不断的用(1)步骤缩小范围,不停的折半,范围依次缩小为 1/2 1/4 1/8 .......快速的确定出第 i 个元素要插在什么地方;
(3)确定位置之后,将整个序列后移,并将元素插入到相应位置。
1 #include<iterator> 2 template<typename biIter> 3 void insertion_sort (biIter begin, biIter end) 4 { 5 typedef typename std::iterator_traits<biIter>::value_type value_type; 6 biIter bond = begin; 7 std::advance(bond, 1); 8 for (; bond != end; std::advance(bond, 1)) 9 { 10 value_type key = *bond; 11 biIter ins = bond; 12 biIter pre = ins; 13 std::advance(pre, -1); 14 while (ins != begin && *pre > key) 15 { 16 *ins = *pre; 17 std::advance(ins, -1); 18 std::advance(pre, -1); 19 } 20 *ins = key; 21 } 22 }
希尔排序
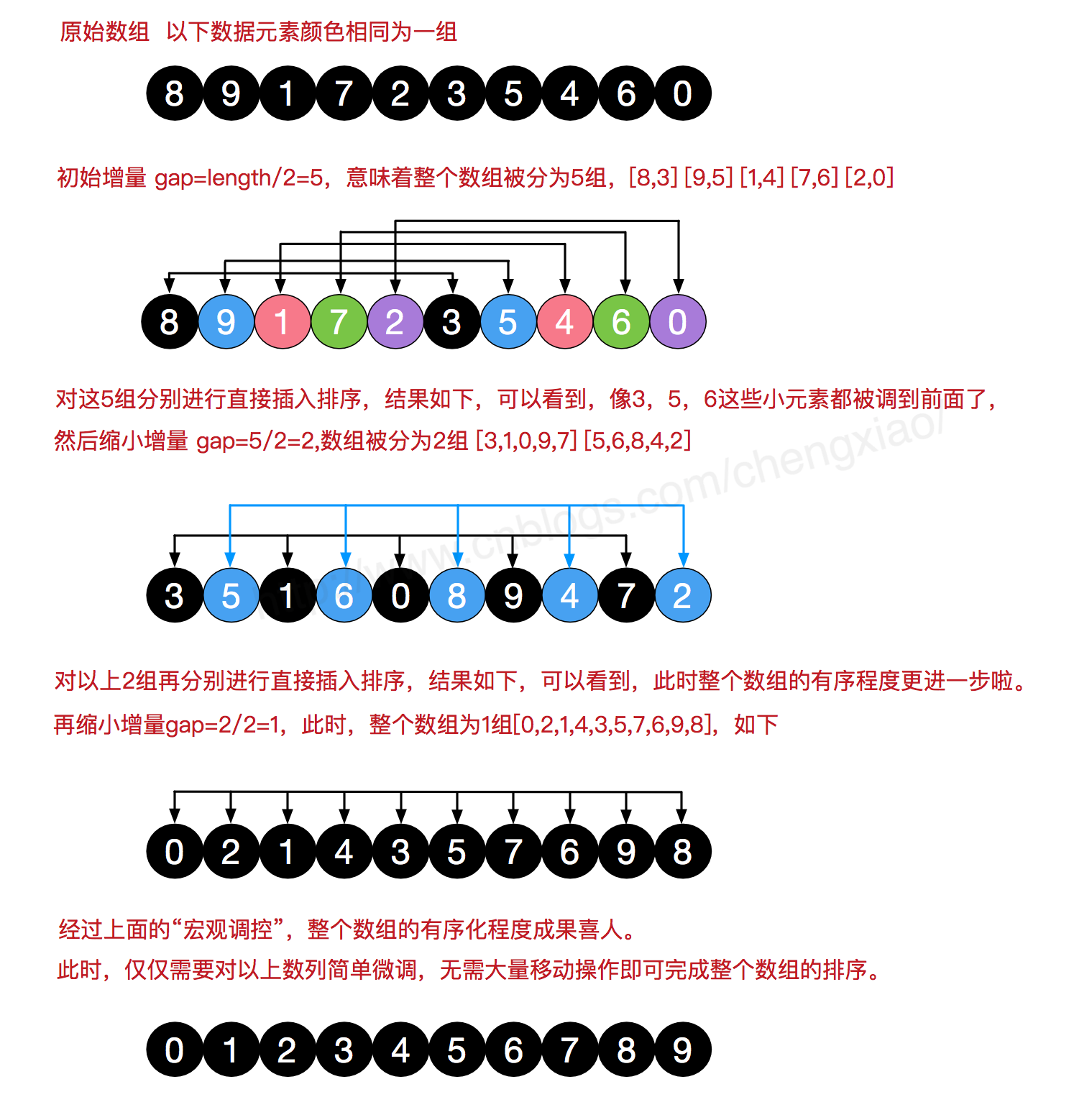
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell于1959年提出而得名。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
先取一个小于n的整数d1作为第一个增量,把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序;
然后,取第二个增量d2<d1重复上述的分组和排序,直至所取的增量 =1( < …<d2<d1),即所有记录放在同一组中进行直接插入排序为止。该方法实质上是一种分组插入方法
一般的初次取序列的一半为增量,以后每次减半,直到增量为1。
稳定性:
由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以shell排序是不稳定的。
1 void ShellSort() 2 { 3 for (int gap = n / 2; gap > 0; gap /= 2)//gap为组的跨度,初始取长度的一半,此后每一次都折半取 4 { 5 //对于每个跨度为gap的数据进行插入排序 6 for (int i = 0; i < gap; ++i)//每次i与跨度为gap的j一起比较 7 { 8 for (int j = i + gap; j < n; j+=gap)//j对应的是i的跨度为gap的数值 9 { 10 if (v[j] < v[j - gap])//后比前小,应该向前插入 11 { 12 int k = j - gap, temp = v[j];//temp哨兵 13 while (k >= 0 && v[k] > temp) 14 { 15 v[k + gap] = v[k];//后移 16 k -= gap; 17 } 18 19 v[k + gap] = temp;//k-gap了,故需加上gap 20 } 21 } 22 } 23 } 24 }
归并排序
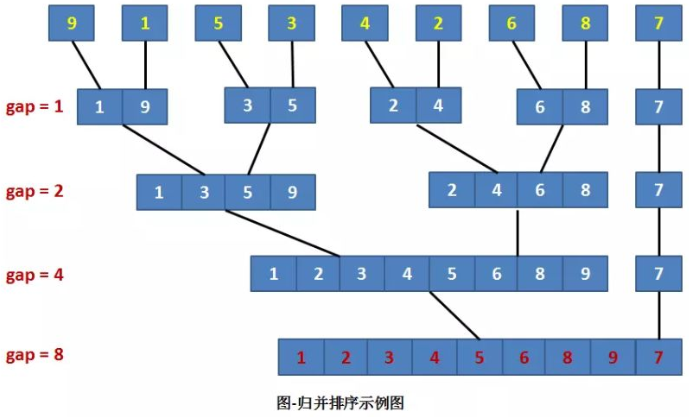
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并操作(merge),也叫归并算法,指的是将两个顺序序列合并成一个顺序序列的方法。
算法稳定性:
在归并排序中,相等的元素的顺序不会改变,所以它是稳定的算法。
归并操作的工作原理如下:[数组1小,数组1的数字上,否则数组2的数上]
第一步:申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
第二步:设定两个指针,最初位置分别为两个已经排序序列的起始位置
第三步:比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
重复步骤3直到某一指针超出序列尾,将另一序列剩下的所有元素直接复制到合并序列尾
两个数组进行归并:
1 //两个数组进行归并 2 void Merge(int iL, int iR, int jL, int jR)//此处的L,R分别为两个小数组的边界 3 { 4 vector<int>temp(jR - iL + 1);//开辟大小为两个数组的大小空间 5 int k = 0, i = iL, j = jL; 6 while (i <= iR && j <= jR) 7 { 8 if (v[i] <= v[j])//此处的等号保证了算法的稳定性,使得相同数值前后位置不变 9 temp[k++] = v[i++]; 10 else 11 temp[k++] = v[j++]; 12 } 13 while (i <= iR)//数组1未完 14 temp[k++] = v[i++]; 15 while (j <= jR)//数组2未完 16 temp[k++] = v[j++]; 17 18 for (i = iL, k = 0; i <= jR; ++k, ++i) 19 20 v[i] = temp[k]; 21 22 } 23 24
自底向上:非递归版【小数组到大数组】 :
1 void MergeSort() 2 { 3 //step为小数组的大小,此处step的代表为两个小数组的大小,故定是2的倍数 4 for (int step = 2; step / 2 < n; step *= 2)//1&1组,2&2组,4&4组。。。。 5 {//一定是从1与1的数组开始!!!不然就没法保证排序了 6 for (int i = 0; i < n; i += step) 7 //sort(v + i, v + min(i + step, n));//直接使用自带的sort函数进行排序 8 if ((i + step / 2 ) < n)//中间节点 9 Merge(i, i + step / 2 - 1, i + step / 2, min(i + step - 1, n - 1));//从i开始,在跨度为step中分为两个小数组进行归并 10 } 11 }
自顶向下:递归版【大数组到小数组】 :
1 void MergeSort(int L, int R) 2 { 3 if (L < R)//一定不能等于 4 { 5 int mid = L + (R - L) / 2;//求中点 6 MergeSort(L, mid);//对左边进行递归切分成小数组 7 MergeSort(mid + 1, R);//对右边进行递归切分成小数组 8 Merge(L, mid, mid + 1, R);//将左右两边进行归并 9 } 10 }
快速排序:
快速排序(Quicksort)是对冒泡排序的一种改进。快速排序由C. A. R. Hoare在1960年提出。 快速排序
它的基本思想是:
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
设要排序的数组是A[0]……A[N-1],首先任意选取一个数据(通常选用数组的第一个数)作为关键数据,然后将所有比它小的数都放到它左边,所有比它大的数都放到它右边,这个过程称为一趟快速排序。值得注意的是,快速排序不是一种稳定的排序算法,也就是说,多个相同的值的相对位置也许会在算法结束时产生变动。
一趟快速排序的算法是:
1)设置两个变量i、j,排序开始的时候:i=0,j=N-1;
2)以第一个数组元素作为关键数据,赋值给key,即key=A[0];
3)从j开始向前搜索,即由后开始向前搜索(j--),直到找到第一个小于key的值A[j],将A[j]和A[i]的值交换;
4)从i开始向后搜索,即由前开始向后搜索(i++),直到找到第一个大于key的A[i],将A[i]和A[j]的值交换;
5)重复第3、4步,直到i==j; (3,4步中,没找到符合条件的值,即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值,使得j=j-1,i=i+1,直至找到为止。找到符合条件的值,进行交换的时候i, j指针位置不变。另外,i==j这一过程一定正好是i+或j-完成的时候,此时令循环结束)

1 //对区间进行划分 2 int Partition(int L, int R) 3 { 4 //int p = round(1.0*rand() / RAND_MAX * (R - L) + L);//选取随机位置的数为基准值 5 //swap(v[L], v[p]);//将基准值换到最左边 6 int key = v[L];//一般默认使用最左端的值为基准值 7 while (L < R) 8 { 9 while (L < R && v[R]>key)--R;//从右向左,直到找到比key小的数 10 v[L] = v[R];//将小的数移到左边 11 while (L < R && v[L] <= key)++L;//从左向右,直到找到比key大数 12 v[R] = v[L];//将大的数移到右边 13 } 14 v[L] = key;//key在中间的位置 15 return L;//返回中点坐标 16 } 17 18 void QuickSort(int L, int R) 19 { 20 if (L < R) 21 { 22 int pos = Partition(L, R); 23 QuickSort(L, pos - 1);//对左子区间进行快速排序 24 QuickSort(pos + 1, R);//对右子区间进行快速排序 25 } 26 }
三平均分区法
关于这一改进的最简单的描述大概是这样的:与一般的快速排序方法不同,它并不是选择待排数组的第一个数作为中轴,而是选用待排数组最左边、最右边和最中间的三个元素的中间值作为中轴。这一改进对于原来的快速排序算法来说,主要有两点优势:
(1) 首先,它使得最坏情况发生的几率减小了。
(2) 其次,未改进的快速排序算法为了防止比较时数组越界,在最后要设置一个哨点。
根据分区大小调整算法
这一方面的改进是针对快速排序算法的弱点进行的。快速排序对于小规模的数据集性能不是很好。可能有人认为可以忽略这个缺点不计,因为大多数排序都只要考虑大规模的适应性就行了。但是快速排序算法使用了分治技术,最终来说大的数据集都要分为小的数据集来进行处理。由此可以得到的改进就是,当数据集较小时,不必继续递归调用快速排序算法,而改为调用其他的对于小规模数据集处理能力较强的排序算法来完成。
不同的分区方案考虑
对于快速排序算法来说,实际上大量的时间都消耗在了分区上面,因此一个好的分区实现是非常重要的。尤其是当要分区的所有的元素值都相等时,一般的快速排序算法就陷入了最坏的一种情况,也即反复的交换相同的元素并返回最差的中轴值。无论是任何数据集,只要它们中包含了很多相同的元素的话,这都是一个严重的问题,因为许多“底层”的分区都会变得完全一样。
对于这种情况的一种改进办法就是将分区分为三块而不是原来的两块:一块是小于中轴值的所有元素,一块是等于中轴值的所有元素,另一块是大于中轴值的所有元素。
另一种简单的改进方法是,当分区完成后,如果发现最左和最右两个元素值相等的话就避免递归调用而
采用其他的排序算法来完成。
并行的快速排序
由于快速排序算法是采用分治技术来进行实现的,这就使得它很容易能够在多台处理机上并行处理。
在大多数情况下,创建一个线程所需要的时间要远远大于两个元素比较和交换的时间,因此,快速排序的并行算法不可能为每个分区都创建一个新的线程。一般来说,会在实现代码中设定一个阀值,如果分区的元素数目多于该阀值的话,就创建一个新的线程来处理这个分区的排序,否则的话就进行递归调用来排序。
随机化快排
快速排序的最坏情况基于每次划分对主元的选择。基本的快速排序选取第一个元素作为主元。这样在数组已经有序的情况下,每次划分将得到最坏的结果。一种比较常见的优化方法是随机化算法,即随机选取一个元素作为主元。这种情况下虽然最坏情况仍然是O(n^2),但最坏情况不再依赖于输入数据,而是由于随机函数取值不佳。实际上,随机化快速排序得到理论最坏情况的可能性仅为1/(2^n)。所以随机化快速排序可以对于绝大多数输入数据达到O(nlogn)的期望时间复杂度。一位前辈做出了一个精辟的总结:“随机化快速排序可以满足一个人一辈子的人品需求。”
随机化快速排序的唯一缺点在于,一旦输入数据中有很多的相同数据,随机化的效果将直接减弱。对于极限情况,即对于n个相同的数排序,随机化快速排序的时间复杂度将毫无疑问的降低到O(n^2)。解决方法是用一种方法进行扫描,使没有交换的情况下主元保留在原位置。
平衡快排
每次尽可能地选择一个能够代表中值的元素作为关键数据,然后遵循普通快排的原则进行比较、替换和递归。通常来说,选择这个数据的方法是取开头、结尾、中间3个数据,通过比较选出其中的中值。取这3个值的好处是在实际问题中,出现近似顺序数据或逆序数据的概率较大,此时中间数据必然成为中值,而也是事实上的近似中值。万一遇到正好中间大两边小(或反之)的数据,取的值都接近最值,那么由于至少能将两部分分开,实际效率也会有2倍左右的增加,而且利于将数据略微打乱,破坏退化的结构。
外部快排
与普通快排不同的是,关键数据是一段buffer,首先将之前和之后的M/2个元素读入buffer并对该buffer中的这些元素进行排序,然后从被排序数组的开头(或者结尾)读入下一个元素,假如这个元素小于buffer中最小的元素,把它写到最开头的空位上;假如这个元素大于buffer中最大的元素,则写到最后的空位上;否则把buffer中最大或者最小的元素写入数组,并把这个元素放在buffer里。保持最大值低于这些关键数据,最小值高于这些关键数据,从而避免对已经有序的中间的数据进行重排。完成后,数组的中间空位必然空出,把这个buffer写入数组中间空位。然后递归地对外部更小的部分,循环地对其他部分进行排序。
三路基数快排
(Three-way Radix Quicksort,也称作Multikey Quicksort、Multi-key Quicksort):结合了基数排序(radix sort,如一般的字符串比较排序就是基数排序)和快排的特点,是字符串排序中比较高效的算法。该算法被排序数组的元素具有一个特点,即multikey,如一个字符串,每个字母可以看作是一个key。算法每次在被排序数组中任意选择一个元素作为关键数据,首先仅考虑这个元素的第一个key(字母),然后把其他元素通过key的比较分成小于、等于、大于关键数据的三个部分。然后递归地基于这一个key位置对“小于”和“大于”部分进行排序,基于下一个key对“等于”部分进行排序。
堆排序
堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于等于(或者大于等于)它的父节点。
每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;
或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
堆具有完全二叉树的概念:
即:树的叶子节点必须从左向右依次补充!中间不能有空叶子!
用数组来表示一棵完全二叉树:
arry[]; //不越界的情况下! 【下角标从0开始】
i的左节点:2*i+1;
i的右节点:2*i+2;
i的父节点:(i-1)/2;
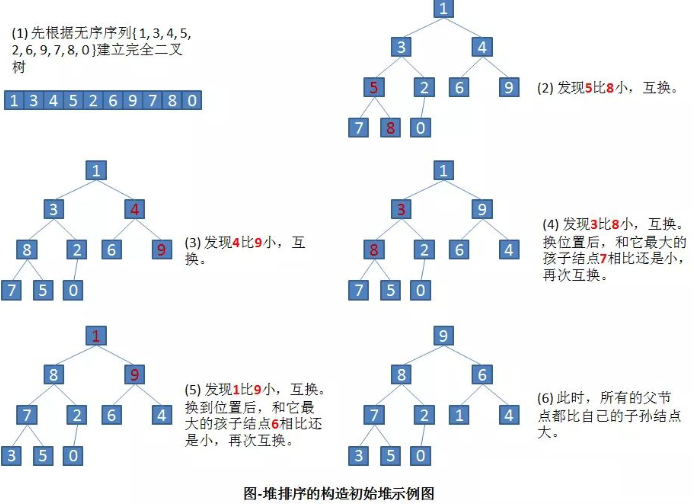
堆排序算法思想:
将向量中存储的数据看成一棵完全二叉树,利用完全二叉树中双亲节点和孩子节点之间的内在关系选择关键字最小的记录。
·将待排序的序列构造成一个大顶堆【或小顶堆】,称为建堆的过程。
·此时,整个序列的最大值【最小值】就是堆顶的根结点。将它移走(其实就是将其与堆数组的末尾元素交换,此时末尾元素就是最大值),即交换v[0], v[n-1]
·然后将剩余的n-1个序列重新构造成一个堆,这样就会得到n个元素中的次大值。
·如此反复执行,直到交换v[0], v[1]。便能得到一个有序序列了。
将一个数组中的数字按大根堆的顺序排列:
(1)换父节点:
遍历数组,比较array[i]与其父节点array[(i-1)/2 ]的大小,若大于父节点,则与父节点交换,并且同样向回比,比较父节点与祖父节点的大小,知道头部。。。。
(2)换子节点:
在准备将数字加入树之前,与自己未来的孩子比较。
即,当array[i]准备入树时,找到自己的两个孩子,array[2*i+1],array[2*i+2],与孩子中最大的值进行比较,若自己小于孩子中的最大值,则交换!然后孩子继续与自己的孩子比较!
大根堆排序:
1 //向下调整 2 void downAdjust(int L, int R) 3 { 4 int i = L, j = 2 * L + 1;//i为父节点,j为左子节点 5 while (j <= R) 6 { 7 if (j + 1 <= R && v[j + 1] > v[j])//若有右节点,且右节点大,那么就选右节点,即选取最大的子节点与父节点对比 8 ++j;//选取了右节点 9 if (v[j] <= v[i])//孩子节点都比父节点小,满足条件,无需调整 10 break; 11 //不满足的话,那么我就将最大孩子节点j与父节点i对调, 12 swap(v[i], v[j]); 13 i = j; 14 j = 2 * i + 1;//继续向下遍历 15 } 16 } 17 //建堆 18 void createHeap() 19 { 20 for (int i = n / 2; i >= 0; --i) 21 downAdjust(i, n - 1); 22 } 23 void HeapSort() 24 { 25 createHeap();//建堆 26 for (int i = n - 1; i > 0; --i)//从最后开始交换,直到只剩下最后一个数字 27 { 28 swap(v[i], v[0]);//每次都将最大值放到最后 29 downAdjust(0, i - 1);//将前0-i个数字重新构成大根堆 30 } 31 }
小根堆排序:
与大根堆排序是一样的【但排序结果为从大到小排序】
只需要在downAdjust()中将父节点与子节点的大小比较改变一下
删除堆顶元素:
1 //删除堆顶元素 2 void deleteTop() 3 { 4 v[0] = v[n - 1];//也就是堆顶使用最后一个数值来替代 5 downAdjust(0, n - 2);//然后对前n-1个数进行排序 6 }
添加元素:
1 //向上调整 2 void upAdjust(int L, int R) 3 { 4 int i = R, j = (i - 1) / 2;//i为欲调整结点,j为其父亲 5 while (j >= L) 6 { 7 if (v[j] < v[i])//父节点小了,那么就将孩子节点调上来 8 { 9 swap(v[i], v[j]); 10 i = j; 11 j = (i - 1) / 2;//继续向上遍历 12 } 13 else//无需调整 14 break; 15 } 16 } 17 void insert(int x) 18 { 19 v[n] = x;//将新加入的值放置在数组的最后,切记保证数组空间充足 20 upAdjust(0, n);//向上调整新加入的结点n 21 }
计数排序
计数排序是一个非基于比较的排序算法,该算法于1954年由 Harold H. Seward 提出。
它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。 当然这是一种牺牲空间换取时间的做法,而且当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序(基于比较的排序的时间复杂度在理论上的下限是O(n*log(n)), 如归并排序,堆排序)
计数排序对输入的数据有附加的限制条件:
1、输入的线性表的元素属于有限偏序集S;
2、设输入的线性表的长度为n,|S|=k(表示集合S中元素的总数目为k),则k=O(n)。
在这两个条件下,计数排序的复杂性为O(n)。
找出待排序的数组中最大和最小的元素;
统计数组中每个值为i的元素出现的次数,存入数组C的第i项;[计数]
对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。[放出去一个,那么就计数减少一个]
计数排序算法是一个稳定的排序算法。
1 void CountSort() 2 { 3 int minN = v[0], maxN = v[0]; 4 for (auto a : v)//找出最大值与最小值 5 { 6 minN = minN < a ? minN : a; 7 maxN = maxN > a ? maxN : a; 8 } 9 vector<int>nums(maxN - minN + 1, 0);//以空间换取时间,用来计算每个数的数量 10 for (auto a : v) 11 ++nums[a - minN]; 12 for (int i = 0, k = 0; i < nums.size(); ++i)//将数赋给原数组 13 while (nums[i]--) 14 v[k++] = i + minN; 15 }
桶排序
桶排序 (Bucket sort)或所谓的箱排序,是一个排序算法,工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序)。
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。
桶排序 (Bucket sort)的工作的原理:
假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排
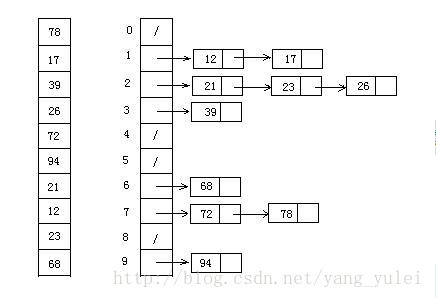
数据结构设计:
链表可以采用很多种方式实现,通常的方法是动态申请内存建立结点,但是针对这个算法,桶里面的链表结果每次扫描后都不同,就有很多链表的分离和重建。如果使用动态分配内存,则由于指针的使用,安全性低。
所以,使用了数组来模拟链表(当然牺牲了部分的空间,但是操作却是简单了很多,稳定性也大大提高了)。共十个桶,所以建立一个二维数组,行向量的下标0—9代表了10个桶,每个行形成的一维数组则是桶的空间。
平均情况下桶排序以线性时间运行。像基数排序一样,桶排序也对输入作了某种假设,因而运行得很快。具体来说,基数排序假设输入是由一个小范围内的整数构成,而桶排序则假设输入由一个随机过程产生,该过程将元素一致地分布在区间[0,1)上。 桶排序的思想就是把区间[0,1)划分成n个相同大小的子区间,或称桶,然后将n个输入数分布到各个桶中去。因为输入数均匀分布在[0,1)上,所以一般不会有很多数落在一个桶中的情况。为得到结果,先对各个桶中的数进行排序,然后按次序把各桶中的元素列出来即可。
在桶排序算法的代码中,假设输入是含n个元素的数组A,且每个元素满足0≤ A[i]<1。
另外还需要一个辅助数组B[O..n-1]来存放链表实现的桶,并假设可以用某种机制来维护这些表。
算法思想:
人为设置一个BucketSize,作为每个桶所能放置多少个不同数值(例如当BucketSize==5时,该桶可以存放{1,2,3,4,5}这几种数字,但是容量不限,即可以存放100个3);
遍历输入数据,并且把数据一个一个放到对应的桶里去;
对每个不是空的桶进行排序,可以使用其它排序方法,也可以递归使用桶排序;
从不是空的桶里把排好序的数据拼接起来。
注意,如果递归使用桶排序为各个桶排序,则当桶数量为1时要手动减小BucketSize增加下一循环桶的数量,否则会陷入死循环,导致内存溢出。
对N个关键字进行桶排序的时间复杂度分为两个部分:
(1) 循环计算每个关键字的桶映射函数,这个时间复杂度是O(N)。
(2) 利用先进的比较排序算法对每个桶内的所有数据进行排序,其时间复杂度为 ∑ O(Ni*logNi) 。
其中Ni 为第i个桶的数据量。
很显然,第(2)部分是桶排序性能好坏的决定因素。尽量减少桶内数据的数量是提高效率的唯一办法(因为基于比较排序的最好平均时间复杂度只能达到O(N*logN)了)。
因此,我们需要尽量做到下面两点:
(1) 映射函数f(k)能够将N个数据平均的分配到M个桶中,这样每个桶就有[N/M]个数据量。
(2) 尽量的增大桶的数量。极限情况下每个桶只能得到一个数据,这样就完全避开了桶内数据的“比较”排序操作。 当然,做到这一点很不容易,数据量巨大的情况下,f(k)函数会使得桶集合的数量巨大,空间浪费严重。这就是一个时间代价和空间代价的权衡问题了。
对于N个待排数据,M个桶,平均每个桶[N/M]个数据的桶排序平均时间复杂度为:
O(N)+O(M*(N/M)*log(N/M))=O(N+N*(logN-logM))=O(N+N*logN-N*logM)
当N=M时,即极限情况下每个桶只有一个数据时。桶排序的最好效率能够达到O(N)。
总结:桶排序的平均时间复杂度为线性的O(N+C),其中C=N*(logN-logM)。如果相对于同样的N,桶数量M越大,其效率越高,最好的时间复杂度达到O(N)。当然桶排序的空间复杂度为O(N+M),如果输入数据非常庞大,而桶的数量也非常多,则空间代价无疑是昂贵的。此外,桶排序是稳定的。
1 void BucketSort() 2 { 3 int minN = v[0], maxN = v[0]; 4 for (auto a : v)//找出最大值与最小值 5 { 6 minN = minN < a ? minN : a; 7 maxN = maxN > a ? maxN : a; 8 } 9 vector<vector<int>>bucket((maxN-minN)/10+1);//除数是按照数据范围进行调整的 10 for (auto a : v)//将数据放入对应的桶中 11 bucket[(a - minN) / 10].push_back(a); 12 for (int i = 0; i < bucket.size(); ++i) 13 sort(bucket[i].begin(), bucket[i].end());//分别对每个桶进行排序,可以使用任意的排序算法,个人感觉没必要使用复杂的排序算法 14 int k = 0; 15 for (auto a : bucket)//将数据赋予原数组 16 for (auto b : a) 17 v[k++] = b; 18 }
基数排序
基数排序(radix sort)属于“分配式排序”(distribution sort),基数排序也是非比较的排序算法,对每一位进行排序,从最低位开始排序,复杂度为O(kn),为数组长度,k为数组中的数的最大的位数;
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以是稳定的。
过程:
取得数组中的最大数,并取得位数;
arr为原始数组,从最低位开始取每个位组成radix数组;
对radix进行计数排序(利用计数排序适用于小范围数的特点);
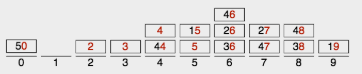
源数据:

第一次排序:【按个位数】
还原:【底下的先出来】

再排:【按十位数】
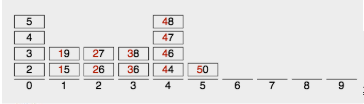
再次还原:【底下的先出来】

最高位优先(Most Significant Digit first)法,简称MSD法:先按k1排序分组,同一组中记录,关键码k1相等,再对各组按k2排序分成子组,之后,对后面的关键码继续这样的排序分组,直到按最次位关键码kd对各子组排序后。再将各组连接起来,便得到一个有序序列。
最低位优先(Least Significant Digit first)法,简称LSD法:先从kd开始排序,再对kd-1进行排序,依次重复,直到对k1排序后便得到一个有序序列。
1 //基数排序 2 void RadixSort() 3 { 4 int maxBit = 0;//最大的位数 5 int bit = 1;//先从个位开始 6 for (auto a : v) 7 { 8 int len = to_string(a).length();//这里我就偷懒直接使用string来转换 9 maxBit = maxBit > len ? maxBit : len; 10 } 11 for (int i = 1; i <= maxBit; ++i)//最大的数有多少位就进行多少次排序 12 { 13 vector<vector<int>>count(10);//存放位数上数值相同的数据 14 for (auto a : v) 15 count[(a % (bit * 10) / bit)].push_back(a);//按照第bit位上进行排序 16 int k = 0; 17 for (auto a : count) 18 for (auto b : a) 19 v[k++] = b;//将数据放回 20 bit *= 10;//向前一位 21 } 22 }
排序算法总结:
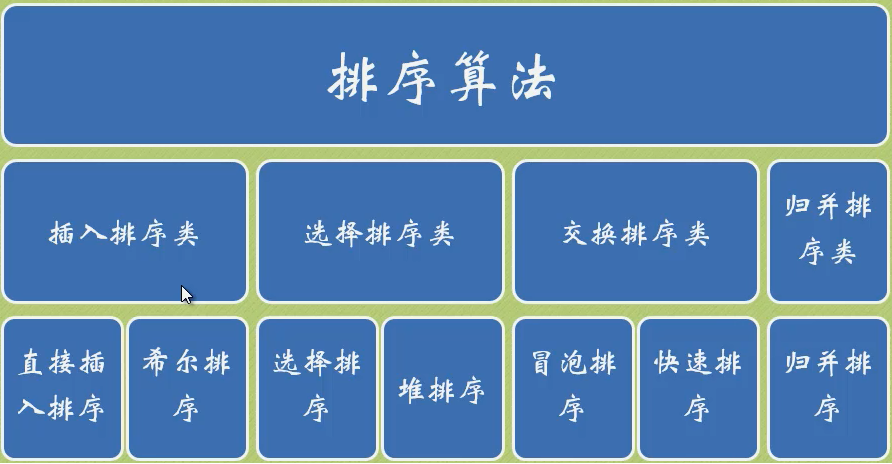
·比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
·非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
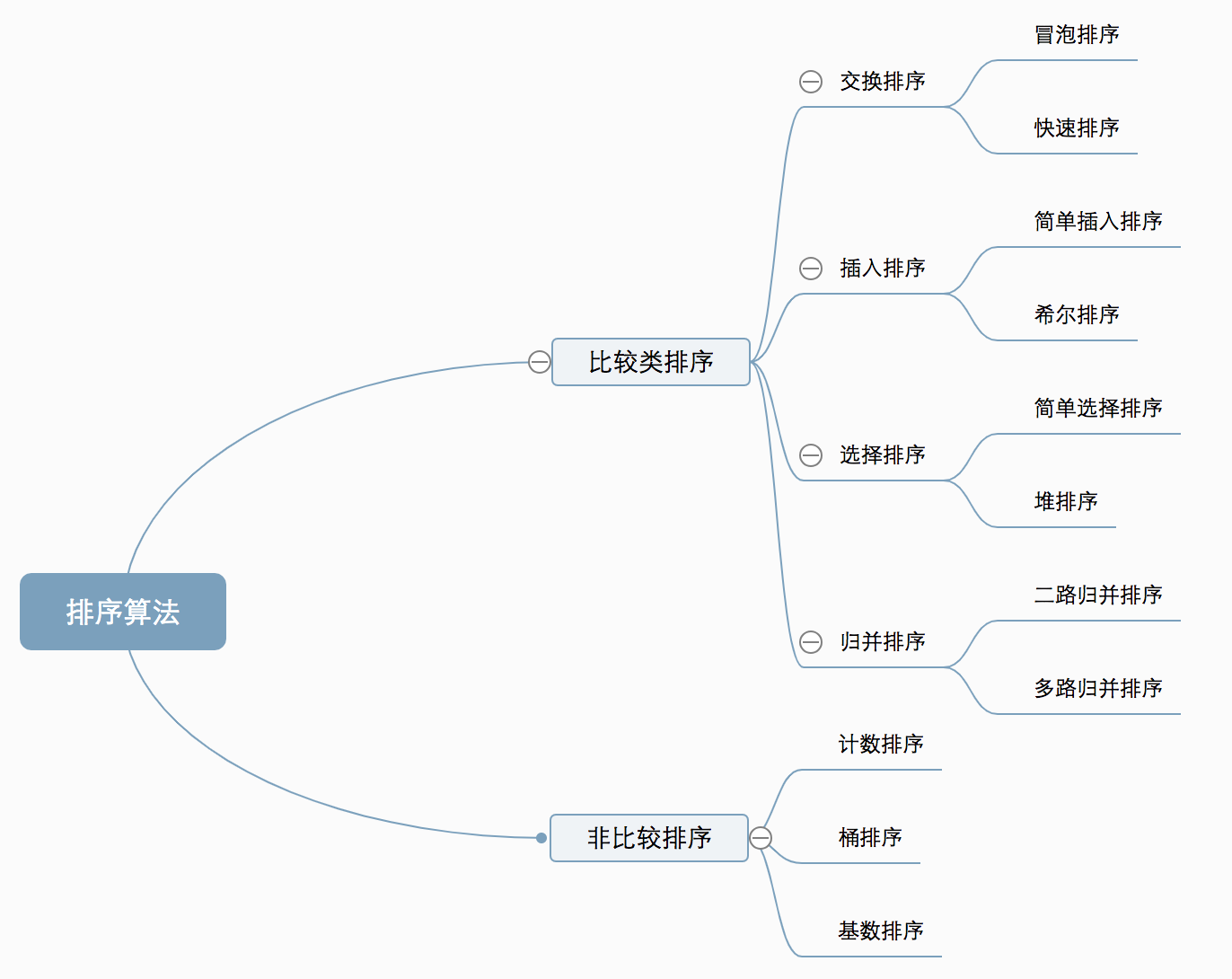

名词及数据解释:
·n: 数据规模
·k: “桶”的个数
·In-place: 占用常数内存,不占用额外内存
·Out-place: 占用额外内存
·log为log2
·稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
·不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
·时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
·空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
从算法的简单性来看,我们将7种算法分为两类:
·简单算法:冒泡、简单选择、直接插入。
·改进算法:希尔、堆、归并、快速。
·比较排序:快速排序、归并排序、堆排序、冒泡排序。
在排序的最终结果里,元素之间的次序依赖于它们之间的比较。每个数都必须和其他数进行比较,才能确定自己的位置。
·非比较排序:计数排序、基数排序、桶排序
- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面;
- 不稳定:如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面;
- 内排序:所有排序操作都在内存中完成;
- 外排序:由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行;
- 时间复杂度: 一个算法执行所耗费的时间。
- 空间复杂度:运行完一个程序所需内存的大小。
所谓的稳定性:
就是维持相同数字在排序过程中的相对位置。
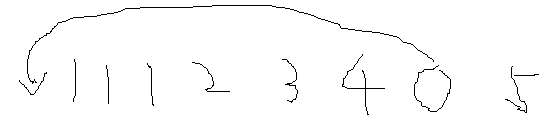
是稳定的,以为111的相对位置未被打乱。

不是稳定的,因为555的相对位置打乱了。
意义:
在比较数据的属性时,比如年龄、身高、体重
若按身高排序,然后再按年龄排序,在稳定性下,相同年龄的两人会安上次身高的排序放置!!!
怎么选用排序算法
·在排序数据<60时,会选择插入排序,当数据量很大时,先选择归并等算法,当数据分支小于60时,立马使用插入排序。
·从空间复杂度来考虑:首选堆排序,其次是快速排序,最后是归并排序。
·若从稳定性来考虑,应选取归并排序,因为堆排序和快速排序都是不稳定的。
·若从平均情况下的排序速度考虑,应该选择快速排序。