Dijkstra算法

Djkstra算法示例演示

下面我求下图，从顶点v1到其他各个顶点的最短路径

 

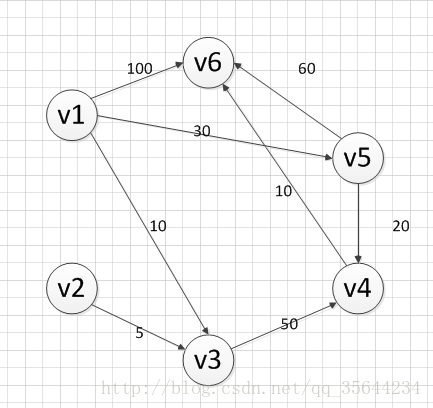
首先第一步，我们先声明一个dis数组，该数组初始化的值为:

 

 

我们的顶点集T的初始化为：T={v1}

既然是求 v1顶点到其余各个顶点的最短路程，那就先找一个离 1 号顶点最近的顶点。通过数组 dis 可知当前离v1顶点最近是 v3顶点。当选择了 2 号顶点后，dis[2]（下标从0开始）的值就已经从“估计值”变为了“确定值”，即 v1顶点到 v3顶点的最短路程就是当前 dis[2]值。将V3加入到T中。

为什么呢？因为目前离 v1顶点最近的是 v3顶点，并且这个图所有的边都是正数，那么肯定不可能通过第三个顶点中转，使得 v1顶点到 v3顶点的路程进一步缩短了。因为 v1顶点到其它顶点的路程肯定没有 v1到 v3顶点短.

OK，既然确定了一个顶点的最短路径，下面我们就要根据这个新入的顶点V3会有出度，发现以v3 为弧尾的有： < v3,v4 >,那么我们看看路径：v1–v3–v4的长度是否比v1–v4短，其实这个已经是很明显的了，因为dis[3]代表的就是v1–v4的长度为无穷大，而v1–v3–v4的长度为：10+50=60，所以更新dis[3]的值,得到如下结果：

 

因此 dis[3]要更新为 60。这个过程有个专业术语叫做“松弛”。即 v1顶点到 v4顶点的路程即 dis[3]，通过 < v3,v4> 这条边松弛成功。这便是 Dijkstra 算法的主要思想：通过“边”来松弛v1顶点到其余各个顶点的路程。

然后，我们又从除dis[2]和dis[0]外的其他值中寻找最小值，发现dis[4]的值最小，通过之前是解释的原理，可以知道v1到v5的最短距离就是dis[4]的值，然后，我们把v5加入到集合T中，然后，考虑v5的出度是否会影响我们的数组dis的值，v5有两条出度：< v5,v4>和 < v5,v6>,然后我们发现：v1–v5–v4的长度为：50，而dis[3]的值为60，所以我们要更新dis[3]的值.另外，v1-v5-v6的长度为：90，而dis[5]为100，所以我们需要更新dis[5]的值。更新后的dis数组如下图：

 

然后，继续从dis中选择未确定的顶点的值中选择一个最小的值，发现dis[3]的值是最小的，所以把v4加入到集合T中，此时集合T={v1,v3,v5,v4},然后，考虑v4的出度是否会影响我们的数组dis的值，v4有一条出度：< v4,v6>,然后我们发现：v1–v5–v4–v6的长度为：60，而dis[5]的值为90，所以我们要更新dis[5]的值，更新后的dis数组如下图：

  

然后，我们使用同样原理，分别确定了v6和v2的最短路径，最后dis的数组的值如下：

 

因此，从图中，我们可以发现v1-v2的值为：∞，代表没有路径从v1到达v2。所以我们得到的最后的结果为：

起点  终点    最短路径    长度

v1    v2     无          ∞    

      v3     {v1,v3}    10

      v4     {v1,v5,v4}  50

      v5     {v1,v5}    30

      v6     {v1，v5,v4,v6} 60

 代码：

　　版本一：与图解匹配

void Test01()
{
    createDis();
    vector<int>pathNum(Size, 0);//用来保存最优路径数量
    vector<int>path(Size, Start);//每个的点的上溯点是哪个点，用来找出最优路线图
    vector<bool>index(Size, true);//用来标记是否已经遍历过的点
    pathNum[Start] = 1;//最开始初始化有一条
    index[Start] = false;
    int first = 1;
    //在city[Start]的基础上对city[Start][End]的最短距离，第一个出发点不是Start
    for (int i = 0; i < Size; ++i)
    {
        //先找出发点去往下一个最近的点
        int p = -1;
        int minD = INF;
        for (int j = 0; j < Size; ++j)
        {
            if (index[j] && minD > city[Start][j])
            {
                p = j;
                minD = city[Start][j];
                if (first)
                {
                    pathNum[p] = 1;
                    first = 0;
                }
            }
        }
        if (p == -1)
            break;//遍历完毕
        index[p] = false;//已经遍历过了
        //那么就遍历点p能去往的点
        for (int j = 0; j < Size; ++j)
        {
            //更新点Start->j的距离
            if (index[j] && city[Start][j] > city[Start][p] + city[p][j])
            {
                city[Start][j] = city[Start][p] + city[p][j];
                path[j] = p;//更新路径记录，即到达j的最优路径是经过点p的    
                pathNum[j] = pathNum[p];
            }
            else if (index[j] && city[Start][j] == city[Start][p] + city[p][j])//出现相同路径
            {
                pathNum[j] += pathNum[p];//叠加最优路径数量
            }
        }
    }
    cout << "最短路径为：" << city[Start][End] << endl;
    cout << "最优路径数量为：" << pathNum[End] << endl;
    int  k = End;
    //最优路线是反着的，如果要顺着，则使用栈再存一次，这里就不做了
    cout << "最优路线为：" << endl << k << "->";
    while (k!=Start)
    {
        k = path[k];
        cout << k << "->";
    }
    cout << endl;

}

　　版本二：只有一点点改变，就是从出发点开始遍历

void Test02()
{
    createDis();
    vector<int>pathNum(Size, 0);//用来保存最优路径数量
    vector<int>path(Size, Start);//每个的点的上溯点是哪个点，用来找出最优路线图
    vector<bool>index(Size, true);//用来标记是否已经遍历过的点
    vector<int>Dis(Size, INF);
    pathNum[Start] = 1;//最开始初始化有一条
    Dis[Start] = 0;//Start开始出发

    //与Test01不同的是，此处在Dis的基础上进行距离更新，第一次出发点一定是Start
    for (int i = 0; i < Size; ++i)
    {
        //先找出发点去往下一个最近的点
        int p = -1;
        int minD = INF;
        for (int j = 0; j < Size; ++j)
        {
            if (index[j] && minD > city[Start][j])
            {
                p = j;
                minD = city[Start][j];
            }
        }
        if (p == -1)
            break;//遍历完毕
        index[p] = false;//已经遍历过了
        //那么就遍历点p能去往的点
        for (int j = 0; j < Size; ++j)
        {
            //更新点Start->j的距离
            if (index[j] && city[Start][j] > city[Start][p] + city[p][j])
            {
                city[Start][j] = city[Start][p] + city[p][j];
                path[j] = p;//更新路径记录，即到达j的最优路径是经过点p的    
                pathNum[j] = pathNum[p];
            }
            else if (index[j] && city[Start][j] == city[Start][p] + city[p][j])//出现相同路径
            {
                pathNum[j] += pathNum[p];//叠加最优路径数量
            }
        }
    }
    cout << "最短路径为：" << city[Start][End] << endl;
    cout << "最优路径数量为：" << pathNum[End] << endl;
    int  k = End;
    //最优路线是反着的，如果要顺着，则使用栈再存一次，这里就不做了
    cout << "最优路线为：" << endl << k << "->";
    while (k != Start)
    {
        k = path[k];
        cout << k << "->";
    }
    cout << endl;
}

　　其他：

#include <iostream>
#include <vector>

using namespace std;

#define INF 999999
#define Size 9
vector<vector<int>>city(Size, vector<int>(Size, INF));//将距离矩
阵初始化为0

int Start = 0, End = 8;
void createDis()
{
    //一般是输入的，这里就直接初始化了
    city.clear();//清除
    city.push_back({ 0,        1,        5,        INF,    INF,    INF,    INF,    INF,    INF});
    city.push_back({ 1,        0,        3,        7,        5,        INF,    INF,    INF,    INF});
    city.push_back({ 5,        3,        0,        INF,    1,        7,        INF,    INF,    INF});
    city.push_back({ INF,    7,        INF,    0,        2,        INF,    3,        INF,    INF });
    city.push_back({ INF,    5,        1,        2,        0,        3,        6,        9,        INF});
    city.push_back({ INF,    INF,    7,        INF,    3,        0,        INF,    5,        INF});
    city.push_back({ INF ,    INF,    INF,    3,        6,        INF,    0,        2,        7});//7
    city.push_back({ INF ,    INF,    INF,    INF,    9,        5,        2,        0,        4});
    city.push_back({ INF ,    INF,    INF,    INF,    INF,    INF,    7,        4,        0 });
}


int main()
{
    Test01();
    Test02();
    return 0;
}