力扣算法题—084柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

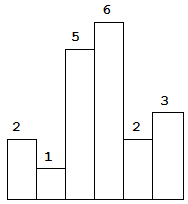
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

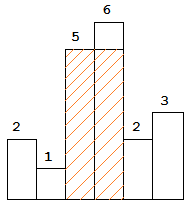
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

在真实的面试中遇到过这道题？

 

 

#include "_000库函数.h"

//头尾指针，然后在寻找头尾指针中间最短的值
//貌似复杂度为n^2有点高
//超出时间限制
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        if (heights.empty())return 0;
        if (heights.size() == 1)return heights[0];
        int max = -1;
        for (int left = 0; left < heights.size(); ++left) {
            int min = heights[left];
            for (int right = left; right < heights.size(); ++right) {
                min = min < heights[right] ? min : heights[right];
                max = max > (min*(right - left + 1)) ? max : (min*(right - left + 1));
            }                
        }        
        return max;
    }
};


//使用局部峰值，即该数大于后一个数就是局部峰值，
//然后遍历前面所有的数字

// Pruning optimize
class Solution {
public:
    int largestRectangleArea(vector<int> &height) {
        int res = 0;
        for (int i = 0; i < height.size(); ++i) {
            if (i + 1 < height.size() && height[i] <= height[i + 1]) {
                continue;
            }
            int minH = height[i];
            for (int j = i; j >= 0; --j) {
                minH = min(minH, height[j]);
                int area = minH * (i - j + 1);
                res = max(res, area);
            }
        }
        return res;
    }
};

//使用栈
//栈只存放数字下角标
//遇到比栈顶的数小的数则拿出来进行处理
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int res = 0;
        stack<int> st;
        heights.push_back(0);
        for (int i = 0; i < heights.size(); ++i) {
            while (!st.empty() && heights[st.top()] >= heights[i]) {
                int cur = st.top(); 
                st.pop();
                res = max(res, heights[cur] * (st.empty() ? i : (i - st.top() - 1)));
            }
            st.push(i);
        }
        return res;
    }
};

void T084() {
    Solution s;
    vector<int>v;
    v = { 2,1,5,6,2,3 };
    cout << s.largestRectangleArea(v) << endl;
    v = { 0,9};
    cout << s.largestRectangleArea(v) << endl;
}