这篇博客主要讲几种常见的集成学习方法:bagging, boosting, stacking。
简介
这一小节先简单讲讲这几种集成学习方法的思路,这几种方法的思路其实是很简单的。
bagging,是 Bootstrap aggregating 的简称,它使用了自主采样法(Boostrap)。从训练集采样出 (n) 个子集,分别对这 (n) 个子集进行训练,得到 (n) 个基学习器。对于分类问题,可以由这 (n) 个基学习器投票得出结果;对于回归问题,可以由这 (n) 个基学习器平均输出得到结果。采样、训练的过程是可以并行进行的,这个方法很容易就并行化了。
boosting,这里引用 Wikipedia[4] 的说法,boosting 是一族将弱学习器转化为强学习器的算法,boosting 来源于一个问题: "Can a set of weak learners create a single strong learner?"。因此,那些将弱学习器转化为强学习器的一类算法都可以算是 boosting。
stacking,和它的名字一样,将多个基学习器像栈一样堆叠起来。stacking 一般分成两层,第一层的输入是训练集。第二层的输入是第一层多个学习器的预测结果。
bagging
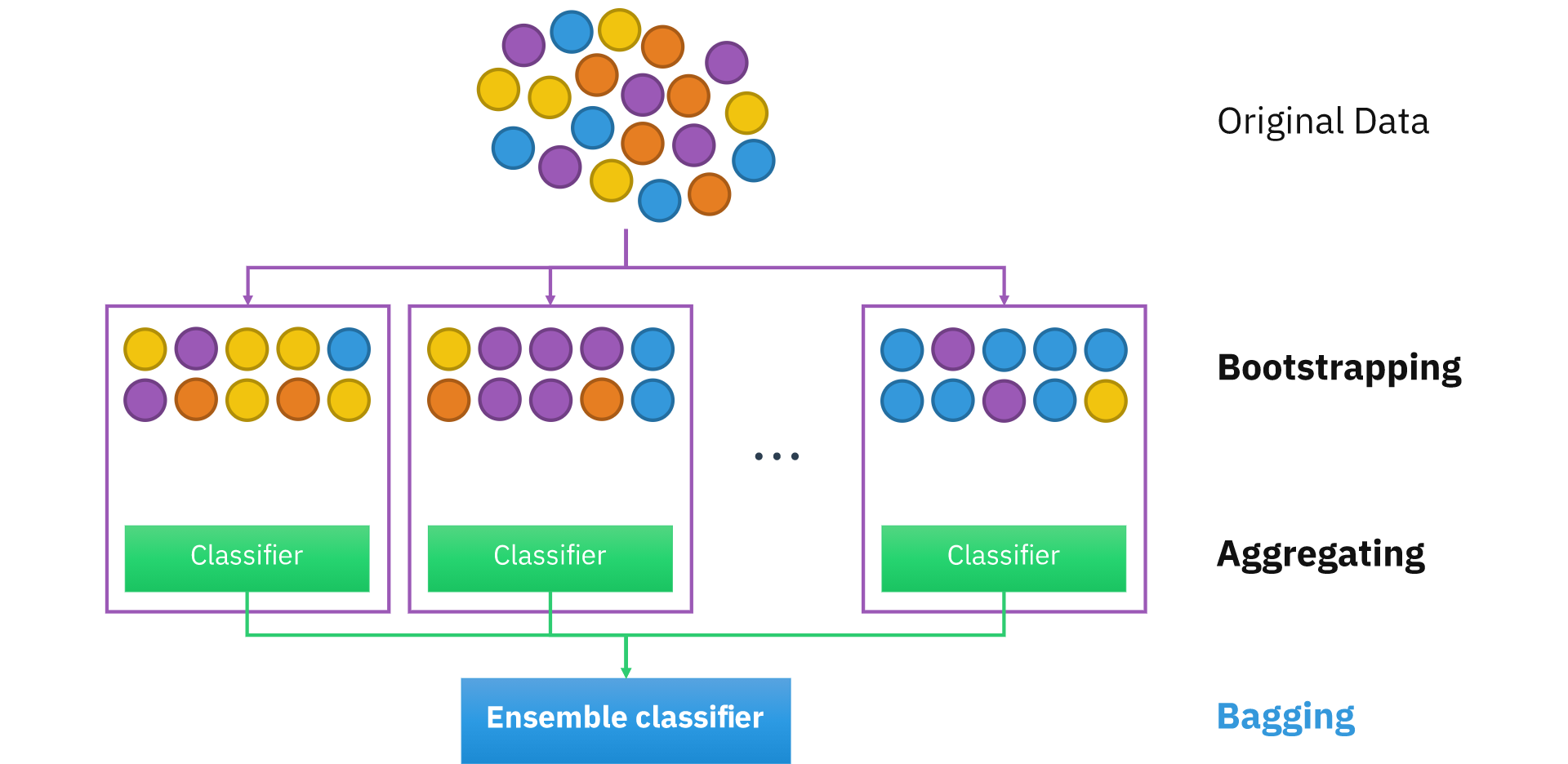
集成学习集成的就是一些“好而不同”的基学习器,在 bagging 中,如何产生这些“好而不同”的基学习器呢?方法是,对训练集进行采样,产生了不同的子集,这些不同的子集学习产生的基学习器在一定程度上会存在差异。“好而不同”,这就是为什么 bagging 要采样产生数据集的子集来训练的原因。
自助采样法
采样方法:有放回的采样 (|D|) 次,(|D|) 表示数据集大小。
这个自助采样法在 [2] 中提出的地方,讲的是训练集和测试集划分的问题,它旨在寻找一种可以较好评估模型的方法。
随机森林
随机森林,是用了决策树作为基学习器的 bagging。此外,在决策树生成的过程中,每次选择最优划分属性之前,都要随机选择 (k) 个的属性子集,从这 (k) 个属性中选出最优划分属性。
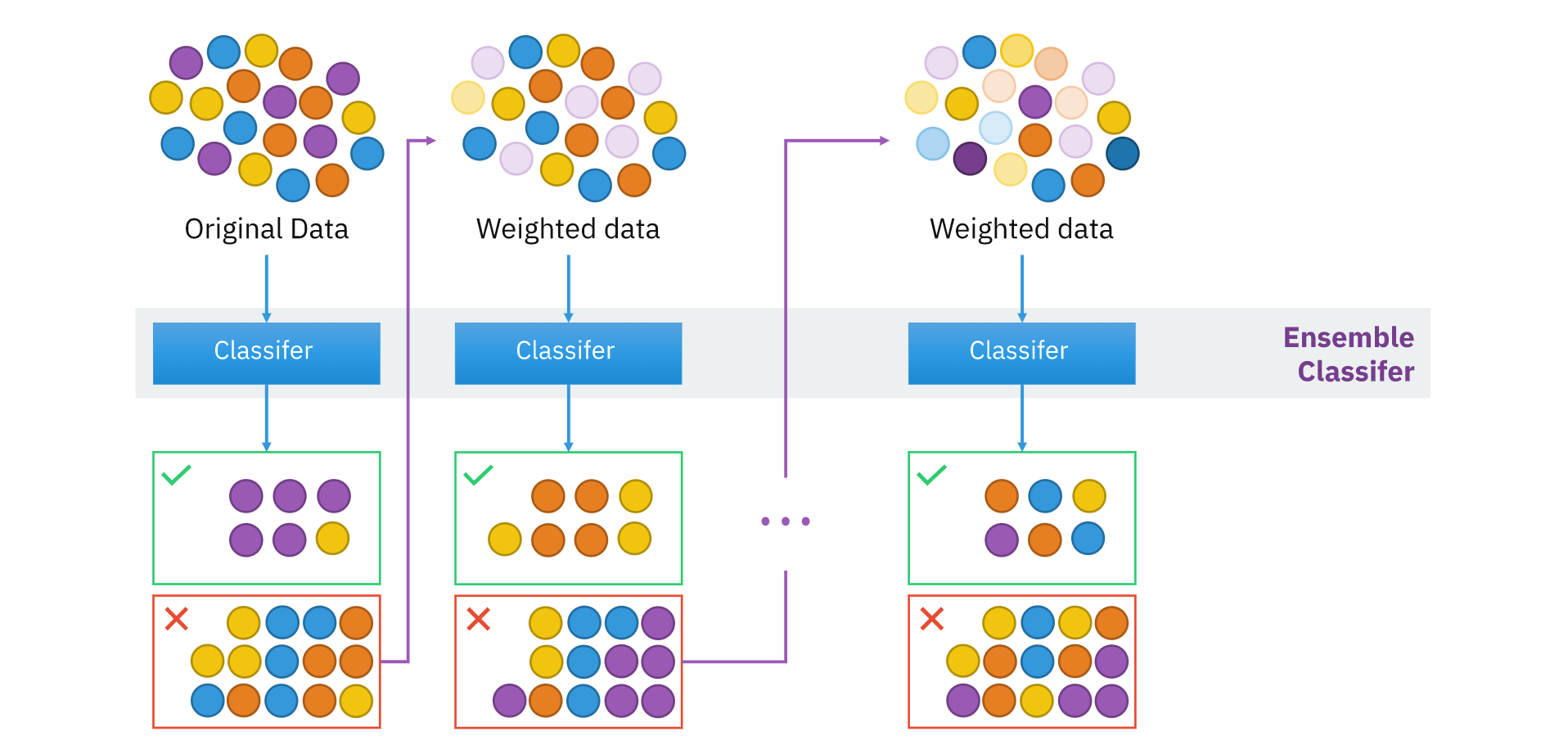
boosting
这个小节主要介绍 adaboost,提升树和前向分步算法将会在写在另一篇博客中。对于 adaboost,使用整个训练集来训练一个基学习器,再使用基学习器对整个数据集做预测,根据预测结果的正误,我们可以加大错误样本的权重,减小正确样本的权重。之后再重新学习一个基学习器,如此进行学习 (n) 个基学习器。最后预测的结果由这 (n) 个基学习器加权计算得到结果,权重的计算可以使用基学习器在训练集上的正确率来计算。由于每个学习器的样本权重依赖于上一个样本的权重,所以这个过程必须是一个一个地进行的。
[2] 中描述的算法如下图所示,书里主要介绍了 adaboost 算法。初始情况下,所有样本的权重一样大,所有样本都受到相同的关注。第 3 行,是学习出来的预测函数,第 4 行是这个预测函数预测的错误率。如果这个错误率大于 0.5,也就是比瞎猜还要差,那么就退出,不能让他参与到最终的决策。第 6 行,计算这个基学习器的比重,在最后预测的时候,使用加权求和来进行预测。第 7 行,更新样本的权值,让那些分类错误的样本受到更多的关注。

stacking
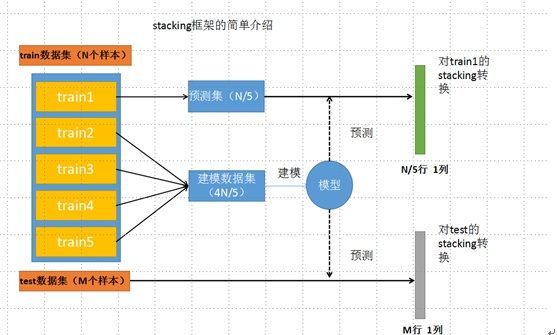
这里从 [3] 那里盗一张图,未经原作者允许,侵删。我觉得这张图讲的最清楚不过了。
stacking 一般和交叉验证一起来用,目的是为了防止过拟合。将训练集分为 (K) 折,其中的一折拿来做验证集,剩下的拿来训练第一层的基学习器。假如我们有 (n) 个基学习器,基学习器学习好了之后,对那一折的一个样本做预测,我们可以得到一个 (n) 维向量,将这些 (n) 维向量作为第二层学习器的输入。一般来说,第二层的学习器使用 LR 就可以了。
Question
Q: adaboost 的(alpha) 和权值如何推导出来的?
A: 这个得看前向分步算法。
Q: 提升树和 boosting 什么关系呢?它似乎没有改变样本的权重。
A: 有这个问题,说明混淆了 boosting 和 boosting 的具体实现。改变样本权重来再次训练基学习器,是 boosting 的一个思路。boosting 来自于 [4] 提到的 "Can a set of weak learners create a single strong learner?",boosting 旨在将弱学习器转为强学习器。提升树做的也是这个事情,将弱的决策树提升,组合成为一个更强的预测函数。
Q: 为什么说 stacking 容易过拟合,交叉验证如何避免过拟合?
A: 还有待思考。。。
[1] 李航统计学习方法
[2] 周志华机器学习
[3] https://zhuanlan.zhihu.com/p/31961233
[4] https://en.wikipedia.org/wiki/Boosting_(machine_learning)