1.本节重点知识点用自己的话总结出来,可以配上图片,以及说明该知识点的重要性
本节课讲了线性回归算法的相关的知识,回顾了与线性回归相关的线性代数、高等数学的知识,进入了线性回归的学习,介绍了线性回归算法的研究背景。
回顾了这些知识才能继续后面学习,有助于加快理解后面的概念。
介绍讲解了线性回归的定义。从理论公式入手理解算法更有指导性和依据。
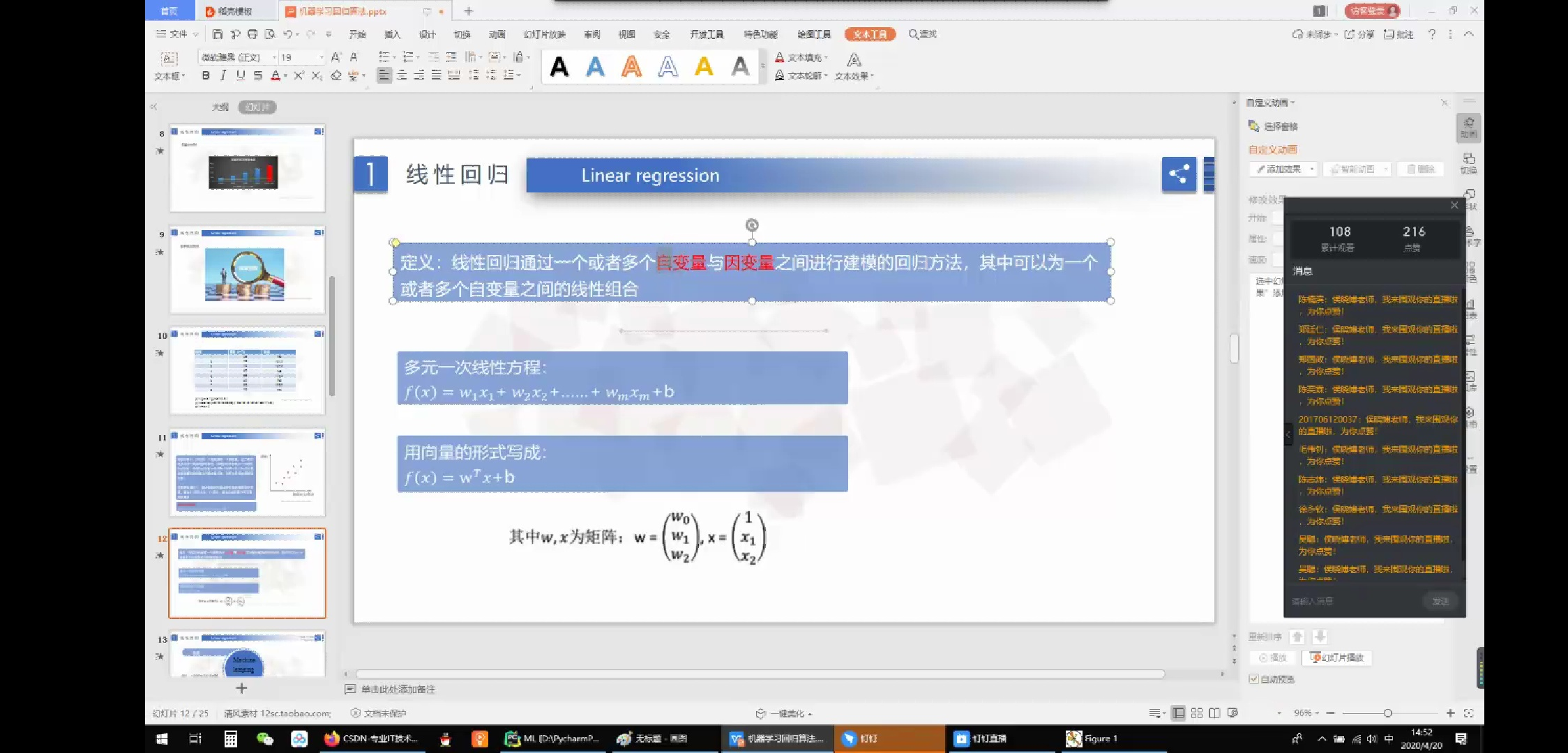
讲解了回归和分类的区别。了解了区别能明白它们的不同,有不同的应用场景。
学习了损失函数的概念以及作用。引入损失函数的概念,可以帮助我们更好的理解误差。
2.思考线性回归算法可以用来做什么?(大家尽量不要写重复)
线性回归算法将数据拟合出一条直线出来,线性算法的实现是计算出直线与离散数据的疏密程度。线性回归算法的应用场景有:电影观影人数的预测;社交平台粉丝互动量预测;根据天气预测人们生产活动和购物的趋势;新闻关键词热度的预测;体育比赛球队胜率的预测;根据人流量预测交通是否堵塞。
3.自主编写线性回归算法 ,数据可以自己造,或者从网上获取。(加分题)
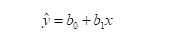
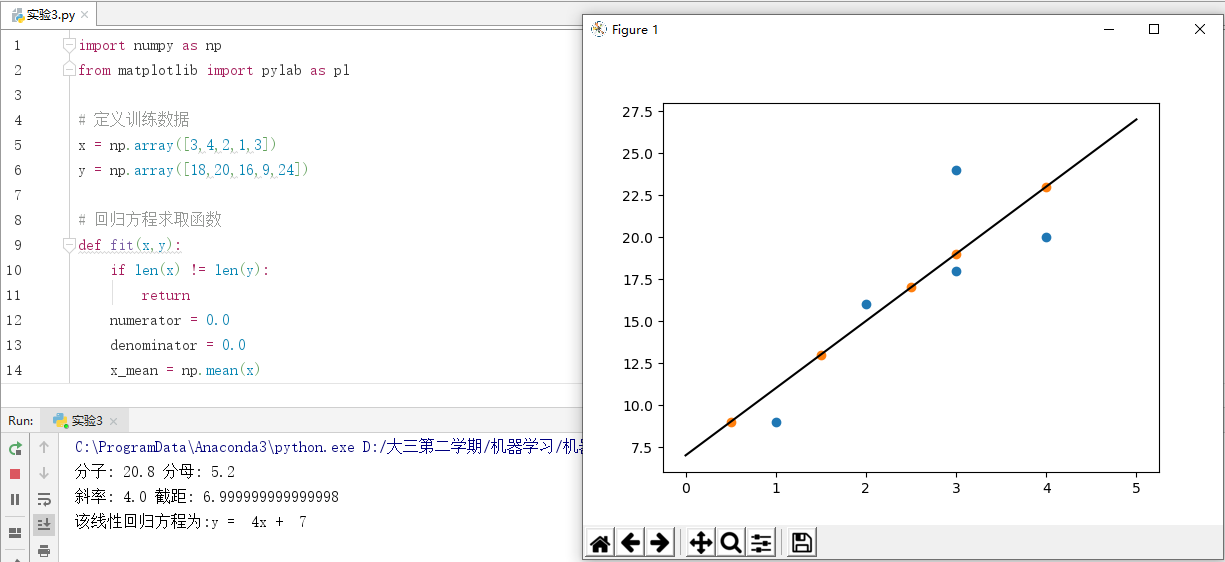
用Python实现线性回归方程的求解,实现代码如下:
import numpy as np from matplotlib import pylab as pl # 定义训练数据 x = np.array([3,4,2,1,3]) y = np.array([18,20,16,9,24]) # 回归方程求取函数 def fit(x,y): if len(x) != len(y): return numerator = 0.0 denominator = 0.0 x_mean = np.mean(x) y_mean = np.mean(y) for i in range(len(x)): numerator += (x[i]-x_mean)*(y[i]-y_mean) denominator += np.square((x[i]-x_mean)) print('分子:',numerator,'分母:',denominator) b0 = numerator/denominator b1 = y_mean - b0*x_mean print('斜率:', b0, '截距:', b1) return b0,b1 # 定义预测函数 def predit(x,b0,b1): return b0*x + b1 # 求取回归方程 b0,b1 = fit(x,y) print('该线性回归方程为:y = %2.0fx + %2.0f'%(b0,b1)) # 预测 x_test = np.array([0.5,1.5,2.5,3,4]) y_test = np.zeros((1,len(x_test))) for i in range(len(x_test)): y_test[0][i] = predit(x_test[i],b0,b1) # 绘制图像 xx = np.linspace(0, 5) yy = b0*xx + b1 pl.plot(xx,yy,'k-') pl.scatter(x,y,cmap=pl.cm.Paired) pl.scatter(x_test,y_test[0],cmap=pl.cm.Paired) pl.show()
运行结果:
分子: 20.8 分母: 5.2
斜率: 4.0 截距: 6.999999999999998
该线性回归方程为:y = 4x + 7
实验截图: