Surround the Trees
Problem Description
There are a lot of trees in an area. A peasant wants to buy a rope to surround all these trees. So at first he must know the minimal required length of the rope. However, he does not know how to calculate it. Can you help him?
The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line.
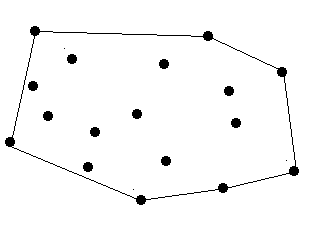
There are no more than 100 trees.
The diameter and length of the trees are omitted, which means a tree can be seen as a point. The thickness of the rope is also omitted which means a rope can be seen as a line.

There are no more than 100 trees.
Input
The input contains one or more data sets. At first line of each input data set is number of trees in this data set, it is followed by series of coordinates of the trees. Each coordinate is a positive integer pair, and each integer is less than 32767. Each pair is separated by blank.
Zero at line for number of trees terminates the input for your program.
Zero at line for number of trees terminates the input for your program.
Output
The minimal length of the rope. The precision should be 10^-2.
Sample Input
9
12 7
24 9
30 5
41 9
80 7
50 87
22 9
45 1
50 7
0
Sample Output
243.06
题意:
简单的凸包模板题目
题解:
这里介绍一种求凸包的算法:Graham。(相对于其它人的解释可能会有一些出入,但大体都属于这个算法的思想,同样可以解决凸包问题)
相对于包裹法的n*m时间,Graham算法在时间上有很大的提升,只要n*log(n)时间就够了。它的基本思想如下:
1、首先,把所有的点按照y最小优先,其次x小的优先排序
2、维护一个栈,用向量的叉积来判断新插入的点跟栈顶的点哪个在外围,如果栈顶的点在当前插入的点的左边,那么把栈顶的这个元素弹出,弹出之后不能继续插入下一个点,要继续判断当前插入点跟弹出之后的栈顶的点的位置关系,当当前插入的点在栈顶的那个点的左边时,则可以将要插入的点压到栈中,进入下一个点。
http://blog.csdn.net/bone_ace/article/details/46239187
#include <iostream> #include <cstdio> #include <cmath> #include <cstring> #include <algorithm> using namespace std; const int N = 1e5+10, M = 30005, mod = 1e9 + 7, inf = 0x3f3f3f3f; typedef long long ll; struct point{ double x,y; point (double x = 0, double y = 0):x(x),y(y) {} friend point operator + (point a,point b) { return point(a.x+b.x,a.y+b.y); } friend point operator - (point a,point b) { return point(a.x-b.x,a.y-b.y); } }p[N],res[N]; double dis(point a,point b) { return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); } double dot(point a,point b) { return a.x*b.y-b.x*a.y; } int cmp(point a,point b) { if(a.y==b.y) return a.x<b.x; else return a.y<b.y; } int Graham(point* p,int n,point* res) { sort(p+1,p+n+1,cmp); res[1] = p[1]; res[2] = p[2]; int top = 2,len; for(int i=3;i<=n;i++) { while(top>=2 && dot(p[i] - res[top-1],res[top] - res[top-1])>=0) top--; res[++top] = p[i]; } len = top; for(int i=n;i>=1;i--) { while(top!=len&&dot(p[i]-res[top-1],res[top]-res[top-1])>=0) top--; res[++top] = p[i]; } return top; } int main() { int n; while(scanf("%d",&n)&&n) { for(int i=1;i<=n;i++) scanf("%lf%lf",&p[i].x,&p[i].y); if(n==1) { printf("0.00 ");continue; } if(n==2) { printf("%.2f ",dis(p[1],p[n])); continue; } int m=Graham(p,n,res); double tot=0; for(int i=2;i<=m;i++) tot+=dis(res[i-1],res[i]); printf("%.2f ",tot); } }