二维数组求最大子数组的和（连通性）

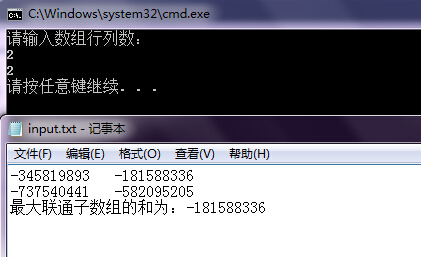
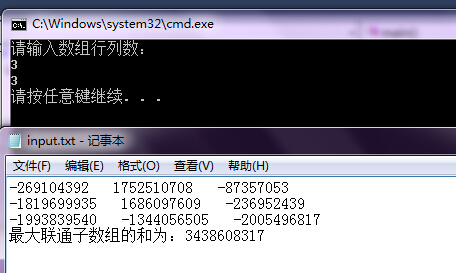
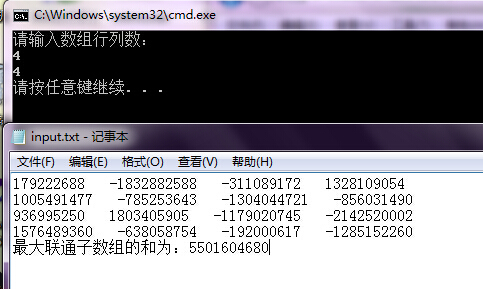
本程序的基本功能是：输入数组的行数和列数，程序自动生成对应规格的数组，在满足连通性的情况下，求最大的子数组的和。

主要的功能的实现是依靠图的遍历。

#include<fstream>
#include<iostream>
#include<ctime>
using namespace std;
#define RAND16 ((rand()<<1) + (rand()&1))
#define N 100
# define WIDE 4294967296
typedef struct
{
    long long int dian[N];
    long long int xian[N][N];
    long long int dianx, xianx;
}A;

void set(A &shu, int x, int y)
{
    shu.dianx = x*y;
    srand((_int32)time(NULL));
    for (int i = 1; i <= shu.dianx; i++)
    {
        shu.dian[i] = (RAND16 << 16) + RAND16;
        if (rand() % 2 == 1)
            shu.dian[i] = shu.dian[i] * (-1);
    }
    for (int i = 1; i <= shu.dianx; i += y)
    {
        for (int j = i; j <= i + y - 2; j++)
        {
            shu.xian[j][j + 1] = 1;
            shu.xian[j + 1][j] = 1;
        }
    }
    for (int i = 1 + y; i<shu.dianx; i += y)
    {
        for (int j = i; j <= i + x - 1; j++)
        {
            shu.xian[j][j - y] = 1;
            shu.xian[j - y][j] = 1;
        }
    }
}

void bianli(A &shu, long long int v, long long int visit[], long long int &b, long long int &max, long long int x)
{
    visit[v] = 1;

    max += shu.dian[v];
    if (max >= b)
        b = max;

    int a = 0, bo = 0;
    for (int w = 1; w <= shu.dianx; w++)
    {
        for (int c = 1; c <= shu.dianx; c++)
        {
            if ((visit[w] == 0) && (shu.xian[c][w] == 1) && (visit[c] == 1))
            {
                a = w; bo = 1; break;
            }
        }
        if (bo == 1)
            break;
    }
    for (int w = 1; w <= shu.dianx; w++)
    {
        for (int c = 1; c <= shu.dianx; c++)
        {
            if ((visit[w] == 0) && (shu.xian[c][w] == 1) && (visit[c] == 1))
            {
                if (shu.dian[a]<shu.dian[w])
                    a = w;
            }
        }
    }
    if (b + shu.dian[a]<0)
    {
        shu.xian[v][a] = 0;
    }
    else
        bianli(shu, a, visit, b, max, x);
}

int NoVisit(long long int visit[], A shu)
{
    int k = 0, i;
    for (i = 1; i <= shu.dianx; i++)
    {
        if (visit[i] == 0)
        {
            k = i;
            break;
        }
    }
    return k;
}

int main()
{
    cout << "请输入数组行列数：" << endl;
    int x, y;
    cin >> x >> y;
    A shu;
    set(shu, x, y);
    ofstream fout("D:\input.txt",ios::binary);
    for (int i = 1; i <= shu.dianx; i++)
    {
        fout << shu.dian[i] ;
        if (shu.xian[i][i + 1] == 1)
            fout << "   ";
        else
            fout << " ";
    }
    long long int v = 1, b[N] = { 0 }, h = 0;
    for (int i = 1; i <= shu.dianx; i++)
    {
        if (shu.dian[i]<0)
        {
            b[i] = shu.dian[i];
        }
        else
        {
            long long int visit[N] = { 0 };
            long long int max = 0;
            bianli(shu, i, visit, b[i], max, x);
        }
    }

    long long int max = b[1];
    for (int i = 2; i <= shu.dianx; i++)
    {
        if (b[i]>max)
            max = b[i];
    }
    fout << "最大联通子数组的和为：" << max << endl;
}

结果截图：

本次编程中出现了一个困扰了很久的小问题，在文件中输出不能换行，后上网得知把endl改为 即可。