Dreamoon loves summing up something for no reason. One day he obtains two integers a and b occasionally. He wants to calculate the sum of all nice integers. Positive integer x is called nice if 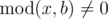 and
and 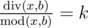 , where k is some integer number in range[1, a].
, where k is some integer number in range[1, a].
By 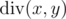 we denote the quotient of integer division of x and y. By
we denote the quotient of integer division of x and y. By 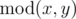 we denote the remainder of integer division of x andy. You can read more about these operations here: http://goo.gl/AcsXhT.
we denote the remainder of integer division of x andy. You can read more about these operations here: http://goo.gl/AcsXhT.
The answer may be large, so please print its remainder modulo 1 000 000 007 (109 + 7). Can you compute it faster than Dreamoon?
The single line of the input contains two integers a, b (1 ≤ a, b ≤ 107).
Print a single integer representing the answer modulo 1 000 000 007 (109 + 7).
1 1
0
For the first sample, there are no nice integers because 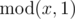 is always zero.
is always zero.
For the second sample, the set of nice integers is {3, 5}.
题意:给你a,b,现在对所有x满足 div(x,b)/mod(x,b) =k (1<=k<=a) 的x求和 取摸.
题解: 设y=div(x,b),z=mod(x,b),
可以得到
y=z*k,y*b+z=x,联立得
(kb+1)z=x,
下面用到求和公式,
然后假设k为常量,得到x=b(b-1)*(kb+1)/2,
最后k还原为变量,得到x=b(b-1)/2*[(1+a)a*b/2+a]


///1085422276 #include<bits/stdc++.h> using namespace std ; typedef long long ll; #define mem(a) memset(a,0,sizeof(a)) inline ll read() { ll x=0,f=1; char ch=getchar(); while(ch<'0'||ch>'9') { if(ch=='-')f=-1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=x*10+ch-'0'; ch=getchar(); } return x*f; } //**************************************** ll mod =1000000007; #define maxn 100000+5 ll a,b; int main(){ a=read(),b=read(); a=((b*((a*(a+1)/2)%mod))%mod+a)%mod;b=((b*(b-1))/2)%mod; cout<<(a*b)%mod<<endl; return 0; }