二维数组最大子数组的和

1.输入一个二维整形数组，数组里有正数也有负数。
2.二维数组中连续的一个子矩阵组成一个子数组，每个子数组都有一个和。
3.求所有子数组的和的最大值。要求时间复杂度为O(n)。

结对编程要求：
两人结对完成编程任务。
一人主要负责程序分析，代码编程。
一人负责代码复审和代码测试计划。
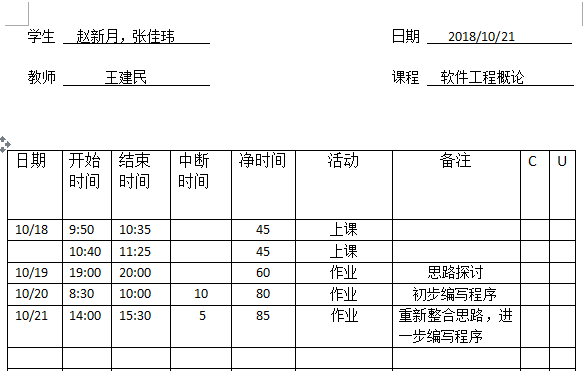
发表一篇博客文章讲述两人合作中的过程、体会以及如何解决冲突(附结对开发的工作照)

 设计思想：任意输入一个数组，有正有负，以第0行第0列元素为起点，分别计算i=1时矩阵和，i=2时矩阵和（j=0,1,2....），i=3（j=0,1,2....）时矩阵和等以此类推。

 创作过程：由于我们只有思想，但是由于个人基础问题不好实现，所以找到了信息院同学帮我们先在网上找到类似代码理一下思路，之后再按照类似思路初步编写，在专业同学的帮助下总算是完成了。

代码：

#include <iostream>
using namespace std;
#define M 1000
int A[M][M];
int AS[M][M];
inline int ArraySum(int s, int t, int i, int j)//定义求数组部分和函数
{
    return AS[i][j] - AS[i][t - 1] - AS[s - 1][j] + AS[s - 1][t - 1];
}
int max(int a, int b)
{
    return(a>b ? a : b);
}
int main()
{
    int m, n, i, j;
    cout << "请输入数组的行:";
    cin >> n;
    cout << "请输入数组的列:";
    cin >> m;
    cout << "请输入一个数组:" << endl;
    for (i = 0; i<n; i++)
    {
        for (j = 0; j<m; j++)
        {
            cin >> A[i][j];
        }
    }
    // 计算数组的部分和  
    for (i = 0; i<n; i++)//以(0,0)为定点一直到(i,j)求部分和
    {
        for (j = 0; j<m; j++)
        {
            AS[i][j] = A[i][j] + AS[i - 1][j] + AS[i][j - 1] - AS[i - 1][j - 1];
        }
    }
    int Max = A[0][0];
    for (int a = 0; a<n; a++)
    {
        for (int c = a; c<n; c++)
        {
            // 将子数组上下边界设为第a行和第c行，在这些子数组中取最大值  
            int IV = ArraySum(a, 0, c, 0);
            for (j = 1; j<m; j++)
            {
                IV = max(ArraySum(a, j, c, j), ArraySum(a, j, c, j) + IV);
                Max = max(IV, Max);
            }
        }
    }
    cout << "数组最大子数组之和为:" << Max << endl;
}

 实现效果：

 

 

 

 

照片：

 组员：赵新月https://www.cnblogs.com/xinyue6/