10、红黑树

一、红黑树的特性:

　　（1）每个节点或者是黑色，或者是红色。
　　（2）根节点是黑色。
　　（3）每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！]
　　（4）如果一个节点是红色的，则它的子节点必须是黑色的。
　　（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

注意：
　　(01) 特性(3)中的叶子节点，是只为空(NIL或null)的节点。
　　(02) 特性(5)，确保没有一条路径会比其他路径长出俩倍。因而，红黑树是相对是接近平衡的二叉树。

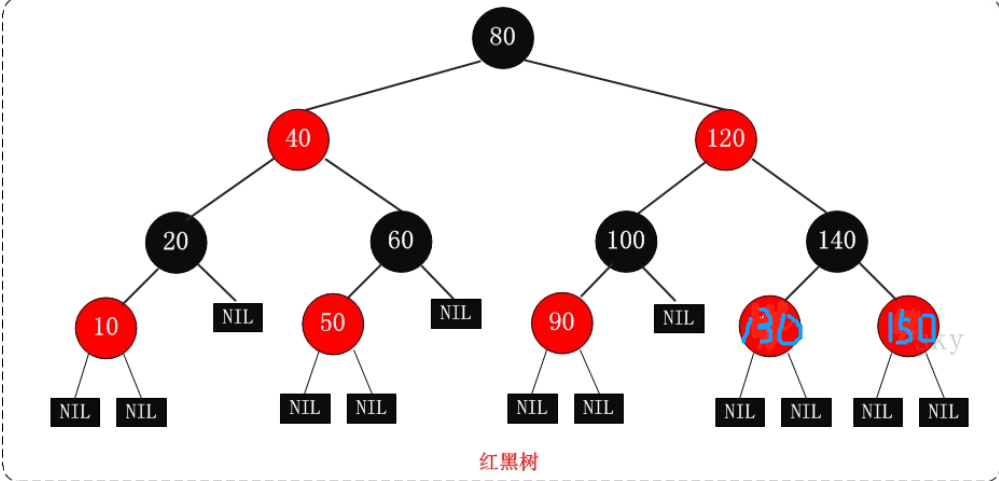
红黑树示意图如下：

　　　　　　　　　　　　　　

二、红黑树的应用:

　　红黑树的应用比较广泛，主要是用它来存储有序的数据，它的时间复杂度是O(lgn)，效率非常之高。

　　（1）C++ STL中的set、map。

　　（2）Linux虚拟内存的管理（linux中进程的调度）。

三、红黑树的基本操作（一）： 单左旋、单右旋和双旋转

　　红黑树的基本操作是添加、删除。在对红黑树进行添加或删除之后，都会用到旋转方法。为什么呢？道理很简单，添加或删除红黑树中的节点之后，红黑树就发生了变化，可能不满足红黑树的5条性质，也就不再是一颗红黑树了，而是一颗普通的树。而通过旋转，可以使这颗树重新成为红黑树。简单点说，旋转的目的是让树保持红黑树的特性。
旋转包括两种：左旋 和 右旋。下面分别对它们进行介绍。

　　1. 左旋

　　　　

 　　对照上面这张图，以x为中心，左旋的代码如下：

//T：红黑树，   x：要以x为中心去左旋
void rbree_left_rotate(rbtree *T,rbtree_node *x)
{
    if (x == T->nil) return;

    //左旋就是改变6个指针的指向，

    //改变第一对指针的指向
    rbtree_node *y = x->right;
    x->right = y->left;
    if (y->left != T->nil)
        y->left->parent = x;
    

    //改变第二对指针的指向
    y->parent = x->parent;
    if (x->parent == T->nil)
        T->root = y;
    else if (x == x->parent->left)
        x->parent->left = y;
    else
        x->parent->right = y;

    //改变第三对指针的指向
    y->left = x;
    x->parent = y;
}

 　　2. 右旋

　　右旋的话，只要将上面的左旋代码中，x和y、left和right相互替换就可以了。以y为中心，右旋的代码如下：

　　　　

//右旋   T：红黑树，   y：要以y为中心去右旋
void rbree_right_rotate(rbtree *T, rbtree_node *y)
{
    if (y == T->nil) return;

    //左旋就是改变6个指针的指向，

    //改变第一对指针的指向
    rbtree_node *x = y->left;
    y->left = x->right;
    if (x->right != T->nil)
        x->right->parent = y;


    //改变第二对指针的指向
    x->parent = y->parent;
    if (y->parent == T->nil)
        T->root = x;
    else if (y == y->parent->right)
        y->parent->right = x;
    else
        y->parent->left = x;

    //改变第三对指针的指向
    x->right = y;
    y->parent = x;
}

　　3.双旋转

　　　　暂不介绍

四、红黑树的基本操作(二) ：添加

 　　插入节点是应注意：插入之前，此树的结构就是红黑树，并满足红黑树的5个性质，当插入黑色的节点为黑色，容易改变黑色的高度，所以要插入的节点为红色共容易满足红黑树的5个性质。但不是所有插入红色都可以满足，所以需要我们调整。以下为需要调整的情况:

当前节点是红色的，父节点也是红色的，此时这种条件下分为2种情况：

　　（1）父节点为祖父节点的左节点时：

　　　　　1）叔父节点为红色时：此时这种情况最简单，只需要将父节点颜色改为黑色，叔父的节点改为黑色，祖父的节点改为红色。

　　　　　2）叔父节点为黑色时：如果插入的这个节点为父节点的右节点，则需要本节点指向父节点，然后绕着父节点左旋。　

　　（2）

　　　　　1）叔父节点为红色时：此时这种情况最简单，只需要将父节点颜色改为黑色，叔父的节点改为黑色，祖父的节点改为红色。

　　　　　2）叔父节点为黑色时：如果插入的这个节点为父节点的右节点，则需要本节点指向父节点，然后绕着父节点左旋。　

　　

以下举例：

如下图这种情况为：前节点是红色的，父节点也是红色的、父节点为祖父节点的左节点、并且叔父节点为红色时，需要做的操作

 

五、各个操作的总代码：

#include "stdafx.h"
#include<windows.h>
#include<assert.h>

#define RED                1
#define BLACK             2

typedef int KEY_TYPE;


typedef struct _rbtree_node
{
    unsigned char color;
    struct _rbtree_node *right;
    struct _rbtree_node *left;
    struct _rbtree_node *parent;
    KEY_TYPE key;
    void *value;
}rbtree_node;

typedef struct _rbtree
{
    rbtree_node *root;
    rbtree_node *nil;
}rbtree;


//左旋   T：红黑树，   x：要以x为中心去左旋
void rbtree_left_rotate(rbtree *T, rbtree_node *x)
{
    if (x == T->nil) return;

    //左旋就是改变6个指针的指向，

    //改变第一对指针的指向
    rbtree_node *y = x->right;
    x->right = y->left;
    if (y->left != T->nil)
        y->left->parent = x;
    

    //改变第二对指针的指向
    y->parent = x->parent;
    if (x->parent == T->nil)
        T->root = y;
    else if (x == x->parent->left)
        x->parent->left = y;
    else
        x->parent->right = y;

    //改变第三对指针的指向
    y->left = x;
    x->parent = y;
}

//右旋   T：红黑树，   y：要以y为中心去右旋
void rbtree_right_rotate(rbtree *T, rbtree_node *y)
{
    if (y == T->nil) return;

    //左旋就是改变6个指针的指向，

    //改变第一对指针的指向
    rbtree_node *x = y->left;
    y->left = x->right;
    if (x->right != T->nil)
        x->right->parent = y;


    //改变第二对指针的指向
    x->parent = y->parent;
    if (y->parent == T->nil)
        T->root = x;
    else if (y == y->parent->right)
        y->parent->right = x;
    else
        y->parent->left = x;

    //改变第三对指针的指向
    x->right = y;
    y->parent = x;
}

//调整
void rbtree_insert_fixup(rbtree *T, rbtree_node *z) 
{
    while (z->parent->color == RED) 
    { //z ---> RED
        if (z->parent == z->parent->parent->left) 
        {
            rbtree_node *y = z->parent->parent->right;
            if (y->color == RED) 
            {
                z->parent->color = BLACK;
                y->color = BLACK;
                z->parent->parent->color = RED;

                z = z->parent->parent; //z --> RED
            }
            else 
            {
                if (z == z->parent->right) 
                {
                    z = z->parent;
                    rbtree_left_rotate(T, z);
                }

                z->parent->color = BLACK;
                z->parent->parent->color = RED;
                rbtree_right_rotate(T, z->parent->parent);
            }
        }
        else 
        {
            rbtree_node *y = z->parent->parent->left;
            if (y->color == RED) {
                z->parent->color = BLACK;
                y->color = BLACK;
                z->parent->parent->color = RED;

                z = z->parent->parent; //z --> RED
            }
            else 
            {
                if (z == z->parent->left) 
                {
                    z = z->parent;
                    rbtree_right_rotate(T, z);
                }

                z->parent->color = BLACK;
                z->parent->parent->color = RED;
                rbtree_left_rotate(T, z->parent->parent);
            }
        }
    }

    T->root->color = BLACK;
}

//插入
void rbtree_insert(rbtree *T, rbtree_node *z) 
{
    //此时插入的代码和二叉排序树的插入相似
    rbtree_node *y = T->nil;
    rbtree_node *x = T->root;

    while (x != T->nil) {
        y = x;
        if (z->key < x->key) {
            x = x->left;
        }
        else if (z->key > x->key) {
            x = x->right;
        }
        else { //Exist
            return;
        }
    }

    z->parent = y;
    if (y == T->nil) {
        T->root = z;
    }
    else if (z->key < y->key) {
        y->left = z;
    }
    else {
        y->right = z;
    }

    z->left = T->nil;
    z->right = T->nil;
    z->color = RED;

    //插入后不符合5个性质，则调整
    rbtree_insert_fixup(T, z);
}

int _tmain(int argc, _TCHAR* argv[])
{
    

    system("pause");
    return 0;
}