《编程珠玑》读书笔记2

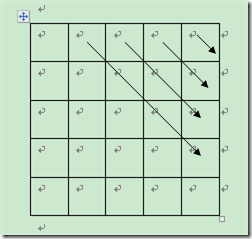
实战演练：动态规划矩阵连乘最优组合

麻烦来了，今天晚上在实现“动态规划矩阵连乘最优组合”的算法在这个问题中需要填表，通过动态规划解体，就因为表的下标混乱，所以填表的过程比较枯燥（debug了好多次）。 我先在稿纸上用伪代码大概解决了这个问题，但是在真正敲写代码的时候，却发现“伪代码”除了整体上的走向之外（大概的结构），很多细节都有问题。

“大概”伪代码：

for i=[0,n-1) 
    for j=[0,n-1-i) 
        col =...    //col是填表元素的列 
        min =... 
        for k=[0,i) 
            t =.... 
            if t<min 
                t = min 
        a[j][col] = min;

其中省略号内的东西待敲进去之后都不正确！需要重新分析这个填表的过程。

捣乱的分析过程

顺序填表分成n-1组，编号i=[0,n-2]，如图：

而每组有j=n-1-i个元素需要填写。于是伪代码的前两行是这样的来的

for i=[0,n-1) 
    for j=[0,n-1-i)

首先把当下需要填写元素的列值得出是col = i+j+1;通过观察很容易发现的；而j即为当下需要填写元素的行，于是(j,col)就是需要填写元素的位置。 

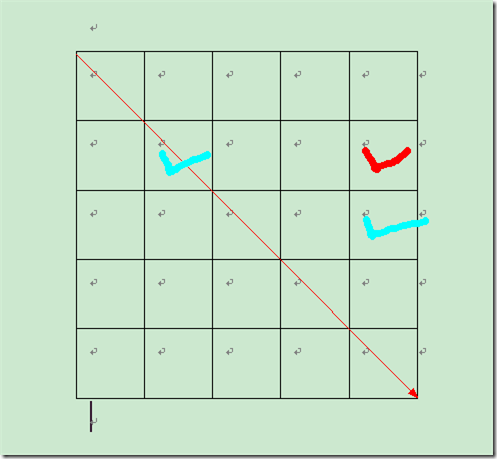
而min的计算是瓶颈，画图

可以发现计算min的两个辅助元素的（第一个元素）行和（第二个元素）列都不被当下需填写元素的(j,col)决定了。于是：

min = a[j][j] + a[j+1][col] + tab[j]*tab[j+1]*tab[col];
接下来的t的计算由上面的min的计算的出来的：      
t = a[j][j+k+1] + a[j+k+2][col] + tab[j] * tab[j+k+2] * tab[col+1];
其实是一样的，只不过红色部分多加了个k+1。

分析过程不够严谨细腻，但是纵观下来，自己有一个清晰的思路。

void optimal_matrix(int * tab,int n) 
{ 
    assert(n!=0);
    int ** a = new int *[n];
    for(int i=0; i<n; i++) 
        a[i] = new int[n], 
        ::memset(a[i],0,sizeof(int)*n);
    int i,j,t,min,col; 
    for(i=0; i<n; i++) 
        a[i][i] = 0;
    for(i=0; i<n-1; i++)//组计数器 
    { 
        for(j=0; j<n-1-i; j++)//每组个数计数器 
        { 
             col = i + j + 1; 
             assert(col+1<n+1); 
             min = a[j][j] + a[j+1][col] + tab[j] * tab[j+1] * tab[col+1];
             for(int k=0; k<i; k++) 
             { 
                 assert(j+k+2<n); 
                 t = a[j][j+k+1] + a[j+k+2][col] + tab[j] * tab[j+k+2] * tab[col+1]; 
                 if(t<min) min = t; 
             }// for 
             a[j][col] = min; 
        }// for 
    }// for 
    cout << a[0][n-1] << endl; 
    delete [] a; 

要做到上面的条条框框实在是不容易的，但是如果养成“条条框框”的习惯的话，即使没有稿纸，只操手MSPAINT，相信敲代码的效率会提高的。

断言的魅力 

“脚手架”简单来说是“验证程序”的程序，但笔者认为“断言”的魅力更大些。在每一个程序中，有一些变量数据是至关重要的，经常Debug就是为了这些变量的检测，看是否和预期中的结果一样；如果不一样我的做法就是：结束debug，开始艰苦的错误排查，这个过程非常头疼。assert能够可以扫清很多的错误细节，包括除数为0，数据超出规定的范围，数组下标越界云云。所以添加断言，能在逻辑上保证你的程序不会出错，即使现实并非如此。

故在上面“动态规划矩阵连乘最优组合”中，添加了

assert(n!=0); 
assert(col+1<n+1); 
assert(j+k+2<n); 

来保证数组下标越界问题，很明显，如果下标越界，将是毁灭性的bug。

另外，添加了一个show函数：

void show(int ** a,int n) 
{ 
    for(int i=0; i<n; i++) 
    { 
        for(int j=0; j<n; j++) 
        cout << setw(6) <<a[i][j]; 
        cout << endl; 
    }// for 
    cout << endl; 
}

这是验证程序的一部分，另外关于程序运行时间外链一篇文章，里面的方法不错，不仅可以精确到ms，还可以是us。

一个算法题

第八章提出了找出一个数字序列中最大的、连续的子序列，并且规定全负子序列的和为0。

“如果没有阅读过《编程珠玑》跳到第四点。”

1. 最原始穷举的算法时间开销大到O(n^3)； 
2. 另一种穷举的算法，即平方算法。通过保存中间结果或者预处理数据，省去了之后重复的计算，是备忘录算法（简单的动态规划），开销下降了一个数量级O(n^2)； 
3. 分治法，这个真没想到，开销再次下降O(nlogn)； 
4. 以前做过类似的题目，所以最先想到的就是这个方法。形象点就是，“边吃边拉”——扫描算法，运行时间为O(n)。 

for i=[0,n) 
    t += a[i] 
    if t<max case 
        max = t 
    if t<0 case 
        t = 0 
end.

课后习题第10题，“找到总和最接近0的子序列或者最接近某个数的子序列”，尝试着用上面的“边吃边拉”算法解决，但是没有成功；只能按着上面说的平方算法，伪代码如下：

nearest = INF 
for i=[0,n) 
    for j=[i,n) 
        t = tab[j] - tab[i] 
        if nearest>|t| case 
            nearest = t 
end

数组用负数索引

第八章最有趣的地方就是“数组索引下标居然可以出现复数”！写了将近两年的程序居然还不知道有这个东西，略有自惭形秽的味道。
设原数组a[n],pa = &a[1]，那么pa[-1]亦即a[0]。但是，这么巧妙的东西，该怎么用？ 大家一开始都有写过“冒泡排序”，看看利用这个“巧妙”能有什么效果？给出伪代码：

bubble(a,n) 
    mustbe(n>1) 
    pa = &a[1] 
    for i=[0,n) 
        for j=[0,n-i) 
            if a[j]>pa[j] case 
                swap(a[j],pa[j]) 
end

是的，它既没有改善冒泡的运行开销和效率，但是代码美观了很多：通过把pa定位在a的第二个元素上，所以a[j]和pa[j]其实不是同一个元素，pa[j]在a[j]的后面，即便他们的下标相同。笔者突然想到了一个比较现实而有用例子，大家一开始学习编程的时候，几乎都遇到过这样的题目，给定一个数字数组，求数组的各元素的总和，最原始的想法：

sum(a,n) 
    for i=[0,n) 
        sum += a[i]; 
end

看看结合上面的“巧妙”的伪代码：

sum(a,n) 
    pa = &a[n-1] 
    t = n>1; 
    for i=[0,t) 
        sum += (a[i]+pa[i|0x8000])    //下标变为负数 
    if n&1 case 
        sum += a[t] 
end

没错，他还是做了n次的加法，一次都没减，但是也有小小的优化：for循环里对i的判断判断和自增都减半！加减开销比位运算大的。“啊哈，灵机一动！”。非常文艺青年的一个优化，非常诗意...