参考自 http://deeplearning.stanford.edu/wiki/index.php/%E5%8F%8D%E5%90%91%E4%BC%A0%E5%AF%BC%E7%AE%97%E6%B3%95
神经网络的代价函数
假设我们有一个固定样本集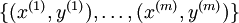 。当使用批量梯度下降法求解时,单个样例的代价函数为:
。当使用批量梯度下降法求解时,单个样例的代价函数为:
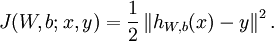
这是个方差代价函数,对于整体的代价函数则为:
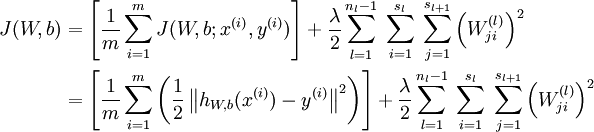
后面的项为规则化项,目的是防止过拟合
我们的目标是针对参数W,和b(其实可以设定一个x0=1以及W0来把b规避掉)来求其函数J(W,b)的最小值。这里的处理方式与普通的线性回归和逻辑回归不同,参数的初始化不能再简单的全部置0,而是使用随机值,比如使用正态分布 Normal(0,ε2)生成的随机值,ε取0.01,然后再使用梯度下降法。否则会法制最后所有隐藏单元最终会得到与输入值有关的、相同的函数
使用梯度下降法中每一次迭代都按照如下公式对参数W和b进行更新:
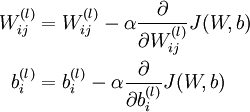 α是学习速率
α是学习速率
其关键在于计算偏导数,这里有一种有效的方法,就是后向传播算法(BP)
后向传播算法
后向传播的实质是在求各层的损失函数的导函数时,由于每一层的输入是前一层的输出的线性组合,所以该层的导函数一定与前一层的损失函数的导数相关相关
具体来说,各层的代价函数的导函数如下:
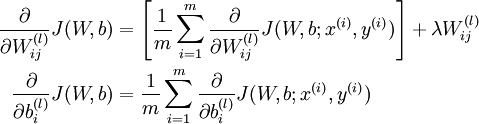
下面少一项是因为规则项不作用于常数项上
反向传播的具体执行思路为,
1)先进行前导计算,算出直到最后一层(输出层)的激活值(输出值)
2)最后一层的每个输出单元i,根据以下公式计算残差:
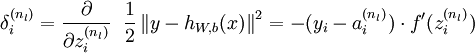
(其实和普通的线性回归没差)
3)对于l = nl-1,nl-2,nl-3...的各层,第l层的第i个节点的残差计算方法如下:
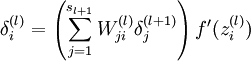
推导公式如下(以nl和nl-1层为例,其他的类推即可)
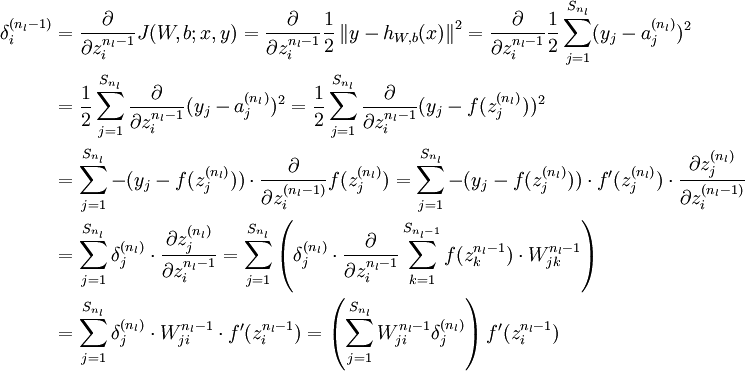
4)计算我们需要的偏导数,方法为:

以上步骤写作向量形式为:
1)前向计算
2)对于输出层
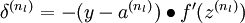 中间的大黑点表示matlab中.*的运算
中间的大黑点表示matlab中.*的运算
3)对于输出层前面的各层
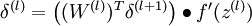
4)计算最终需要的偏导数值:
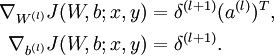
若f(z)是sigmoid的函数,且我们在前向计算中已经算到了 。我们可以利用前面的结论得到
。我们可以利用前面的结论得到
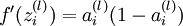
最后整个算法可以表示如下:
1)对于所有l,有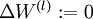 ,
,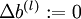 (设为全零向量或全零矩阵)这是为了存储所有的损失函数导函数
(设为全零向量或全零矩阵)这是为了存储所有的损失函数导函数
2)对于i = 1 to m(所有训练样本)
a.使用反向传播算法计算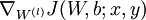 和
和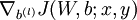
b.计算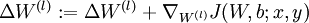
c.计算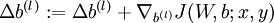
3)更新权重参数:

这只是一次迭代的操作,反复进行该操作,以减小代价函数(损失函数)J,最终求解该神经网络