【数学建模】——模拟退火算法（SAA）

模拟退火算法（SAA）

启发式算法

什么是启发式算法？

• 基于直观或经验而构造的算法
• 是一种技术，在可接受的成本下去寻找最好的解

启发式算法适用于什么场景

• 寻找最优解
• 如何平衡局部搜索与全局搜索；有效逃离局部最优解；

还有哪些启发式算法？

• 群体智能算法便是启发式算法

• 动物

  • 粒子群优化，蚂蚁优化，鱼群算法，蜂群算法等；

• 植物

  • 向光性算法，杂草优化算法，等等；

• 人类

  • 和声搜索算法是较好的算法；

模拟退火算法的基本原理

思想

• 借鉴固体的退火过程，当固体的温蒂较高的时候，内能比较大，固体内的粒子处于快速无序运动状态。温度降低，固体内能减少，粒子逐渐趋于有序，最终固体处于常温状态，内能达到最小，此时粒子最为稳定
• 一开始为算法设定一个较高的值T（模拟温度），算法不稳定，选择当前较差解的概率很大；随着T的减小，算法趋于稳定，选择较差解的概率减小，最后，T降至终止迭代的条件，得到近似最优解。

代码

/*
* J(y)：在状态y时的评价函数值
* Y(i)：表示当前状态
* Y(i+1)：表示新的状态
* r： 用于控制降温的快慢
* T： 系统的温度，系统初始应该要处于一个高温的状态
* T_min ：温度的下限，若温度T达到T_min，则停止搜索
*/
while( T > T_min )
{
　　dE = J( Y(i+1) ) - J( Y(i) ) ;

　　if ( dE >=0 ) //表达移动后得到更优解，则总是接受移动
Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
　　else
　　{
// 函数exp( dE/T )的取值范围是(0,1) ，dE/T越大，则exp( dE/T )也
if ( exp( dE/T ) > random( 0 , 1 ) )
Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
　　}
　　T = r * T ; //降温退火 ，0<r<1 。r越大，降温越慢；r越小，降温越快
　　/*
　　* 若r过大，则搜索到全局最优解的可能会较高，但搜索的过程也就较长。若r过小，则搜索的过程会很快，但最终可能会达到一个局部最优值
　　*/
　　i ++ ;
}

clear all; %清除所有变量
close all; %清图
clc ;      %清屏
D = 10;
Xs = 20;%%函数上限
Xx =-20;%%函数下限
%%%%%%%%%%%%%%%%%%%%冷却表参数%%%%%%%%%%%%%%%%%%%%%%%%%%
L= 200;    %马尔可夫链长度
K = 0.998;  %衰减参数
S = 0.01;   %步长因子，就是每次解变化的大小
T = 100;    % 初始温度
YZ = 1e-8;  %容差
P = 0;      %Metropolis过程接受点

%%%%%%%%%%%%%%%%%随机选点初值设定%%%%%%%%%%%%%%%%%%%5
PreX = rand(D,1)*(Xs-Xx)+Xx;%初始化矩阵D × 1的解
PreBestX = PreX;%用于保存上一个最优的解
PreX = rand(D,1)*(Xs-Xx)+Xx;
BestX = PreX;%用于保存当前最优解
%%%%%%%%%%%%%%%%%每迭代一次退火一次（降温），直到满足迭代条件为止%%%%%%%%%
deta = abs(func1(BestX)-func1(PreBestX));%能量差值，适应度差值
while (deta>YZ) && (T>0.001)
    T = K*T;%%降温
    %%%%%%%%%%%%在当前温度T下迭代次数%%%%%%%%%%%%
    for i = 1:L
        %%%%%%%%%%%%在此点附近随机选择下一点%%%%%%%%%%%%%%%
        %%%%%%%%%%%%根据当前条件产生一个新解%%%%%%%%%%%%%%%%%
        NextX  = PreX + S*(rand(D,1) * (Xs-Xx)+Xx);
        %%%%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%
        %%%%%%%%%%%%%%因为上一行代码是随机产生的数，判断产生的数，是否超过定义域范围，超过则重新产生一个数%%%%%%
        for ii = 1:D
            if NextX(ii) > Xs | NextX(ii) < Xx
                NextX(ii) = PreX(ii) + S* (rand * (Xs-Xx)+Xx);
            end
        end
    %%%%%%%%%%%%%%是否全局最优解%%%%%%%%%%%%%%%%%%%%
    if (func1(BestX) > func1(NextX))
        %%%%%%%%%%%%%%%%%%%%保留上一个最优解%%%%%%%%%%%%%%5
        PreBestX = BestX;
        %%%%%%%%%%%%%%%%%此为新的最优解%%%%%%%%%%%%%%%%%
        BestX  = NextX;
    end
        %%%%%%%%%%%%%%%Metropolis过程%%%%%%%%%%%%%%%%%%%
    if(func1(PreX) - func1(NextX)>0)
        %%%%%%%%%%%%%%接受新解%%%%%%%%%%%%%
        PreX = NextX;
        P = P+1;
    else
        %%%%%%%%%%%%%%%%%%%求状态2接受的概率接受新解%%%%
        %%%%%%%%%%%%%%%%%%%随着越来越接近最优值的时候，接受较差的状态的概率越低%%%%%
        changer = -1 * (func1(NextX)-func1(PreX))/T;
        p1 = exp(changer);
        %%%%%%%%%%%%%%%%%%以一定概率接受较差的解%%%%%%%%%%%%%%%%%
        if p1 >rand
            PreX = NextX;
            P =P+1;
        end
    end
    trace(P+1) = func1(BestX);
    
    end
    deta = abs(func1(BestX) - func1(PreBestX));
end

%最小值的解
BestX
%解的适应度
func1(BestX)
figure
plot(trace(2:end))
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')

%%%%%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%

function result = func1(x)
summ = sum(x.^2);
result = summ;
end

TSP

%% 数据导入
clear all; %清除所有变量
close all; %清图
clc ;      %清屏
C=[
    1304 2312;
    3639 1315;
    4177 2244;
    3712 1399;
    3488 1535;
    3326 1556;
    3238 1229;
    4196 1004;
    4312 790;
    4386 570;
    3007 1970;
    2562 1756;
    2788 1491;
    2381 1676;
    1332 695;
    3715 1678;
    3918 2179;
    4061 2370;
    3780 2212;
    3676 2578;
    4029 2838;
    4263 2931;
    3429 1908;
    3507 2367;
    3394 2643;
    3439 3201;
    2935 3240;
    3140 3550;
    2545 2357;
    2778 2826;
    2370 2975
    ];%31个省会坐标
%% 设置参数
% 初始温度
% 衰减参数
n=size(C,1); %TSP问题的规模，即城市数目
T=100*n;     %初始温度
L=100;       %马尔科夫链的长度
K=0.99;      %衰减参数

%%%城市坐标结构体%%%%%%%
city=struct([]);


for i=1:n
    city(i).x=C(i,1);
    city(i).y=C(i,2);
end

l=1;        %统计迭代次数
len(l)=func5(city,n); %每次迭代后路线的长度

figure(1);

while T>0.001
    %%%%%%%%%%%%%%%多次迭代扰动，温度降低前多次试验%%%%%%%%
    for i=1:L
        %%%%%%%%%%%%%%%计算原路线总距离%%%%%%%%%
        len1=func5(city,n);
        %%%%%%%%%%%%%%%产生随机扰动%%%%%%%%%
        %%%%%%%%%%%%%%%随机置换两个不同的城市的坐标%%%%%%%%%
        p1=floor(1+n*rand);
        p2=floor(1+n*rand);
        while p1==p2
            p1=floor(1+n*rand);
            p2=floor(1+n*rand);
        end
        tmp_city=city;
        %%交换元素
        tmp=tmp_city(p1);
        tmp_city(p1)=tmp_city(p2);
        tmp_city(p2)=tmp;
        %%%%%%%%%%%%%%%计算新路线总距离%%%%%%%%%
        len2=func5(tmp_city,n);
        %%%%%%%%%%%%%%%新老距离的差值，相当于能量%%%%%%%%%
        delta_e=len2-len1;
        %%%%%%%%%%%%%%%新路线好于旧路线，用新路线替代旧路线%%%%%%%%%
        if delta_e<0
            city=tmp_city;
        else
            %%%%%%%%%%%%%%%以一定概率选择是否接受%%%%%%%%%
            if exp(-delta_e/T)>rand()
                city=tmp_city;
            end
        end
    end
    l=l+1;          %迭代次数加1
    

    %%%%%%%%%%%%%%%计算新路线的距离%%%%%%%%%
    len(l)=func5(city,n);
    %%%%%%%%%%%%%%%温度不断下降%%%%%%%%%
    T=T*K;
    for i=1:n-1
        plot([city(i).x,city(i+1).x],[city(i).y,city(i+1).y],'bo-');
        hold on;
    end
    plot([city(n).x,city(1).x],[city(n).y,city(1).y],'ro-');
    
    title(['优化最短距离:',num2str(len(l))]);%%num2str将数字转为字符数组
    hold off;
    pause(0.005);

end

figure(2)
plot(len);
xlabel('迭代次数');
ylabel('目标函数值');
title('适应度进化曲线');

%计算距离的函数
function len=func5(city,n)
len=0;
for i=1:n-1
    len=len+sqrt((city(i).x-city(i+1).x)^2+(city(i).y-city(i+1).y)^2);
end
len=len+sqrt((city(n).x-city(1).x)^2+(city(n).y-city(1).y)^2);
end

模拟退火算法的流程图

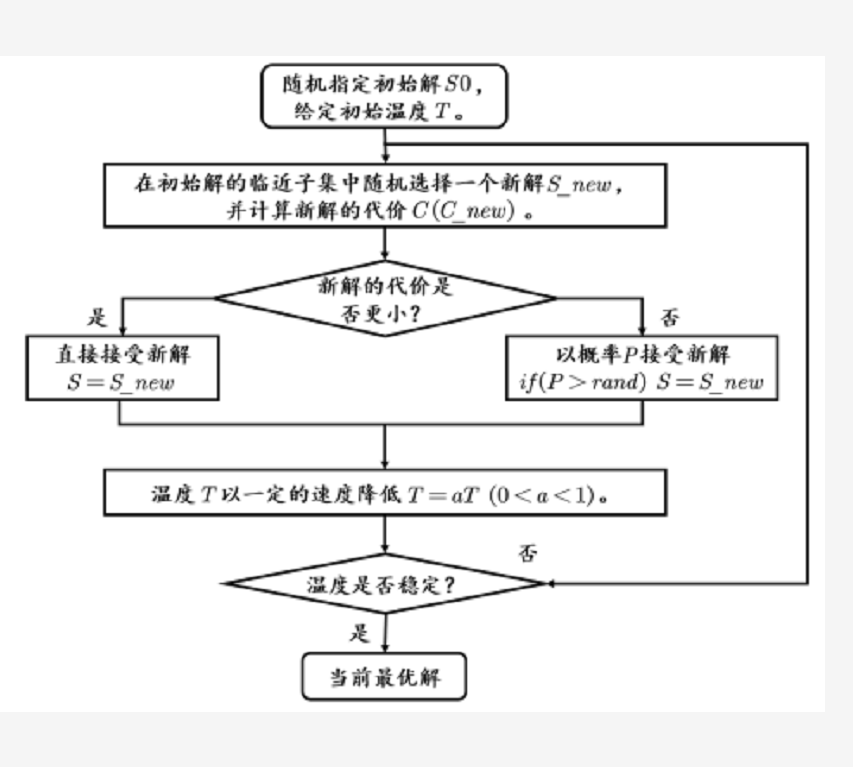
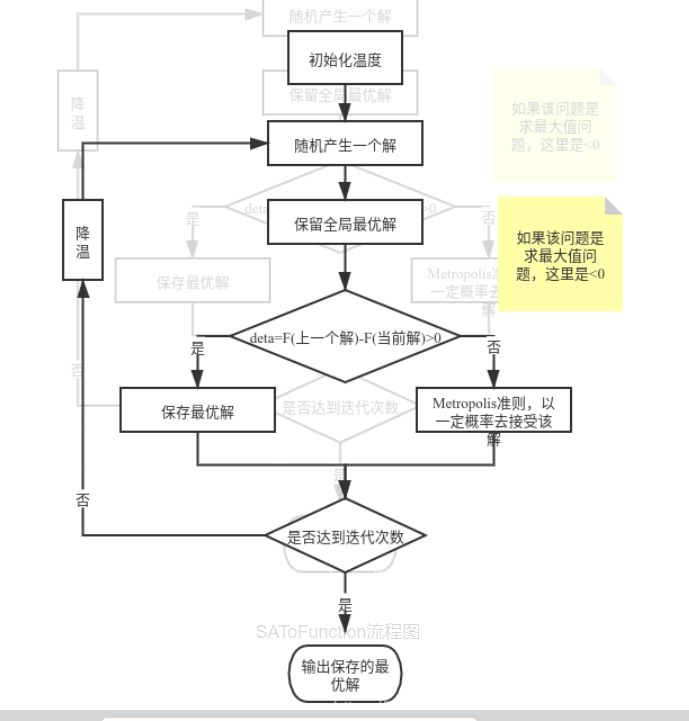
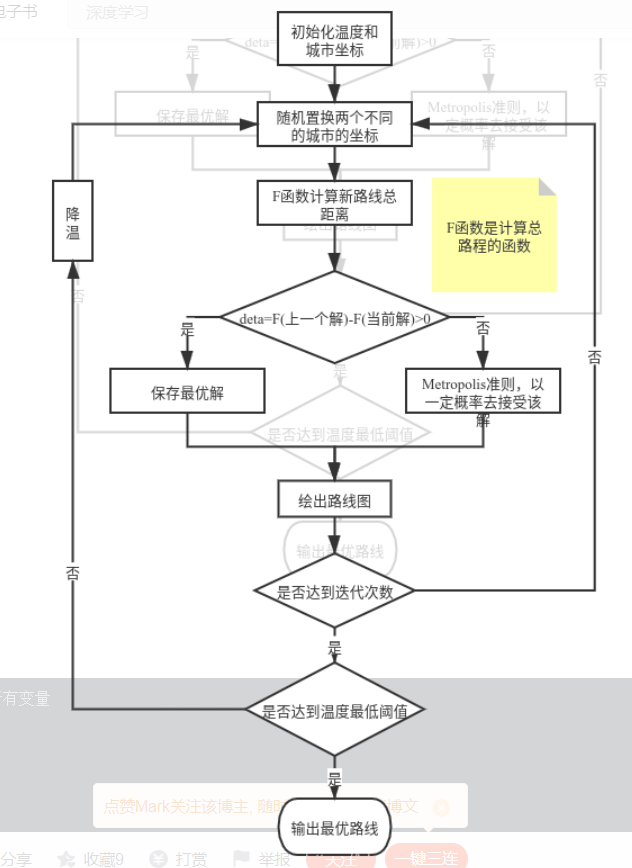
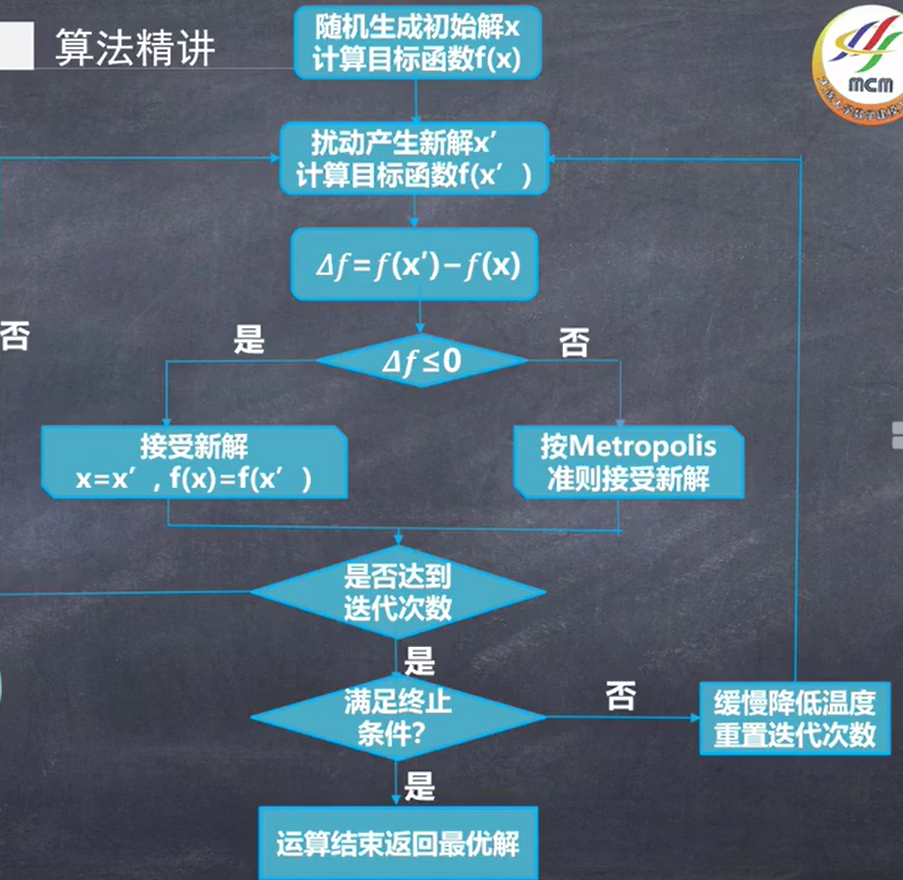
参数讲解

冷却进度表

• 控制温度参数的初值T0

• 控制温度T的衰减函数（温度的更新）

  • 
  • 

• 马尔科夫链的长度Lk（迭代次数）

  • 

• 控制参数T的终值（停止准则）

  • 

Metropolis准则

• 

相似性对比

优缺点

优点

• 高效地解决NP问题（TSP问题和0-1背包问题）
• 相较于其他非线性与优化算法，模拟退火算法编程工作量小且易于实现

缺点

• 使用不当，可能陷入局部最优
• 参数难以控制，所得结果可能为接近最优解但是并非最优解

模拟退火算法的应用

最优化

求解函数最值问题

• 用代码求解
• 用工具箱求解