2021-11-30 14:46:14 星期二
序言
查找,顾名思义,就是从某一集体中找出一个或一种元素。又称检索。
其中,在计算机语言学习中,怎么利用机器对数据进行简便查找更是一项重要的工程。
根据对查找表操作不同,查找又分静态查找和动态查找。
根据查找表的特点,我们可以利用不同的方法进行找到我们所需的那个唯一关键字。
对于静态表的查找方法,这里我们主要介绍
一、顺序查找(线性查找)
二、折半查找(二分或对分查找)
三、静态树表的查找
四、分块查找(索引顺序查找)
对于动态表,我们主要介绍:
典型的动态表—— 二叉排序树
既然有方法了,那么怎么能判断方法的优劣呢?
这样就需要一个工具,来简单的判断该方法的优劣,它就是ASL(平均查找长度)
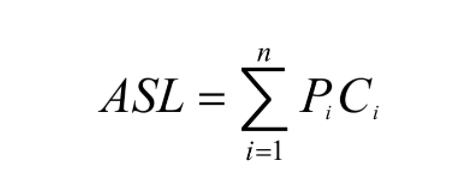
基本概念
查找表:——————由同一类型的数据元素(或记录)构成的集合
查 找:——————查询(Searching)特定元素是否在表中。
查找成功:——————若表中存在特定元素,称查找成功,应输出该记录或位置;
查找不成功:————(与查找成功对立)否则,称查找不成功(也应输出失败标志或失败位置)
静态查找表:————只查找,不改变集合内的数据元素。
动态查找表:——既查找,又改变(增减)集合内的数据元素。
关键字:——记录中某个数据项的值,可用来识别一个记录
主关键字:——可以唯一标识一个记录的关键字
次关键字:——识别若干记录的关键字
工具:ASL
如何评估查找方法的优劣?
明确:查找的过程就是将给定的K值与文件中各记录的关键字项进行比较的过程。所以用比较次数的平均值来评估算法的优劣。称为平均查找长度(ASL:average search length)。
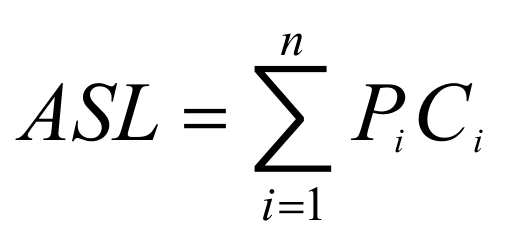
其中:
n是记录个数;
Pi是查找第i个记录的查找概率(通常取等概率,即Pi =1/n);
Ci是找到第i个记录时所经历的比较次数。
物理意义:假设每一元素被查找的概率相同,则查找每一元素所需的比较次数之总和再取平均,即为ASL。
显然,ASL值越小,时间效率越高。
例如:
给定一个集合:1 3 7 4 9 0,顺序查找的方法,查找成功的ASL是多少?
解:对于每一个元素的查找成功的概率相同,都是1/6 既pi = 1/6,然后每个元素被查找成功的比较次数分别为(1,2,3,4,5,6)
ASL = (1+2+3+4+5+6)/6 = 21/6
静态查找表
抽象数据类型的静态查找表的定义为:
ADT StaticSearchTable
{数据对象D:D是具有相同特性的数据元素的集合。每个数据元素均含有类型相同、可唯一标识数据元素的关键字。
数据关系R:数据元素同属一个集合。
基本操作P:
Create(ST,n); 操作结果:构造一个含n个数据元素的静态查找表ST。
Destroy(ST); 操作结果:销毁表ST。
Search(ST,key); 操作结果:若ST中存在其关键字等于key的数据元素,则函数值为该元素的值或者在表中的位置,否则为空。
Traverse(ST,Visit()); 操作结果:按照某种次序对ST的每个元素调用函数VIsit()一次且仅一次,一旦visit()失败,则操作失败
}
(1)顺序表的机内存储结构:
typedef ElemType{
keyType key;
anyType otherItems;
} ElemType
typedef struct {
ElemType *elem; //表基址,0号单元留空。表容量为全部元素
int length; //表长,即表中数据元素个数
}SSTable;
存储图例:
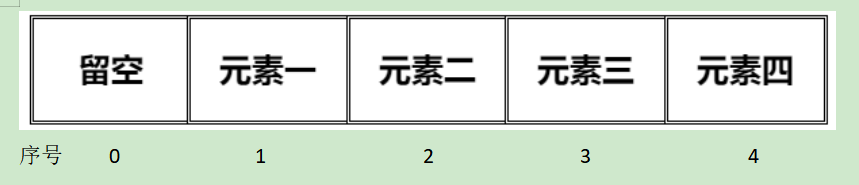
顺序查找
利用上图
如果我们要找出其中的元素四,
首先,要找到其关键字(这里是注关键字)------数组序号也就是长度
然后,选取方法。
这里我们采用第一种方法,也就是顺序查找
Linear search,又称线性查找,即用逐一比较的办法顺序查找关键字,这显然是最直接的办法。
(2)算法的实现:
技巧:把待查关键字key存入表头或表尾(俗称“哨兵”),
若将待查找的key存入顺序表的首部(如0号单元),则顺序查找的实现方案为:从后向前逐个比较!
int Search_Seq( SSTable ST , KeyType key ){
ST.elem[0].key =key; //设立哨兵
for( i=ST.length; ST.elem[ i ].key!=key; - - i );
//从后向前逐个比较
return i;
} // Search_Seq
设立哨兵:可免去查找过程中每一步都要检测是否查找完毕。当n>1000时,查找时间将减少一半。
不要用for(i=n; i>0; - -i) 或 for(i=1; i<=n; i++) 了
到达0号单元(哨兵)结束循环,查找失败,返回0(i=0)。查找成功,则返回该元素位置i。
图例:

等概率下的平均比较查找长度: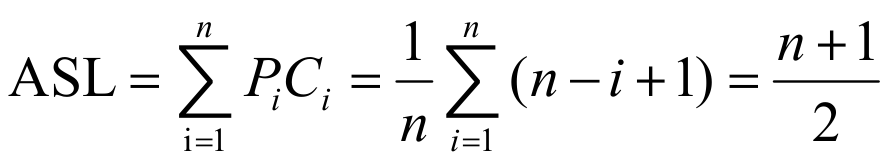

折半查找(二分查找 对分查找)
先给数据排序(例如按升序排好),形成有序表,然后再将key与正中元素相比,若比key小,则缩小至右半部内查找;再取其中值比较,每次缩小1/2的范围,直到查找成功或失败为止。

存储图例:

② 运算步骤:
1)low =1,high =11 ,mid =6 ,待查范围是 [1,11];
2)若 ST.elem[mid].key < key,说明 key[ mid+1,high] ,
则令:low =mid+1;重算 mid= (low+high)/2;.
3)若 ST.elem[mid].key > key,说明key[low ,mid-1],
则令:high =mid–1;重算 mid ;
4)若 ST.elem[ mid ].key = key,说明查找成功,元素序号=mid;
③ 结束条件: (1)查找成功 : ST.elem[mid].key = key
(2)查找不成功 : high≤low (意即区间长度小于0)
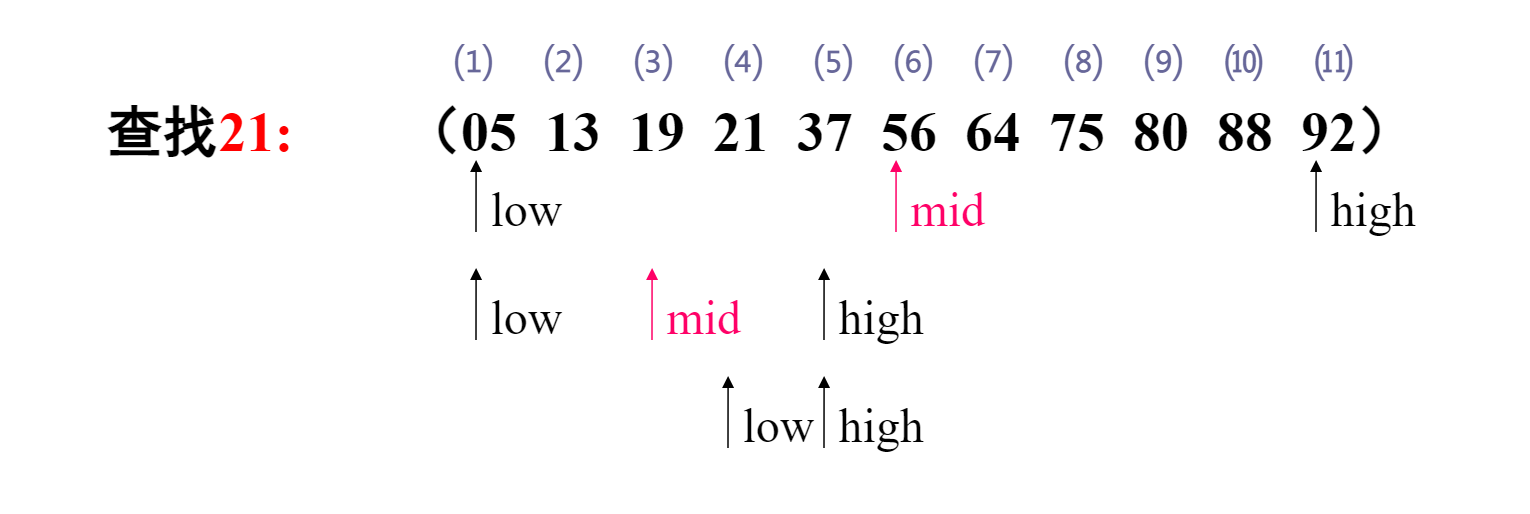
最后(low+high)/2下取整,得mid = 4 得出查找结果:查找成功,21所在位置是4
给出代码
int bin_search(SSTable ST,int key)
{ int low,high,mid;
low=1; high=ST.length;
while(low<=high)
{
mid=(low+high)/2;
if EQ(key,ST.elem[mid].key) return mid; //等于
else if LT(key,ST.elem[mid].key) high=mid-1; //小于
else low=mid+1;
}
return 0;
}/*bin_search*/
算法效率:

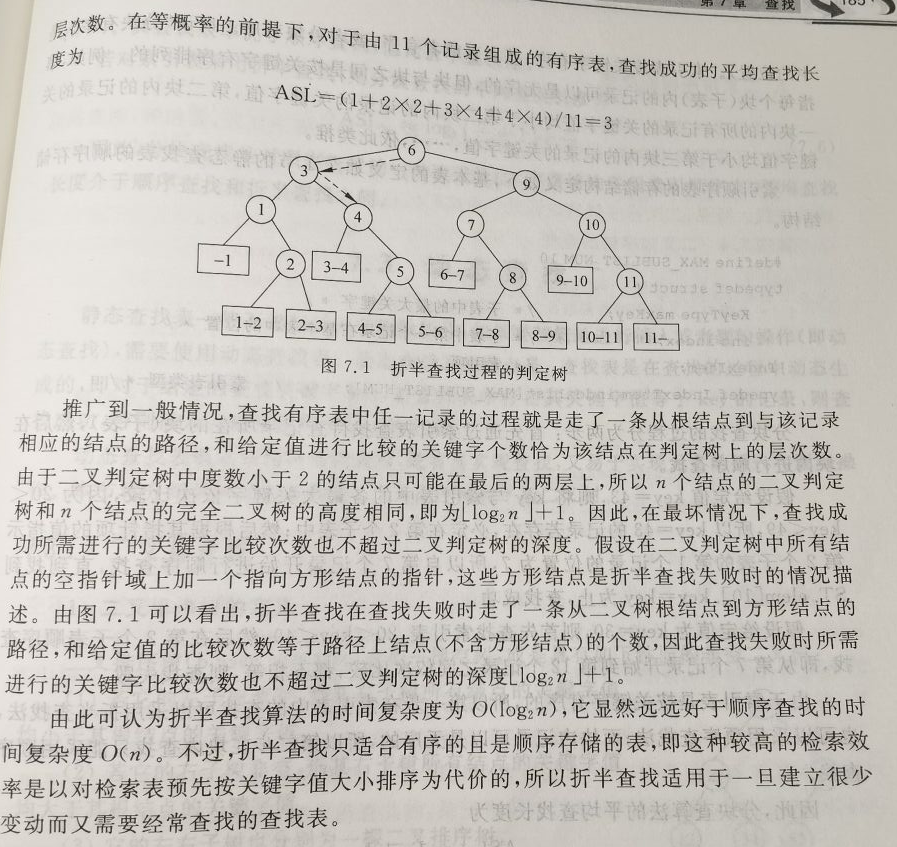
分块查找
又称索引顺序查找这是一种顺序查找的另一种改进方法。
先让数据分块有序,即分成若干子表,要求每个子表中的数值(用关键字更准确)都比后一块中数值小(但子表内部未必有序)。
然后将各子表中的最大关键字构成一个索引表,表中还要包含每个子表的起始地址(即头指针)。
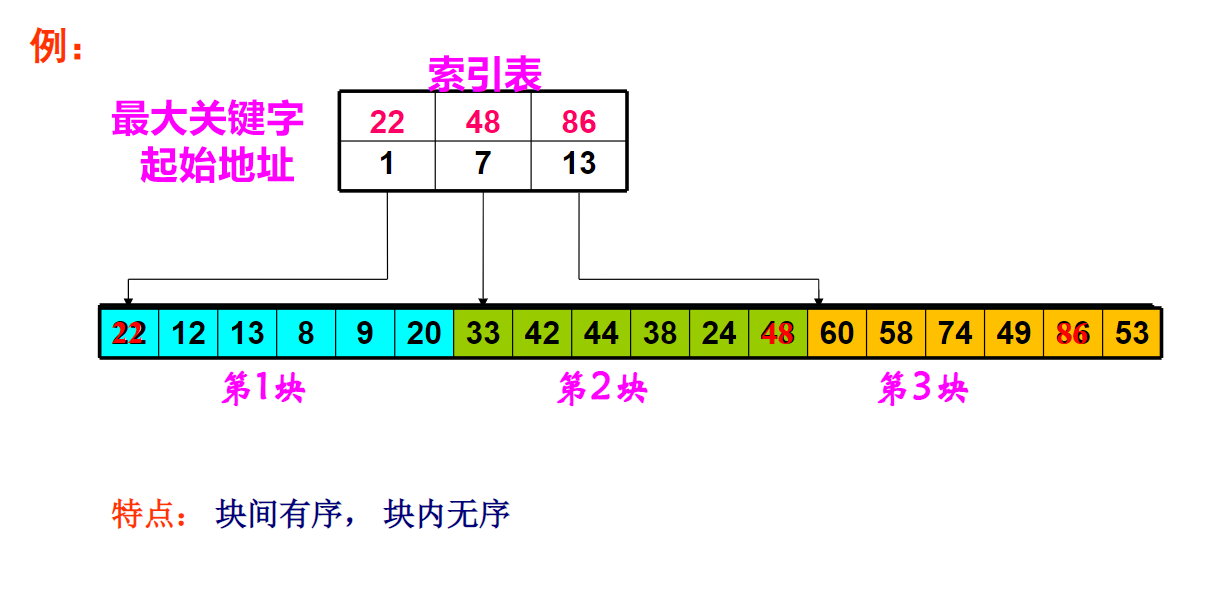
两步走: 首先通过索引表查找待查记录所在的块(子表),然后在块内进行顺序查找
索引表的存储结构定义如下,
#define MAX_SUBLIST_NUM 10
typedef struct{
KeyType maxKey; /*---子表中的最大关键字---*/
int index; /*---子表中第一个记录在基本表中的位置---*/
}IndexItem; /*---索引项---*/
typedef IndexItem indexList[MAX_SUBLIST_NUM]; /*----索引表类型--*/
那么,可以得出分块查找算法的平均查找长度

动态查找表

典型的动态查找表——————二叉排序树
二叉排序树的定义:
或是一棵空树;或者是具有如下性质的非空二叉树:
(1)左子树的所有结点值均小于根的值;
(2)右子树的所有结点值均大于根的值;
(3)它的左右子树也分别为二叉排序树。
从定义上可以看出,二叉排序树是一个可以由递归创建的逻辑结构。
二叉排序的图例:
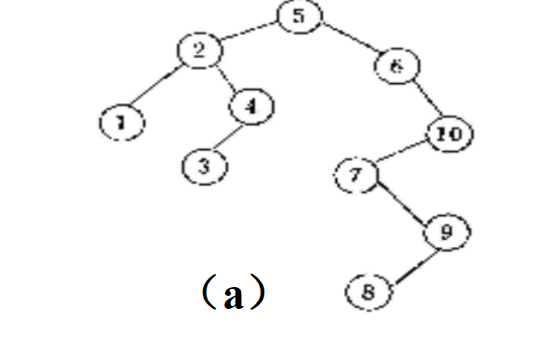
二叉排序树的存储结构(以链表存储为例):
/*---二叉排序树的二叉链表存储结构---*/
typedef struct BTNode{ /*---元素的结点结构---*/
Elemtype key; /*---记录的关键字,忽略记录的其他数据项---*/
struct BTNode *lchild,*rchild; /*---左右指针---*/
}BTNode,*BStree;
二叉排序树的创建,插入,查找,删除
创建与插入
根据定义创建二叉树:
while(序列不为空){
- 顺序拿出元素
- 元素比根结点大,放到根结点的右子树。
- 元素比根结点小,放到根结点的左子树。
- 重复步骤2-3,至成为叶子结点。
}
给出代码:
创建:
BStree CreateBST()
{
BStree T,s;
T = NULL;
printf("输入关键字key,输入“-1”结束。\n");
while(1)
{
scanf("%d",&key); /*---这里假设key是int类型---*/
if(key) break;
s = (BTNode*)malloc(sizeof(BTNode));
s->key = key;
s->lchild = NULL;
s->rchild = NULL;
T = InsertBST(T,s); /*---插入二叉排序树---*/
}
return T;
}
插入(1:递归版本)
BSTree InsertBST(BSTree T,BTNode *s)
{/*---在以T为根的二叉排序树上插入一个指针s所指向的结点的递归算法---*/
if(T==NULL) T = s;
else
{
if(s->key > T->key) T->rchild = InsertBST(T->rchild,s); /*---递归插入到T的右子树中---*/
else if(s->key < T->key) T->lchild = InsertBST(T->lchild,s); /*---递归插入到T的左子树中---*/
}
return T;
}
插入(2:非递归版本)
点击查看代码
BSTree InsertBST(BSTree T,BTNode *s)
{
BSTree p = T;
BTNode *f = NULL;
if(T==NULL)
{
T = s;
return T;
}
while(p)
{
if(p->key == s->key) return T;
f = p; /*---记录访问的结点:便于连接s---*/
if(s->key < p->key)
p = p->lchild;
else p = p->rchild;
}//跳出循环:1.p = null;2.f就是s与之连接的结点
if(s->key > p->key) f->rchild = s;
if(s->key < p->key) f->lchild = s;
return T;
}

查找与删除
查找的基本过程如下:
当二叉树为空时,返回0;
当二叉树不为空时,首先将给定的值key与根结点关键字进行比较,若相等,则查找成功,返回1;否则将依据给定值key与根结点关键字值的大小关系,分别在其左子树或者右子树中继续查找。可见,二叉排序树的查找可以是一个递归的过程。
删除的基本过程:

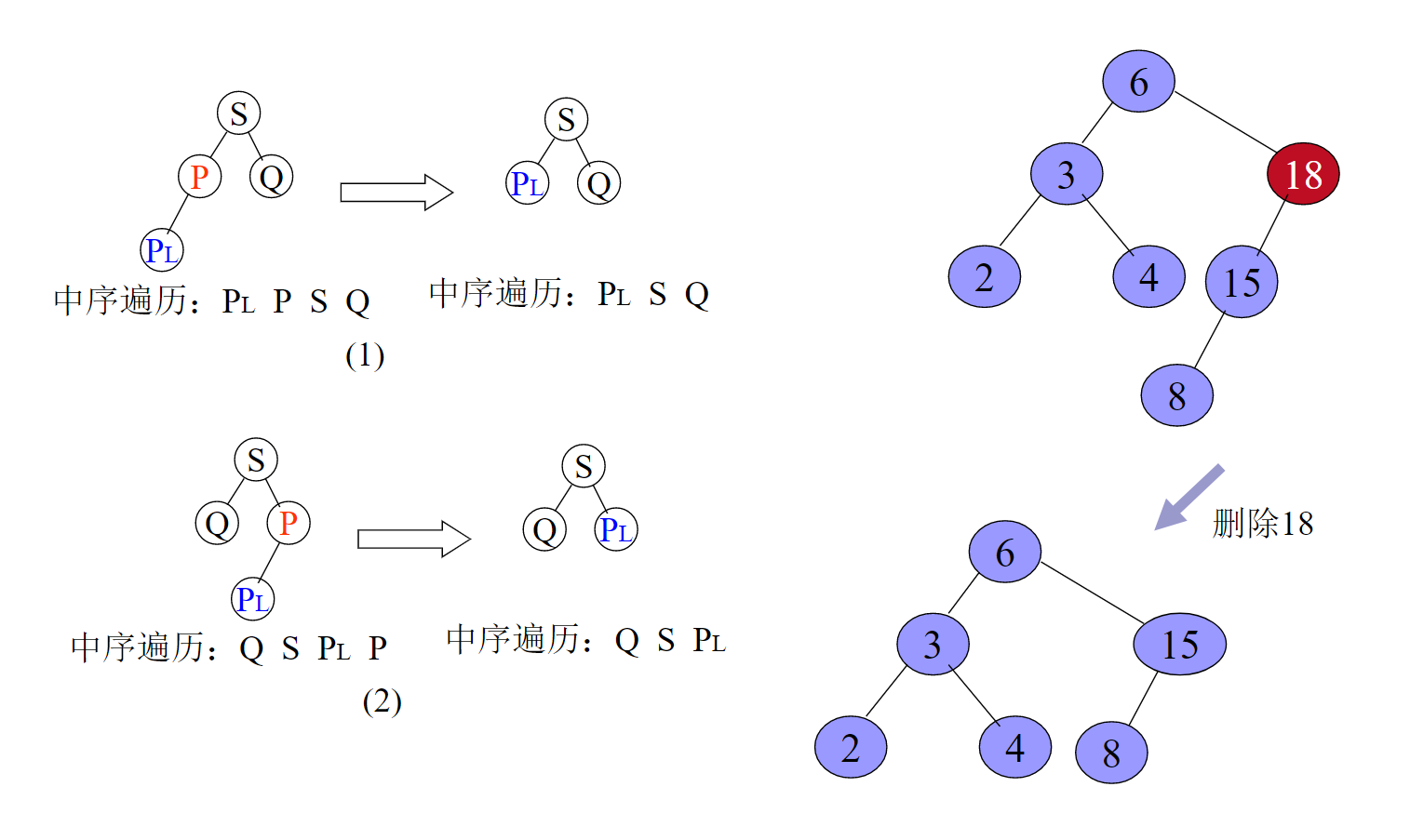
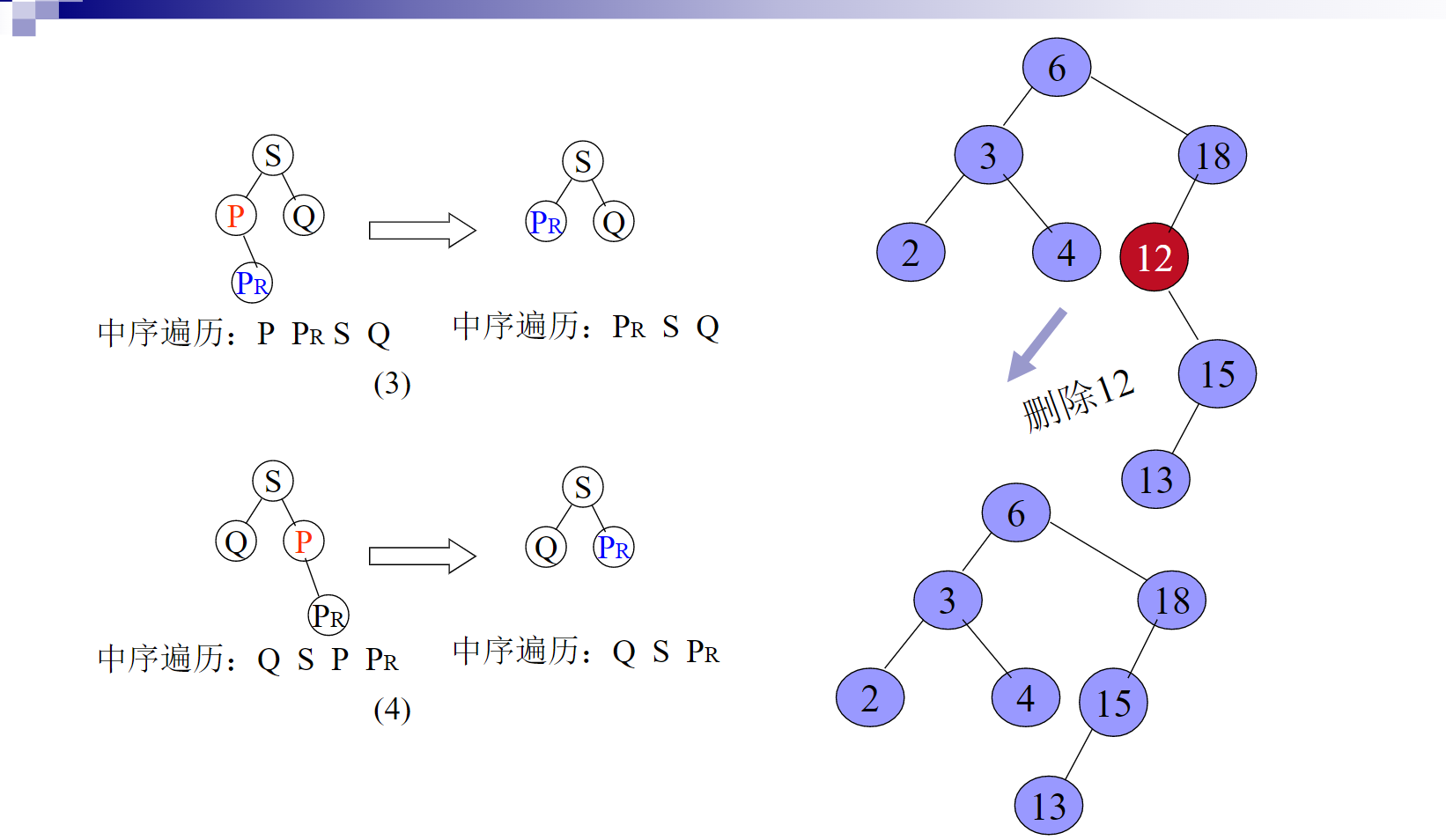
给出代码:
查找代码:
int BSTsearch(BSTree T, int key)
{
BSTree p = T;
if(!p) return 0; /*---空树,返回0---*/
else if(p->key == key) return 1;
else if(p->key > key) BSTsearch(p->lchild,key);
else BSTsearch(p->rchild,key);
}
查找非递归算法
点击查看代码
//二叉排序树查找非递归算法
int BSTsearch2(BSTNode *T, int data)
{
BSTNode *p = T;
while(p)
{
if(p->key == data)
return 1;
p = (p->key > data)? p->lchild : p->rchild;
}
return 0;
}
删除代码:
//二叉排序树删除操作
void DelBST(BSTNode *T,int key)
{
BSTNode *p = T, *f, *q, *s;
while(p)
{
if(p->key == key) break; //找到关键字为key的结点
f=p;//记下关键字key节点的父节点
p=(key < p->key)? p->lchild : p->rchild;//分别在*p的左、右子树中查找
}
if(!p) return;//二叉排序树中无关键字为key的结点
if(p->lchild == NULL && p->rchild == NULL)//p无左子树无右子树
{
if(p == T) T = NULL;//删除的是根节点
else
if(p == f->lchild)
f->lchild = NULL;
else
f->rchild = NULL;
}
else if(p->lchild == NULL && p->rchild != NULL)//p无左子树有右子树
{
if(f->lchild == p)
f->lchild = p->rchild;
else
f->rchild = p->rchild;
}
else if(p->rchild == NULL && p->lchild != NULL)//p有左子树无右子树
{
if (f->lchild == p)
f->lchild = p->lchild;
else
f->rchild = p->lchild;
}
else if(p->lchild != NULL && p->rchild != NULL)//p既有左子树又有右子树
{
q = p;
s = p->lchild;//转左
while(s->rchild)
{//然后向右到尽头
q = s;
s = s->rchild;//s指向被删节点的“前驱”(中序前驱)
}
p->key = s->key;//以p的中序前趋结点s代替p(即把s的数据复制到p中)
if(q != p)
q->rchild = s->lchild;//重接q的右子树
else
q->lchild = s->lchild;//重接q的左子树。
}
}