一、递归的定义
函数的递归调用:是函数嵌套调用的一种特殊形式
具体是指:
在调用一个函数的过程中又直接或者间接地调用到本身
# 直接调用本身 def f1(): print('是我是我还是我') f1() f1()

# 间接接调用本身 def f1(): print('===>f1') f2() def f2(): print('===>f2') f1() f1()

# 一段代码的循环运行的方案有两种 # 方式一:while、for循环 while True: print(1111) print(2222) print(3333) # 方式二:递归的本质就是循环: def f1(): print(1111) print(2222) print(3333) f1() f1()
二、递归的结束
递归调用不应该无限地调用下去,必须在满足某种条件下结束递归调用
n=0 while n < 10: # 设置循环结束条件 print(n) n+=1 def f1(n): if n == 10: # 设置递归结束条件 return print(n) n+=1 f1(n) f1(0)
补充:
''' 1. 可以使用sys.getrecursionlimit()去查看递归深度,默认值为1000,虽然可以使用 sys.setrecursionlimit()去设定该值,但仍受限于主机操作系统栈大小的限制 2. python不是一门函数式编程语言,无法对递归进行尾递归优化。 '''
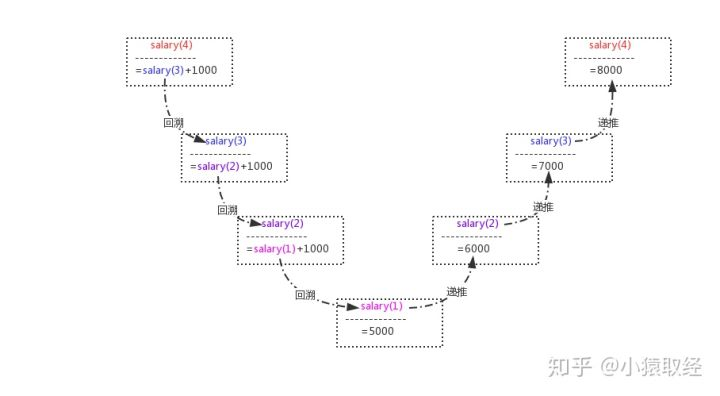
三、递归的两个阶段
回溯:一层一层调用下去
递推:满足某种条件,结束递归,然后一层一层返回
# salry(4) = age(3) + 1000 # salry(3) = age(2) + 1000 # salry(2) = age(1) + 1000 # salry(1) = 5000 def salary(n): if n == 1: return 5000 return age(n-1) + 1000 res=age(4) print(res) # 8000
四、递归应用
4.1 嵌套列表的取值(计算文件夹大小也可这么操作):
l=[1,2,[3,[4,[5,[6,[7,[8,[9,10,11,[12,[13,]]]]]]]]]] def f1(list1): for x in list1: if type(x) is list: # 如果是列表,应该再循环、再判断,即重新运行本身的代码 f1(x) else: print(x) f1(l)
4.2 斐波拉契数列
法一:函数递归得到第n项斐波拉契数列,循环函数得到数列
def print_Fibonacci(n): for i in range(1,n+1): print(Fibonacci(i),end=" ") print() def Fibonacci(n): if n == 1 or n == 2: return n-1 elif n > 2: return Fibonacci(n-2) + Fibonacci(n-1) return -1 print(Fibonacci(15)) print_Fibonacci(15)
法二:设定数列初始的两个值与数列终止值,每次替换初始值为平移一个单位后的两个值,并打印
def fib(a,b,c): if a > c: return print(a,end=" ") fib(b,a+b,c) fib(0,1,388)
法三:非递归方法实现
def fib2(max): a=0 b=1 while a< max: yield a a, b=b, a+b g = fib2(500) for i in g: print(i,end=" ")
4.3 汉诺塔
def hannuota(n,A="A",B="B",C="C"): if n == 1: print(f"将第{n}块积木从{A}柱放到{C}柱") return hannuota(n-1,A,C,B) print(f"将{n}块积木从{A}柱子放到{C}柱子") hannuota(n-1,B,A,C) n = input("请输入汉诺塔层数:") if n.isdigit(): n = int(n) hannuota(n) else: print("请输入数字")
五、查找与排序
5.1 二分法
算法:是高效解决问题的办法
算法之二分法
需求:有一个按照从小到大顺序排列的数字列表
需要从该数字列表中找到我们想要的那个一个数字
如何做更高效???
方案一:整体遍历---效率太低
for num in nums: if num == find_num: print('find it') break
方案二:二分法
思路:
def binary_search(find_num,列表): mid_val=找列表中间的值 if find_num > mid_val: # 接下来的查找应该是在列表的右半部分 列表=列表切片右半部分 binary_search(find_num,列表) elif find_num < mid_val: # 接下来的查找应该是在列表的左半部分 列表=列表切片左半部分 binary_search(find_num,列表) else: print('find it')
实现:
nums=[-3,4,7,10,13,21,43,77,89] find_num=8 def binary_search(find_num,l): print(l) if len(l) == 0: print('找的值不存在') return mid_index=len(l) // 2 if find_num > l[mid_index]: # 接下来的查找应该是在列表的右半部分 l=l[mid_index+1:] binary_search(find_num,l) elif find_num < l[mid_index]: # 接下来的查找应该是在列表的左半部分 l=l[:mid_index] binary_search(find_num,l) else: print('find it') binary_search(find_num,nums)
5.2 快速排序
l = [12,5,48,99,37,26,0,7,51] def Sort(l,low,high):
flag = l[low] i = low j = high # 若i<j 则需要继续找flag位置,并递归 if i < j: # 循环查找,直到i=j,找到flag位置 while i < j: while i < j and l[j] >= flag: j -= 1 if i < j: l[i] = l[j] i += 1 while i < j and l[i] <= flag: i += 1 if i < j: l[j] = l[i] j -= 1 l[i] = flag # if i == low: # # Sort(l,low,i-1) # Sort(l,i+1,high) # elif i == high: # Sort(l,low,i-1) # # Sort(l, i + 1, high) # else: # Sort(l,low,i-1) # Sort(l, i+1, high) if low < i -1: # 若 low < i-1 则至少还有两个元素,继续进行排序。若只有一个则不再进入递归,开始往回递推 Sort(l,low,i-1) if high > i+1: # 同上 Sort(l, i + 1, high) print(l[0]) Sort(l,0,len(l)-1) print(l)