欢迎访问~原文出处——博客园-zhouzhendong
去博客园看该题解
题目传送门 - BZOJ5120
题意概括
原题挺简略的。
题解
本题好难。
听了任轩笛大佬<国家队神犇>的讲课才略会。
然而费用流我也是第一次写。而且这题的费用流是特殊的(简化的)。
于是我抄了任爷的代码。
然而,我因为常量写错,找了一个小时……
这里的work和add我都是直接抄的……懒得打,打完还不一定找得出。反正做法是懂了。
本题很坑。
对于40分,还是比较好拿的,插头dp+滚动(然而我忘记开滚动炸了内存……)就可以了。(代码在最后)
据说插头dp+map可以卡到100?
这里讲标算做法。
我们考虑网络流。
对于两个管口相接,我们只需要建一条流量为1的边。
但是每一个格子的管子都会转。(除了直线)
然而旋转需要费用。
所以我们考虑在自身旋转后,建边要加上费用。
我们设一个格子的4个接口分别为a,b,c,d,如下图:
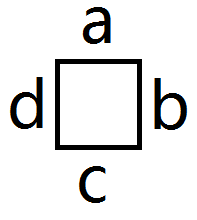
如果分情况讨论,那么实在麻烦。实际上我们可以通过自身连边来完成旋转。
首先我们考虑管子的本质情况:有7种。那么我们可以有相印的连边方案。(二元组中左边为容量,右边为费用)

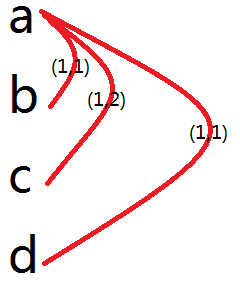


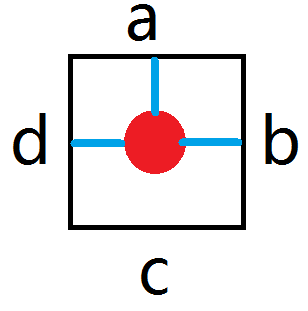
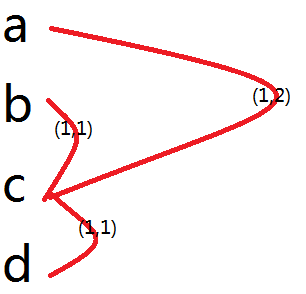
 这个……自身建图是不用的。
这个……自身建图是不用的。
 这个,以及下面的那个建不出图,所以题目说了不能转;哈哈哈哈哈哈哈
这个,以及下面的那个建不出图,所以题目说了不能转;哈哈哈哈哈哈哈

还有一种情况是空的,那么也是不需要自身转移的。
通过自身转移的建图,我们就可以通过费用来完成旋转。
然后就是源点的建边,汇点的建边。
当然,别忘记,对于每一个格子。
然而,我们要记得连上连接接口的边。
但是我们发现,这个不仔细考虑会错掉。
我们把格子按照(行号+列号)的奇偶性黑白染色。
我们发现黑格子的管子一定是接上白格子的。
于是我们人为规定,让流从黑格子流向白格子。
这样就能确定某一个节点(其实就是方格边上的4点)是从源点流来还是流向汇点了。
最后感叹一句:这样做真妙啊!
代码
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#include <map>
using namespace std;
typedef long long LL;
const int NM=2005,N=8205,M=N*20,Inf=2333333;
int dx[4]={-1, 0, 1, 0};
int dy[4]={ 0, 1, 0,-1};
struct Edge{
int x,y,z,flow,nxt;
Edge (){}
Edge (int a,int b,int c,int d,int e){
x=a,y=b,z=c,flow=d,nxt=e;
}
}E[M];
int n,m,S,T,cnt,tot,res,ans,sum;
int id[NM][NM][4],dis[N],vis[N],fst[N],Q[N],pre[N];
int cnt_bit_1(int x){
int ans=0;
while (x)
ans+=x&1,x>>=1;
return ans;
}
bool check_block(int x,int y){
return 1<=x&&x<=n&&1<=y&&y<=m;
}
void Add_Edge(int x,int y,int flow,int z){
E[++cnt]=Edge(x,y,z,flow,fst[x]),fst[x]=cnt;
E[++cnt]=Edge(y,x,-z,0,fst[y]),fst[y]=cnt;
}
void Add(int x,int y,int flow,int z,int color){
if (color==1)
Add_Edge(x,y,flow,z);
else if (x==S)
Add_Edge(y,T,flow,z);
else
Add_Edge(y,x,flow,z);
}
void work(int i,int j,int type,int dir,int color){
int *A=id[i][j];
if (type==1){
Add(S,A[dir],1,0,color);
Add(A[dir],A[(dir+1)%4],1,1,color);
Add(A[dir],A[(dir+2)%4],1,2,color);
Add(A[dir],A[(dir+3)%4],1,1,color);
}
if (type==2){
Add(S,A[dir],1,0,color);
Add(S,A[(dir+1)%4],1,0,color);
Add(A[dir],A[(dir+2)%4],1,1,color);
Add(A[(dir+1)%4],A[(dir+3)%4],1,1,color);
}
if (type==3){
Add(S,A[dir],1,0,color);
Add(S,A[(dir+2)%4],1,0,color);
}
if (type==4){
Add(S,A[dir],1,0,color);
Add(S,A[(dir+1)&3],1,0,color);
Add(S,A[(dir+2)&3],1,0,color);
Add(A[dir],A[(dir+3)&3],1,1,color);
Add(A[(dir+1)&3],A[(dir+3)&3],1,2,color);
Add(A[(dir+2)&3],A[(dir+3)&3],1,1,color);
}
if (type==5){
Add(S,A[dir],1,0,color);
Add(S,A[(dir+1)%4],1,0,color);
Add(S,A[(dir+2)%4],1,0,color);
Add(S,A[(dir+3)%4],1,0,color);
}
}
bool SPFA(){
int head=0,tail=0,qmod=8191;
int x,y;
memset(vis,0,sizeof vis);
memset(dis,63,sizeof dis);
memset(pre,0,sizeof pre);
Q[tail=(tail+1)&qmod]=S;
dis[S]=0,vis[S]=1,pre[S]=0;
while (head!=tail){
vis[x=Q[head=(head+1)&qmod]]=0;
for (register int i=fst[x];i;i=E[i].nxt)
if (E[i].flow&&dis[x]+E[i].z<dis[y=E[i].y]){
dis[y]=dis[x]+E[i].z;
pre[y]=i;
if (!vis[y]){
vis[y]=1;
Q[tail=(tail+1)&qmod]=y;
}
}
}
return dis[T]<Inf;
}
void Flowing(){
for (register int i=pre[T];i;i=pre[E[i].x])
E[i].flow--,E[i^1].flow++;
ans++,res+=dis[T];
}
int main(){
scanf("%d%d",&n,&m);
memset(fst,0,sizeof fst);
tot=sum=0,cnt=1;
S=++tot,T=++tot;
for (int i=1;i<=n;i++)
for (int j=1,x;j<=m;j++){
scanf("%d",&x);
for (int k=0;k<4;k++)
id[i][j][k]=++tot;
if (x==1) work(i,j,1,0,(i+j)&1);
if (x==2) work(i,j,1,1,(i+j)&1);
if (x==3) work(i,j,2,0,(i+j)&1);
if (x==4) work(i,j,1,2,(i+j)&1);
if (x==5) work(i,j,3,0,(i+j)&1);
if (x==6) work(i,j,2,1,(i+j)&1);
if (x==7) work(i,j,4,0,(i+j)&1);
if (x==8) work(i,j,1,3,(i+j)&1);
if (x==9) work(i,j,2,3,(i+j)&1);
if (x==10) work(i,j,3,1,(i+j)&1);
if (x==11) work(i,j,4,3,(i+j)&1);
if (x==12) work(i,j,2,2,(i+j)&1);
if (x==13) work(i,j,4,2,(i+j)&1);
if (x==14) work(i,j,4,1,(i+j)&1);
if (x==15) work(i,j,5,0,(i+j)&1);
sum+=cnt_bit_1(x);
}
for (int i=1;i<=n;i++)
for (int j=1;j<=m;j++)
if ((i+j)&1)
for (int k=0;k<4;k++){
int x=i,y=j;
int x_=i+dx[k],y_=j+dy[k];
if (!check_block(x_,y_))
continue;
Add_Edge(id[x][y][k],id[x_][y_][(k+2)%4],1,0);
}
ans=res=0;
while (SPFA())
Flowing();
printf("%d",(ans*2==sum)?res:-1);
return 0;
}
40分的插头dp
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cmath>
using namespace std;
const int N=2005,M=20,S=1<<17,Inf=100000;
int n,m,b[N],a[N],dp[2][S];
int Ha(int a,int b){
//1<=a<=n,1<=b<=m
return (a-1)*m+b-1 + 1;
}
void Hab(int v,int &a,int &b){
v--;
a=v/m+1;
b=v%m+1;
}
int rotate(int v,int k){
return ((v>>k)|(v<<(4-k)))&15;
}
int main(){
bool tag=0;
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++)
for (int j=1;j<=m;j++)
scanf("%d",&b[Ha(i,j)]);
if (n<m)
tag=1;
if (tag==1){
swap(n,m);
for (int i=1;i<=n;i++)
for (int j=1;j<=m;j++)
a[Ha(i,j)]=rotate(b[(m-j)*n+i],3);/*b[(m-j)*n+i]*/
// (m-j+1,i)
}
else
for (int i=1;i<=n*m;i++)
a[i]=b[i];
/* for (int i=1;i<=n;i++,puts(""))
for (int j=1;j<=m;j++)
printf("%d ",a[Ha(i,j)]);*/
memset(dp,63,sizeof dp);
dp[0][0]=0;
int s=1<<(m+1),x1=0,x0=1;
for (int i=1;i<=n*m;i++){
x1^=1,x0^=1;
memset(dp[x1],63,sizeof dp[x1]);
int x,y,cost;
Hab(i,x,y);
for (int j=0;j<s;j++){
if (dp[x0][j]>Inf)
continue;
if (a[i]==5){
if ((j&1)||!((j>>y)&1))
continue;
dp[x1][j]=min(dp[x1][j],dp[x0][j]);
continue;
}
if (a[i]==10){
if (y==m)
continue;
if (!(j&1)||((j>>y)&1))
continue;
dp[x1][j]=min(dp[x1][j],dp[x0][j]);
continue;
}
for (int k=0;k<4;k++){
int dir=rotate(a[i],k);
int a1=dir&1,a2=(dir>>1)&1,a3=(dir>>2)&1,a4=(dir>>3)&1;
if ((a1^((j>>y)&1))||(a4^(j&1))||(y==m&&a2))
continue;
int j_=((j&(s-2))|a2)&(s-1-(1<<y))|(a3<<y);
dp[x1][j_]=min(dp[x1][j_],dp[x0][j]+(k==3?1:k));
}
}
}
/* for (int i=0;i<=n*m;i++,puts(""))
for (int j=0;j<s;j++)
printf("%10d ",dp[i][j]);*/
int ans=dp[x1][0];
if (ans>Inf)
ans=-1;
printf("%d",ans);
return 0;
}