The Designer
Time Limit: 8000/4000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1115 Accepted Submission(s): 217
Problem Description
Nowadays, little haha got a problem from his teacher.His teacher wants to design a big logo for the campus with some circles tangent with each other. And now, here comes the problem. The teacher want to draw the logo on a big plane. You could see the example of the graph in the Figure1
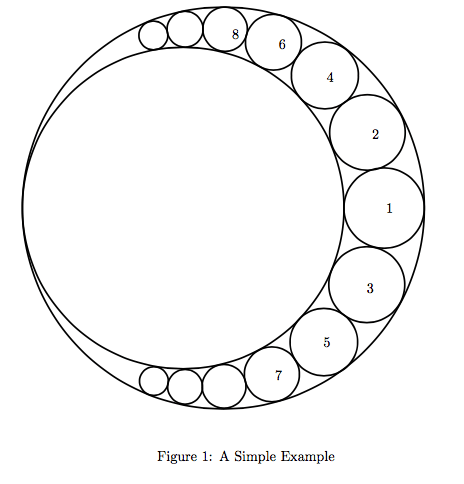
At first, haha's teacher gives him two big circles, which are tangent with each other. And, then, he wants to add more small circles in the area where is outside of the small circle, but on the other hand, inside the bigger one (you may understand this easily if you look carefully at the Figure1.
Each small circles are added by the following principles.
* you should add the small circles in the order like Figure1.
* every time you add a small circle, you should make sure that it is tangented with the other circles (2 or 3 circles) like Figure1.
The teacher wants to know the total amount of pigment he would use when he creates his master piece.haha doesn't know how to answer the question, so he comes to you.
Task
The teacher would give you the number of small circles he want to add in the figure. You are supposed to write a program to calculate the total area of all the small circles.

At first, haha's teacher gives him two big circles, which are tangent with each other. And, then, he wants to add more small circles in the area where is outside of the small circle, but on the other hand, inside the bigger one (you may understand this easily if you look carefully at the Figure1.
Each small circles are added by the following principles.
* you should add the small circles in the order like Figure1.
* every time you add a small circle, you should make sure that it is tangented with the other circles (2 or 3 circles) like Figure1.
The teacher wants to know the total amount of pigment he would use when he creates his master piece.haha doesn't know how to answer the question, so he comes to you.
Task
The teacher would give you the number of small circles he want to add in the figure. You are supposed to write a program to calculate the total area of all the small circles.
Input
The first line contains a integer t(1≤t≤1200), which means the number of the test cases. For each test case, the first line insist of two integers R1 and R2 separated by a space (1≤R≤100), which are the radius of the two big circles. You could assume that the two circles are internally tangented. The second line have a simple integer N (1≤N≤10 000 000), which is the number of small circles the teacher want to add.
Output
For each test case:
Contains a number in a single line, which shows the total area of the small circles. You should out put your answer with exactly 5 digits after the decimal point (NO SPJ).
Contains a number in a single line, which shows the total area of the small circles. You should out put your answer with exactly 5 digits after the decimal point (NO SPJ).
Sample Input
2
5 4
1
4 5
1
Sample Output
3.14159
3.14159
Source
Recommend
题目大意:求那些相切的n个圆的面积
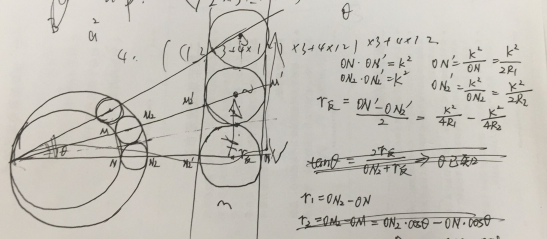
题解:利用反演,一和二 ,的性质,具体看本博客反演的归纳
草稿图:
如果只是枚举i从1到n是2000+ms,枚举2的步长就降低一半到了1000+ms
#include<bits/stdc++.h> using namespace std; const double eps=1e-13; double pi=acos(-1.0); double ans,R1,R2,k,rr,r1; int n,T; int main() { scanf("%d",&T); while(T--) { scanf("%lf%lf",&R1,&R2); scanf("%d",&n); if (R1>R2) swap(R1,R2); double k=1; //k可以取任意值 double rr=k*k/(4*R1)-k*k/(4*R2); //反形圆半径 double lx=k*k/(2*R2)+rr; //反形圆的圆心到反演点的距离 ans=pi*(R2-R1)*(R2-R1); //因为n>=1 for(int i=2;i<=n;i+=2) { double ly=(i/2)*2*rr; double l=sqrt(lx*lx+ly*ly); //第i个圆的反形圆的圆心到反演点的距离 double r=( k*k/(l-rr)-k*k/(l+rr) )/2.0; //利用反演求第i个圆的圆心 if (pi*r*r<eps) break; if (i+1>n) ans+=pi*r*r; else ans+=pi*r*r*2; } printf("%.5lf ",ans); } }