0.引言
在社会网络分析领域,非常重要的一块就是寻找网络中的有联系的小团体,比较正式的说法是“成分”。通常将图论中最大的连通分量定义为“成分”,成分内部的各点之间必然有一条途径相连,而成分之外的点与成分内部的点没有联系。
1.概念
连通分量是图论非常重要的一个概念。与它有一个相近的概念,叫连通图。对于初学者而言,很容易混淆这两个概念。
(1)连通图是相对整体而言的,连通分量是相对局部子集而言。
(2)连通图只有一个连通分量即本身,非连通的无向图有多个连通分量。
(3)连通分量内部任意两点之间都可达
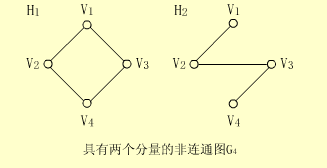
例如:上图是无向图G4,有两个连通分量H1、H2,H1、H2内部任意两点都可达。
2.分组算法
思路1:对于任意给定的无向图G。
step1:随机从中取出一个节点X,添加到集合S1。以x为起点进行广度搜索,将有连接的节点Y和边E添加到集合S1,并将节点E标志位设置为已访问。
step2:从G中剔除集合S1中所有的节点。
step3:重复step1、step2操作,直到G中的节点数为0,由此生成了分组S1、S2......Sn。

1 /** 2 * 根据连通划分分组 3 * @returns {Array} 4 */ 5 GroupDataHelper.prototype.divideGroupByConn = function () { 6 var copyNodes = this.nodes; 7 while (copyNodes.length > 0) { 8 var startId = copyNodes[0].id;//随机从中取出一个节点X,添加到集合S1 9 var group = this.getSingleGroupByNodeId(startId);//以x为起点进行广度搜索 10 this.groups.push(group);//将有连接的节点Y和边E添加到集合S1 11 removeGroupFromNodes(group.nodes, copyNodes);//从G中剔除集合S1中所有的节点 12 } 13 return this.groups; 14 } 15 16 /** 17 * 根据节点Id获取单个分组 18 * @param nodeId 19 * @returns {{nodes: Array, edges: Array}} 20 */ 21 GroupDataHelper.prototype.getSingleGroupByNodeId = function (nodeId) { 22 var group = {nodes: [], edges: []}; 23 var startNode = this.nodesMap[nodeId]; 24 group.nodes.push(startNode); 25 this.travelGraphByBFS([startNode], group); 26 return group; 27 }; 28 29 /** 30 * 广度搜索,得到一个连通分量 31 * @param nodeArr 32 * @param result 33 */ 34 GroupDataHelper.prototype.travelGraphByBFS = function (nodeArr, group) { 35 var nextNodeArr = []; 36 for (var i = 0; i < nodeArr.length; i++) { 37 var node = nodeArr[i]; 38 node.isVisited = true; 39 var neighbours = node.neighbours; 40 if (neighbours && neighbours.length > 0) { 41 for (var j = 0; j < neighbours.length; j++) { 42 var neighbour = neighbours[j]; 43 if (neighbour.isVisited == false) { 44 var temp = this.nodesMap[neighbour.id]; 45 group.nodes.push(temp); 46 group.edges.push(this.edgesMap[temp.id][node.id]); 47 neighbour.isVisited = true; 48 nextNodeArr.push(neighbour); 49 } 50 } 51 } 52 53 } 54 //下一层 55 if (nextNodeArr.length > 0) { 56 this.travelGraphByBFS(nextNodeArr, group); 57 } else { 58 return; 59 } 60 61 };
思路2:对于任意给定的无向图G。采用并查集的思路,可以解决连通性问题。并查集是由一个数组pre[]和两个函数构成的。第一个函数为find()函数,用于寻找前导点的,第二个函数是join()用于合并路线的。我们只需要遍历G的边集合,使用join()函数将边的两个端点合并路线,由此可以得到多棵数。然后遍历点集合使用find()函数将节点的分组ID设置为前导节点Id即可完成分组。

** * 并查集:查找前导节点 * @param x * @returns {*} */ function find(x) { var r = x; while (pre[r] != r) r = pre[r];//找到他的前导结点 var i = x, j; while (i != r)//路径压缩算法 { j = pre[i];//记录x的前导结点 pre[i] = r;//将i的前导结点设置为r根节点 i = j; } return r; } /** * 并查集:合并路线 * @param x * @param y */ function join(x, y) { var a = find(x);//x的根节点为a var b = find(y);//y的根节点为b if (a != b)//如果a,b不是相同的根节点,则说明ab不是连通的 { pre[a] = b;//我们将ab相连 将a的前导结点设置为b } } /** * 获取分组 * @param data */ function getGroups(data) { var i=0; var nodes = data.nodes.length; var edges = data.edges.length; //初始化前导节点 for(var i=0;i<nodes.length;i++){ var node = nodes[i]; pre[node.index] = node.index;//前导节点初始为自己 } //遍历边集合,合并 for(i=0;i<edges.length;i++){ var edge = edges[i]; var sNode = nodesMap[edge.source]; var tNode = nodesMap[edge.target]; join(sNode.index,tNode.index); } //遍历点集合,设置分组ID for(i=0;i<nodes.length;i++){ var node = nodes[i]; node.groupId = find(node.index); } }
3.性能比较

其中,k表示分组数量,n表示节点数量,m表示边数量
思路1的时间复杂度:O(k*n*logn+m)
思路2的时间复杂度:最好的情况下为O(m+n),最差的情况下为O(m*logn+m)
结论:在边数量远远大于节点数量,且分组比较少时,优先考虑思路1;在节点数量、分组数比较多时,优先考虑思路2
4.参考资料
连通分量:https://blog.csdn.net/qq_33913037/article/details/71213985?locationNum=1&fps=1
蓝桥杯算法:https://blog.csdn.net/The_best_man/article/details/62418823
networkX: https://blog.csdn.net/Eastmount/article/details/78452581
igraph: https://blog.csdn.net/yepeng2007fei/article/details/78250088
社会网络分析:http://blog.sina.com.cn/s/blog_dc8ea6c10101l2lc.html
成分:http://blog.sina.com.cn/s/blog_6249651d0100la5r.html
阿里云I+关系网络分析:https://blog.csdn.net/yunqiinsight/article/details/80134024
数据可视化:http://baijiahao.baidu.com/s?id=1600865025454038979&wfr=spider&for=pc
