排序（上）：如何分析一个"排序算法"？

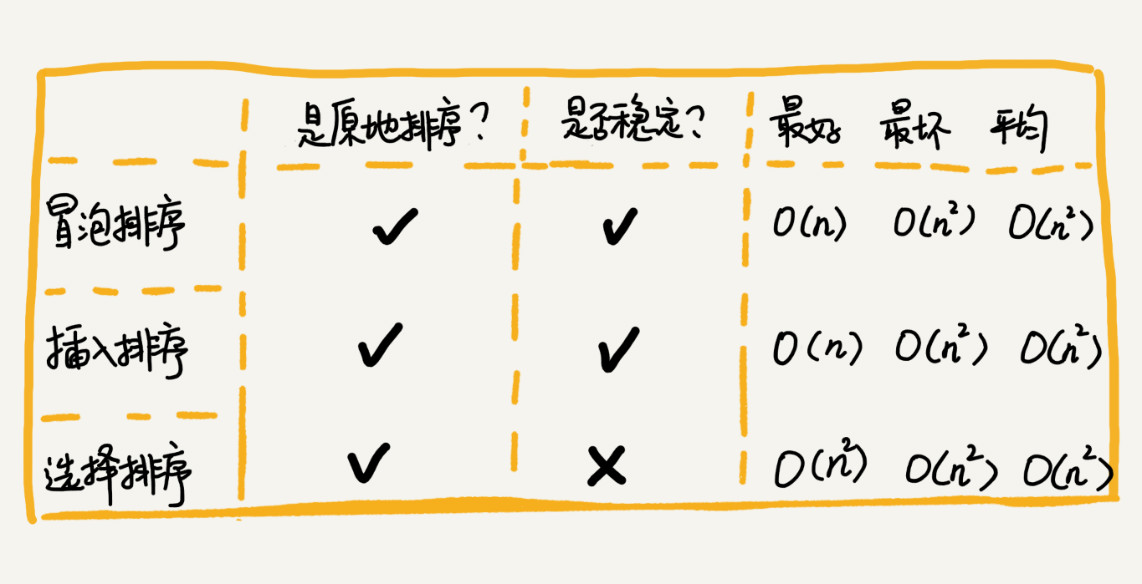
如何分析一个"排序算法"？

执行效率

对于排序算法执行效率分析一般会从几个方面来衡量：

1.最好情况、最坏情况、平均情况时间复杂度

对于排序数据的有序度不同，排序算法在的性能表现会有影响，所以需要分析不同情况下的时间复杂度

2.时间复杂度的系数、常数、低阶

时间复杂度反应的是代码执行时间随数据规模增长的变化趋势，在实际软件开发中，排序的数据规模可能很小，在对比同一阶时间复杂度的排序算法性能的时候，就需要把系数、常数、低阶也一起考虑进去。

3.比较次数和交换（或移动）次数

内存消耗

算法的内存消耗可以通过空间复杂度来衡量，空间复杂度O(1)的排序算法称为“原地排序”。

稳定性

稳定性描述在待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。

一、冒泡排序

算法思路：每次比较相邻两个元素，根据大小关系判断是否需要互换，每次冒泡会让至少一个元素移动到它应该在的位置，重复n次直到排序完成。

        public static void bubbleSort(int[] iarray)
        {
            if (iarray.Length <= 1) return;

            // 记录最后一次交换的位置
            int lastChangeIndex = 0;
            // 无序数列的边界
            int sortBorder = iarray.Length - 1;
            int length = iarray.Length - 1；
            for(int i = 0; i < length; i++)
            {
                // 提前退出标志位
                bool isSorted = true;
                for(int j = 0; j < sortBorder; j++)
                {
                    if (iarray[j] > iarray[j + 1])
                    {
                        int tmp = iarray[j];
                        iarray[j] = iarray[j + 1];
                        iarray[j + 1] = tmp;
                        isSorted = false;
                        // 把无序数列的边界更新为最后一次交换元素的位置
                        lastChangeIndex = j;
                    }
                }
                if (isSorted) break;
            }
        }

1.冒泡过程只涉及相邻数据的比较、交换操作，只需要常量级的临时空间，所以空间复杂度是O(1)，是原地排序算法。

2.在冒泡排序中，只有交换才会改变两个元素的前后顺序，当相邻两个元素相等时，我们不做交换，就不会改变元素前后顺序，所以是稳定的排序算法。

3.冒泡排序的时间复杂度

如果用概率论方法分析冒泡排序的平均时间复杂度会很复杂，我们可以通过“有序度”和“逆序度”来分析。

有序度是数组中具有有序关系的元素对的个数

逆序度与有序度相反，是逆序关系的元素对的个数

满有序度是指完全有序的数组的有序度个数，n*(n-1)/2

逆序度 = 满有序度 - 有序度

冒泡排序包含比较和交换两个操作，每交换一次，有序度加1，不管算法如何改进，交换次数总是确定的，即为逆序度，也就是n*(n-1)/2-初始有序度，上面的例子中就是15-3=12，要进行12次交换操作。

平均情况下交换次数取中间值，也就是n(n-1)/4，而在排序过程中，比较操作肯定比交换操作多，而复杂度上限为O(n²)，所以平均情况下时间复杂度就是O(n²)。

二、插入排序

算法思路：将数组中的数据分为两个区间，已排序区间和未排序区间，初始已排序区间只有一个元素，就是数组的第一个元素，接着取未排序区间中的元素在已排序区间中找到合适的位置将其插入，并保证已排序区间数据一直有序，重复这个过程直到未排序区间中元素为空，算法结束。

 

public static void insertionSort(int[] iarray)
{
    if(iarray.Length<=1)
        return;
    int length = iarray.Length;
    for(int i=1;i<length;i++)
    {
        int value = iarray[i];
        int j=i-1;
        for(;j>=0;j--)
        {
            if(iarray[j]>value)
                iarray[j+1] = iarray[j]; //数据移动
            else
                break;
        }
        //插入数据
        iarray[j+1] = value;
    }
}

1.插入排序算法运行并不需要额外的存储空间，所以空间复杂度是O(1)，是原地排序算法。

2.插入排序中，对于值相同的元素，我们可以将后面出现的元素插入到前面出现元素的后面，这样就能保证原有的前后顺序不变，所以是稳定排序算法。

3.如果待排序的数组是有序的，我们并不需要移动任何数据，从尾到头在有序数据里面查找插入位置，每次只需要比较一个数据就能确定数据的插入位置，所以最好情况时间复杂度为O(n)；(由于每次都是将数据插入到有序区间，所以从尾部开始比较数据就可确定数据是否需要交换)；如果待排序的数组是无序的，那么每次插入数据都相当于在数组的第一个位置插入新的数据，需要移动大量的数据，所以最坏情况时间复杂度为O(n²)。

在数组中插入一个数据的平均时间复杂度是O(n)，对于插入排序来说，每次插入操作都相当于在数组中插入一个数据，循环执行n次插入操作，所以平均时间复杂度为O(n²)。

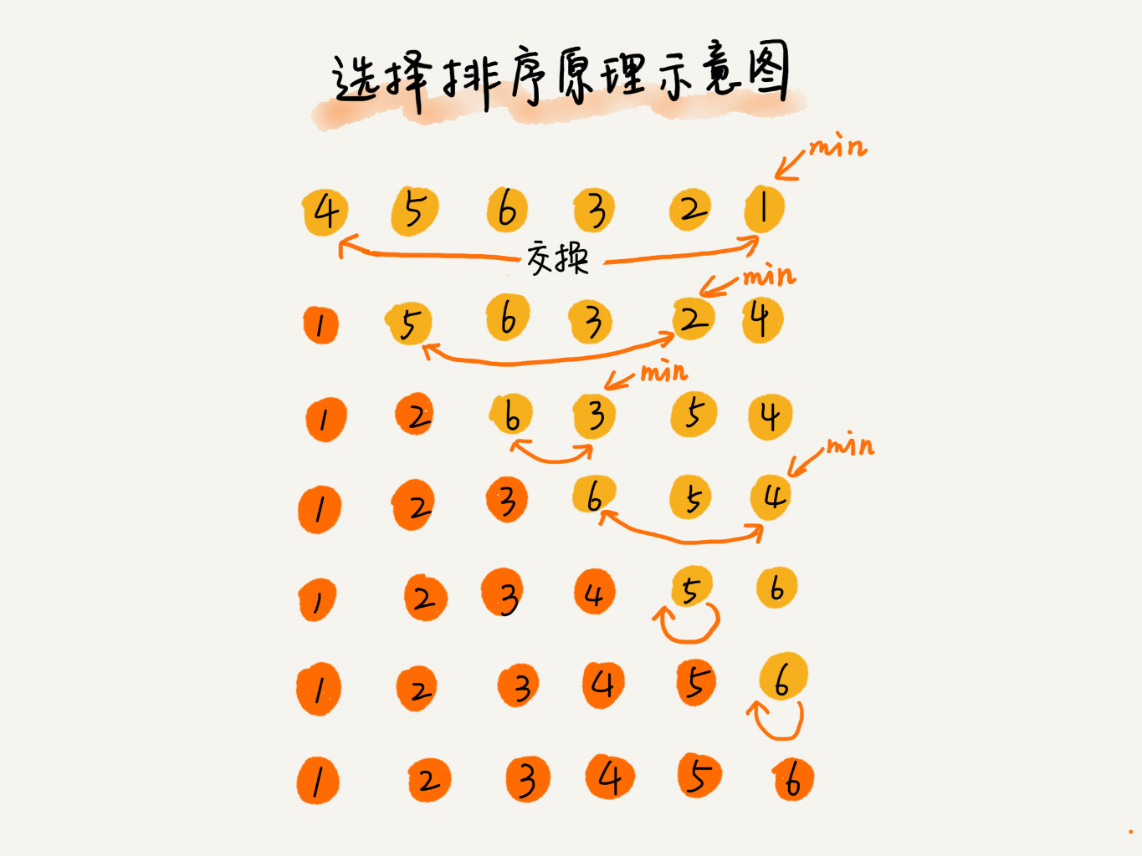
三、选择排序

思路：将待排序数组分为已排序区间和未排序区间，每次从未排序区间中找到最小的元素，将其放到已排序区间的末尾。

public static void insertionSort(int[] iarray)
{
    if(iarray.Length<=1)
        return;
    int length = iarray.Length;
    for(int i=0;i<length-1;i++)
    {
        // 查找最小值
        int minIndex = i;
        for(int j=i+1;j<length;j++)
        {
            if(iarray[j]<iarray[minIndex])
                minIndex = j;
        }
        int tmp = iarray[i];
        iarray[i] = iarray[minIndex];
        iarray[minIndex] = tmp;
    }
}

1.选择排序算法空间复杂度是O(1)，是原地排序算法。

2.选择排序最好情况、最坏情况、平均情况时间复杂度都是O(n²)。

3.选择排序是不稳定排序算法。

针对冒泡排序与插入排序的对比，冒泡排序不管如何优化，元素交换的次数是一个固定值，也就是原始数据的逆序度。插入排序也是同样的，不管如何优化，元素移动的次数也等于原始数据的逆序度。

但是从代码实现上来看，冒泡排序的数据交换比插入排序的数据移动要复杂，需要3个赋值操作，而插入排序只需要1个排序操作，假设执行一个赋值语句的时间粗略的计为单位时间，用冒泡排序和插入排序对同一个逆序度为K的数组进行排序。用冒泡排序需要K次交换操作，总计3*K单位时间，而插入排序只需要K个单位时间。

所以在实际软件开发中，会优先选择插入排序。