User ainta has a permutation p1, p2, ..., pn. As the New Year is coming, he wants to make his permutation as pretty as possible.
Permutation a1, a2, ..., an is prettier than permutation b1, b2, ..., bn, if and only if there exists an integer k (1 ≤ k ≤ n) where a1 = b1, a2 = b2, ..., ak - 1 = bk - 1 and ak < bk all holds.
As known, permutation p is so sensitive that it could be only modified by swapping two distinct elements. But swapping two elements is harder than you think. Given an n × n binary matrixA, user ainta can swap the values of pi and pj (1 ≤ i, j ≤ n, i ≠ j) if and only if Ai, j = 1.
Given the permutation p and the matrix A, user ainta wants to know the prettiest permutation that he can obtain.
The first line contains an integer n (1 ≤ n ≤ 300) — the size of the permutation p.
The second line contains n space-separated integers p1, p2, ..., pn — the permutation p that user ainta has. Each integer between 1 and n occurs exactly once in the given permutation.
Next n lines describe the matrix A. The i-th line contains n characters '0' or '1' and describes the i-th row of A. The j-th character of the i-th line Ai, j is the element on the intersection of the i-th row and the j-th column of A. It is guaranteed that, for all integers i, j where 1 ≤ i < j ≤ n, Ai, j = Aj, i holds. Also, for all integers i where 1 ≤ i ≤ n, Ai, i = 0holds.
In the first and only line, print n space-separated integers, describing the prettiest permutation that can be obtained.
7
5 2 4 3 6 7 1
0001001
0000000
0000010
1000001
0000000
0010000
1001000
1 2 4 3 6 7 5
5
4 2 1 5 3
00100
00011
10010
01101
01010
1 2 3 4 5
In the first sample, the swap needed to obtain the prettiest permutation is: (p1, p7).
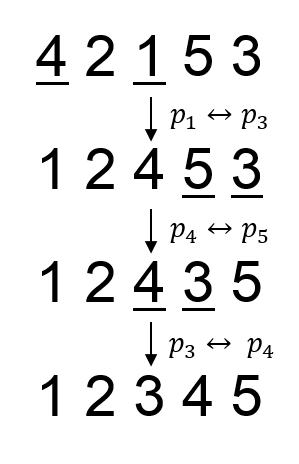
In the second sample, the swaps needed to obtain the prettiest permutation is (p1, p3), (p4, p5), (p3, p4).
A permutation p is a sequence of integers p1, p2, ..., pn, consisting of n distinct positive integers, each of them doesn't exceed n. The i-th element of the permutation p is denoted as pi. The size of the permutation p is denoted as n.
这题是给出交换矩阵,求交换完字典序最小
原来我是这样想的
n^2暴力枚举i<j,a[i]>a[j]的一对交换,换到最后没了就好了。这样每次至少减少1逆序对,做n次不就完了吗 恩才n^3可以接受
(阿连哭死在厕所)
妈蛋当时我到底在想什么……逆序对个数是n^2啊……要n^4不爆才怪
我们发现如果a[i]、a[j]可以互换,那么i和j是连通的。在同一联通块中的元素都是可以互换的
联通块可以直接用并查集或者floyd搞出来
然后从小到大枚举每一个位置,用它所在联通块中没取到的最小元素填进去
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<set>
#include<map>
#include<ctime>
#include<iomanip>
#define LL long long
#define inf 0x7ffffff
#define N 200010
using namespace std;
inline LL read()
{
LL x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n;
int a[1010];
bool mrk[1010];
bool p[1010][1010];
int main()
{
n=read();
for (LL i=1;i<=n;i++)a[i]=read();
for (int i=1;i<=n;i++)
{
char ch[1010];scanf("%s",ch+1);
for (int j=1;j<=n;j++)
if (ch[j]=='1')p[i][j]=1;
p[i][i]=1;
}
for (int k=1;k<=n;k++)
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++)
if(p[i][k]&&p[k][j])p[i][j]=1;
memset(mrk,1,sizeof(mrk));
for (int i=1;i<=n;i++)
{
int mn=inf,res=0;
for (int j=1;j<=n;j++)
if (mrk[j]&&p[i][j]&&a[j]<mn)
{
mn=a[j];
res=j;
}
mrk[res]=0;
printf("%d ",mn);
}
return 0;
}