312、戳气球问题
基本思想:
动态规划
具体实现:
1、确认状态
最后一步---dp[i][j]=x,戳破气球i和气球j之间的所有气球(不包括i和j),可以获得的最高分数为x。
设两个虚拟气球,气球0和气球n+1
子问题---最后一个被戳破的气球为k,子问题就是dp[i][k],dp[k][j]
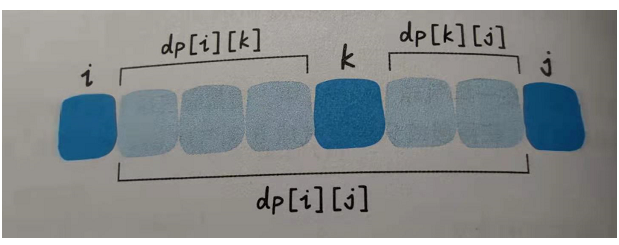
2、状态转移方程
dp[i][j]=dp[i][k]+dp[k][j]+points[i]*points[k]*points[j]
3、初始状态
数组都初始化为0
4、计算顺序
从左到右,从下到上
因为最后的答案是dp[0][n+1]
代码:
class Solution: def maxCoins(self, nums: List[int]) -> int: n = len(nums) points = [0]*(n+2) points[0] = points[n+1] = 1 # 虚拟气球 for i in range(1,n+1): points[i] = nums[i-1] dp = [[0]*(n+2) for _ in range(n+2)] for i in range(n,-1,-1): for j in range(i+1,n+2): for k in range(i+1,j): dp[i][j] = max(dp[i][j],dp[i][k]+dp[k][j]+points[i]*points[j]*points[k]) return dp[0][n+1]