题目描述
小明在他的果园种了一些苹果树,这些苹果树排列成一个圆。为了保证苹果的品质,在种植过程中要进行疏果操作。为了更及时地完成疏果操作,小明会不时地检查每棵树的状态,根据需要进行疏果。检查时,如果发现可能有苹果从树上掉落,小明会重新统计树上的苹果个数(然后根据之前的记录就可以判断是否有苹果掉落了)。在全部操作结束后,请帮助小明统计相关的信息。
输入格式
从标准输入读入数据。
第1行包含一个正整数N,表示苹果树的棵数。
第\(1+i\)行\((1\le i \le N)\),每行的格式为\(m_i,a_{i1},a_{i2},...,a_{i,m_{i}}\)。其中,第一个正整数\(m_i\)表示本行后面的整数个数。后续的\(m_i\)个整数表示小明对第\(i\)棵苹果树的操作记录。若\(a_{ij}(1\le j \le m_i)\)为正整数,则表示小明进行了重新统计该棵树上的苹果个数的操作,统计苹果个数为\(a_{ij}\);若为零或负整数,则表示一次疏果操作,去掉苹果个数是\(|a_{ij}|\)。
输入保证一定是正确的,满足:
- \(a_{i1} \gt 0\),即对于每棵树的记录,第一个操作一定是统计苹果个数(初始状态,此时不用判断是否有苹果掉落);
- 每次疏果操作保证操作后树上的苹果个数仍为正。
输出格式
输出到标准输出。
输出只有一行,包含三个整数T、D、E。其中,
- T为全部疏果操作结束后所有苹果树上剩下的苹果总数(假设每棵苹果树在最后一次统计苹果个数操作后苹果不会因为疏果以外的原因减少);
- D为发生苹果掉落的苹果树的棵数;
- E为相邻连续三棵树发生苹果掉落的组数。
对于第三个统计量的解释:N棵苹果树\(A_1,A_2,...A_N\)排列成一个圆,那么\(A_1\)与\(A_2\)相邻,\(A_2\)与\(A_3\)相邻,...... ,\(A_{N-1}\)与\(A_N\)相邻,\(A_{N}\)与\(A_1\)相邻。如果\(A_{i-1},A_i,A_{i+1}\)这三棵树都发生了苹果掉落的情况,则记为一组。形式化的,有
其中, \(\operatorname{Drop}\left(A_{i}\right)\) 表示苹果树 \(A_{i}\) 是否发生苹果掉落的情况, \(\operatorname{Pred}\left(A_{i}\right)\) 表示 \(A_{i}\) 的前一棵树 \(A_{i-1}(\) 如果 \(i>1)\) 或者 \(A_{N}\left(\right.\) 如果 \(i=1\) ) \(, \operatorname{Succ}\left(A_{i}\right)\) 表示 \(A_{i}\) 的向一棵树 \(A_{i+1}(\) 如果 \(i<N)\) 或者 \(A_{1}\) (如果 \(i=N\) )。
样例1输入
4
4 74 -7 -12 -5
5 73 -8 -6 59 -4
5 76 -5 -10 60 -2
5 80 -6 -15 59 0
样例1输出
222 1 0
样例1解释
全部操作结束后,第1棵树上剩下的苹果个数为74-7-12-5=50,第2棵为59-4=55,第3棵为60-2=58,第4棵为59-0=59。因此T=50+55+58+59=222。
其中,第3棵树在第2次统计之前剩下的苹果个数为76-5-10=61>60 ,因此发生了苹果掉落的情况。可以检验其他的树没有这种情况,因此D=1。
没有连续三棵树都有发生苹果掉落的情况,因此E=0。
样例2输入
5
4 10 0 9 0
4 10 -2 7 0
2 10 0
4 10 -3 5 0
4 10 -1 8 0
样例2输出
39 4 2
样例2解释
第1、2、4、5棵树发生了苹果掉落的情况,因此D=4。其中,连续三棵树都发生苹果掉落情况有(5,1,2)和(4,5,1),因此E=2。
子任务
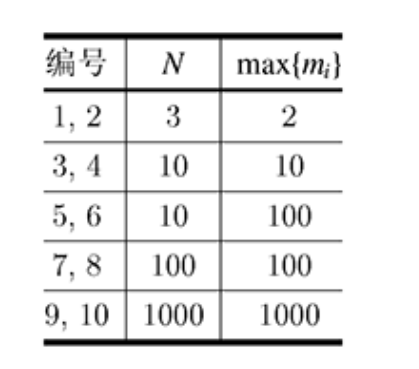
- \(m_i \le 1000\),对所有\(1\le i \le N\)
- \(|a_{ij}| \le 10^6\), 对所有\(1 \le i \le N, 1 \le j \le m_i\)
提示
- 如果你的程序没有实现统计D和E的功能,请按照D=0,E=0输出结果,这样如果T的统计正确能够得到一部分分数。
- 如果你程序没事实现统计E的功能,请按照E=0输出结果,这样如果T的统计正确能够得到一部分分数。
代码
#include <iostream>
#include <vector>
using namespace std;
//定义苹果数结构体
struct appletree
{
//记录nums中的数据个数
int num;
//记录苹果树疏果后剩余的苹果数
vector<int> nums;
//1表示有苹果意外掉落的情况发生,0则表示无掉落情况发生
bool flag;
};
int main()
{
//创建苹果树集合
vector<appletree> appnums;
//N为苹果棵树,M表示改行后面需要输入的整数个数
int N, M;
cin >> N;
//疏果后的剩余的苹果总数
int appsums = 0;
//发生苹果意外掉落的树的棵树
int errornum = 0;
//连续三个树发生苹果掉落情况的组数
int listnum = 0;
for (int i = 0; i < N; i++)
{
cin >> M;
appletree appnum;
appnum.num = 0;
appnum.flag = 0;
int mi;
for (int j = 0; j < M; j++)
{
cin >> mi;
//记录第一次统计苹果树的数量
if (mi > 0 && appnum.num == 0)
{
appnum.nums.push_back(mi);
appnum.num++;
}
//判断是否重新统计,若是则在nums后插入重新统计的数据
else if (mi > 0 && appnum.num > 0)
{
appnum.nums.push_back(mi);
//判断是否发生掉落情况,若是则flag=1
if (mi != appnum.nums[appnum.num - 1])
{
appnum.flag = 1;
}
appnum.num++;
}
//处理疏果情况,更新疏果后的苹果数
else
{
appnum.nums[appnum.num - 1] += mi;
}
}
//记录发生苹果意外掉落的树的棵树
if (appnum.flag == 1)
errornum++;
//所有苹果树疏果后的苹果总数
appsums += appnum.nums[appnum.num - 1];
appnums.push_back(appnum);//将数据添加到苹果树集合中
}
//处理连续三个树发生苹果掉落的情况
for (int i = 0; i < N; i++)
{
//当发现flag=1时表示有苹果意外从树上掉落
if (appnums[i].flag == 1)
{
//判断该树的前后是否flag都等于1,若是则listnum++
if (appnums[(i + 1 + N) % N].flag == 1 && appnums[(i - 1 + N) % N].flag == 1)
{
listnum++;
}
}
}
cout << appsums << " " << errornum << " " << listnum << endl;
return 0;
}