遗传算法基本原理
遗传算法是从代表问题可能潜在解集的一个种群开始的,而一个种群则由经过基因编码的一定数量的个体组成。每个个体实际上是染色体带有特征的实体。作为多个基因的集合,单个染色体是遗传物质的主要载体,其在种群中的命运由其基因组合决定。初始种群产生以后按照优胜劣汰、适者生存的原理,逐代演化产生出越来越好的近似解。在每一代,根据问题域中个体的适应度大小挑选个体,并借助代表于自然遗传学的遗传算子进行交叉和变异,产生出代表新的解集的种群。这个过程导致种群像自然进化一样,后代种群比前代更加适应于环境,末代种群中最优个体经过解码,可以作为问题的近似最优解。
遗传算法采纳了自然进化模型,如选择、交叉、迁移、局域与邻域等。与传统搜索算法不同,遗传算法是从一组随机产生的初始解开始搜索过程。种群中的每个个体是问题的一个解,称为“染色体”,染色体是一串符号,比如二进制01串。这些染色体在后续迭代中不断进化,称为遗传。在每一代中用适应度来测量染色体的好坏。生成的下一代染色体称为后代。后代是由前一代染色体通过交叉或者变异运算形成的。新一代形成中,根据适应度的大小选择部分后代,淘汰部分后代,从而保持种群大小的稳定性。适应度高的染色体被选中的概率高,这样经过若干代之后,算法收敛于最好的染色体,它很可能就是问题的最优解或次优解。
生物遗传与遗传算法概念比对

基本概念
- 染色体:在使用遗传算法时,需要把问题的解编成一个适合的码子。这种具有固定结构的符号串既是染色体。符号串的每一位代表一个基因。符号串的总位数成为染色体的长度,一个染色体就代表问题的一个解,每个染色体也被称为一个个体。
- 群体:每代所产生的染色体总数成为群体,一个群体包含了该问题在这一代的一些解的集合。
- 适应度:对群体中每个染色体进行编码后,每个个体对应一个具体问题的解。而每个解对应于一个函数值。该函数值即适应函数,就是衡量染色体对环境适应度的指标,也是反映实际问题的目标函数。
遗传操作
在前一代群体的基础上产生新一代群体的工作称为遗传操作。基本的遗传操作有如下几种:
- 选择:按一定的概率从上代群体中选择M对个体作为双亲,直接拷贝到下一代,染色体不发生变化。
- 交叉:对于选中进行繁殖的两个染色体X,Y,以X,Y为双亲作交叉操作,从而产生两个后代X1,Y1.
- 变异:对于选中的群体中的个体(染色体)随机选取某一位进行取反运算,即将该染色体码翻转。
用遗传算法求解的过程是根据待解决问题的参数集进行编码,随机产生一个种群,计算适应函数和选择率,进行选择、交叉、变异操作。如果满足收敛条件,此种群为最好个体,否则,对产生的新一代群体重新进行选择、交叉、变异操作,循环往复直到满足条件。
遗传算法的基本步骤
- 确定参变量及其各种约束条件,即确定个体的表现形式和问题的解空间
- 建立优化模型,即确定出求解问题的目标函数和数学描述形式及量化方法
- 确定染色体的编码方法,即确定个体的基因形式
- 确定编码方法,即确定出个体的基因形式到个体的表现形式的对应关系和转化方式
- 确定个体适应度的量化评价方法,即确定出目标函数值同个体适应度的转化规则
- 设计遗传算子,即确定出选择算子,交叉算子和变异算子的具体操作方法
- 确定遗传算法的有关运行参数,即确定出遗传算法
遗传算法流程图
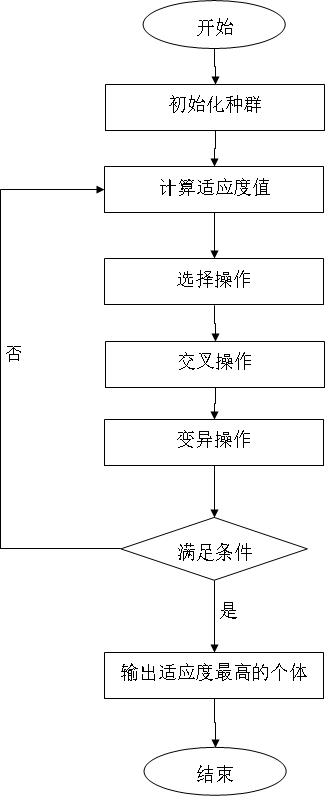
遗传算法的特点
传统的优化方法主要有三种:枚举法、启发式算法和搜索算法。随着问题种类的不同以及问题规模的扩大,需要寻求一种能以有限的代价来解决搜索和优化的通用方法,遗传算法正是为我们提供了一个有效的途径,它不同于传统的搜索和优化方法。主要区别在于:
1.自组织、自适应和自学习性
应用遗传算法求解问题时,在编码方案、适应度函数及遗传算子确定后,算法将利用进化过程中获得的信息自行组织搜索。由于自然选择策略为“适者生存”,因而适应度大的个体具有较高的生存概率。通常,适应度大的个体具有更适应环境的基因结构,在通过基因重组和基因突变等遗传操作,就可能产生更适应环境的后代。
进化算法的这种自组织、自适应特征,使它同时具有能根据环境变化来自动发现环境的特性和规律的能力。自然选择消除了算法设计过程中的一个最大障碍,即需要事先描述问题的全部特点,并要说明针对问题的不同特点算法应采取的措施。
因此,利用遗传算法的方法,我们可以解决那些复杂的非结构化的问题。
2.遗传算法的本质并行性
遗传算法按并行方式搜索一个群数目的点,而不是单点。它的并行性表现在两个方面,一是遗传算法的内在并行性,即遗传算法本身非常适合大规模并行。最简单的并行方式是让N台计算机各自进行独立种群的演化计算,运行过程中甚至不进行任何通信(独立的种群之间若有少量的通信一般会带来更好的结果),等到运算结束才通信比较,选择最佳个体。这种并行处理方式对并行系统结构没有什么限制和要求,可以说,遗传算法适合在目前所有的并行机或分布式吸引上进行并行处理,而且对运行效率没有太大的影响。二是遗传算法的内含并行性。由于遗传算法采用种群的方式组织搜索,因而可同时搜索解空间内的多个区域,并相互交流信息。使用这种搜索方式,虽然每次只执行与种群规模n成比例的计算,但实质上已经进行了大约O(n3)次有效搜索,这就使遗传算法能以较少的计算获得较大的收益。
3.遗传算法不需要求导或其他的辅助知识,而只需要影响搜索方向的目标函数和相应的适应度函数
4.遗传算法强调概率转换规,而不是确定的转换规则
5.遗传算法可以更加直接的应用
6.遗传算法对给定的问题,可以产生许多的潜在解,最终可以由使用者确定
遗传算法编码方法
在遗传算法中如何描述问题的可行解,即把一个问题的可行解从其解空间转换到遗传算法所能处理的搜索空间的转换方法称为编码。De Jong曾提出了两条操作性较强的实用编码原则。
- 编码原则一(有意义积木块编码原则):应使用能易于产生与所求问题相关的且具有低阶,短定义长度的编码方案。
- 编码原则二(最小字符集编码原则):应使用能使问题得到自然表示或描述的具有最小字符集的编码方案。
迄今为止人们已经提出了许多的编码方法,总的来说,可以分为三类:二进制编码方法,浮点数编码方法,符号编码方法。
1.二进制编码
二进制编码方法是遗传算法中最常用的一种编码方法,它使用的编码符号集是由二进制符号0和1组成的二值符号集{0,1},它所构成的个体基因型是一个二进制编码符号串。它有以下优点:
- 编码、解码简单易行。
- 交叉,变异等遗传操作便于实现。
- 符合最小字符集编码原则。
- 便于利用模式定理对算法进行理论分析。
二进制编码符号串的长度与问题所要求的精度有关。
2.格雷码编码
由于二进制不便于反映所求问题的结构特征,对于一些连续函数的优化问题等,也由于遗传运算的随机特性而使得其局部搜索能力较差,因而人们提出了用格雷码来对个体进行编码。
格雷码,连续的两个整数所对应的编码值之间只有一个码位不相同。格雷码有这样一个特点:任意两个整数的差是这两个整数所对应的海明距离。这个特点是遗传算法中使用格雷码进行个体编码的主要原因。格雷码编码主要有以下优点:
- 便于提高遗传算法的局部搜索能力。
- 交叉,变异等遗传操作易于实现。
- 符合最小字符集编码原则。
- 便于用模式定理对算法进行理论分析。
格雷码编码方法是二进制编码方法的一种变型,其编码精度与相同长度二进制编码方法的精度相同。
3.浮点数编码
由于二进制编码存在着连续函数离散化时的映射误差,而且不便于反映所求问题的特定知识,因而人们提出了用浮点数来对个体进行编码。
浮点数编码方法:指个体的每个基因值用某一范围内的一个浮点数来表示个体的编码长度等于其决策变量的个数,个体变量的长度等于去决策变量的真实值,所以也叫真值编码方法。主要有以下优点:
- 适合于在遗传算法中表示范围较大的数。
- 适合于精度较高的遗传算法。
- 便于较大空间的遗传搜索。
- 改善了遗传算法的复杂性,提高了运算效率。
- 便于遗传算法与经典优化方法的混合使用。
- 便于设计针对问题的专门知识的知识型遗传算子。
- 便于处理复杂的决策变量约束条件。
符号编码方法是指个体染色体编码串中的基因值取自一个无数值含义,而只有代码含义的符号集。它的主要优点如下:
- 符合有意义积木块编码原则。
- 便于在遗传算法中利用所求解问题的专门知识。
- 便于遗传算法与相近似算法之间的混合使用。
但对于使用符号编码方法的遗传算法,一般需要认真设计交叉、变异等遗传运算的操作方法,以满足问题的各种约束要求,这样才能提高算法的搜索性能。
4.参数编码
参数编码方法是对含有多个变量的个体进行编码的方法,包含两种编码方法:
- 多参数级联编码方法:将各个参数分别以某种编码方法进行编码,然后再将它们的编码按一定顺序联接在一起就组成了表示全部参数的个体编码。
- 多参数交叉编码方法:将各个参数中起主要作用的码位集中在一起。
遗传算法的应用
遗传算法提供了一种求解复杂系统问题的通用框架,它不依赖于问题的具体领域,对问题的种类有很强的鲁棒性,所以广泛应用于很多科学。
1.函数优化
函数优化是遗传算法的经典应用领域,也是遗传算法进行性能评价的常用算例,人们构造出了各种各样复杂形式的测试函数:连续函数和离散函数、凸函数和凹函数、低维函数和高维函数、单峰函数和多峰函数等。对于一些非线性、多模型、多目标的函数优化问题,用其它优化方法较难求解,而遗传算法可以方便的得到较好的结果。
2.组合优化
随着问题规模的增大,组合优化问题的搜索空间也急剧增大,有时在目前的计算上用枚举法很难求出最优解。对于这类复杂的问题,人们把主要的精力放在研究其近似最优解。