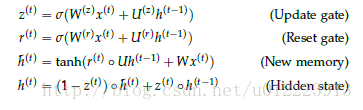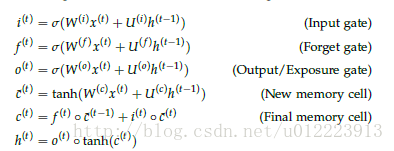2018-10-09,22点58

#下面这一段用一个txt来保存input的信息来模拟input.最后提交代码时候删除这一段即可. a9999=open('1.txt','r') def input(): return a9999.readline().rstrip(' ') #输入数据的一些模板 # n,a=map(int,input().split()) # arr=[int(i)for i in input().split()] # 格式化输出 # print('%.2f'%(maxi/2)) ''' # 最大公约数用 import fractions fractions.gcd(a,b) ''' ''' [编程题] 小易的升级之路 时间限制:1秒 空间限制:32768K #小易经常沉迷于网络游戏.有一次,他在玩一个打怪升级的游戏,他的角色的初始能力值为 a.在接下来的一段时间内,他将会依次遇见n个怪物,每个怪物的防御力为b1,b2,b3...bn. 如果遇到的怪物防御力bi小于等于小易的当前能力值c,那么他就能轻松打败怪物,并 且使得自己的能力值增加bi;如果bi大于c,那他也能打败怪物,但他的能力值只能增加bi 与c的最大公约数.那么问题来了,在一系列的锻炼后,小易的最终能力值为多少? 输入描述: 对于每组数据,第一行是两个整数n(1≤n<100000)表示怪物的数量和a表示小易的初始能力值. 第二行n个整数,b1,b2...bn(1≤bi≤n)表示每个怪物的防御力 import fractions while 1:#处理多段不知道多少的输入用这个方法死循环+内层try except break套路 try: now=input() if now=='': break n,a=map(int,now.split()) for i in range((n)): b=int(input()) if b<=a: a+=b else: a+=fractions.gcd(a,b) print(a) except: break ''' ''' [编程题] 炮台攻击 时间限制:1秒 空间限制:32768K 兰博教训提莫之后,然后和提莫讨论起约德尔人,谈起约德尔人,自然少不了一个人,那 就是黑默丁格------约德尔人历史上最伟大的科学家. 提莫说,黑默丁格最近在思考一个问题:黑默丁格有三个炮台,炮台能攻击到距离它R的敌人 (两点之间的距离为两点连续的距离,例如(3,0),(0,4)之间的距离是5),如果一个炮台能攻击 到敌人,那么就会对敌人造成1×的伤害.黑默丁格将三个炮台放在N*M方格中的点上,并且给出敌人 的坐标. 问:那么敌人受到伤害会是多大? 输入描述: 第一行9个整数,R,x1,y1,x2,y2,x3,y3,x0,y0.R代表炮台攻击的最大距离,(x1,y1),(x2,y2), (x3,y3)代表三个炮台的坐标.(x0,y0)代表敌人的坐标. 输出描述: 输出一行,这一行代表敌人承受的最大伤害,(如果每个炮台都不能攻击到敌人,输出0×) 输入例子1: 1 1 1 2 2 3 3 1 2 输出例子1: 2x while 1: try: r,x1,y1,x2,y2,x3,y3,x0,y0=map(int,input().split()) count=0 if ((x1-x0)**2+(y1-y0)**2)**0.5<=r: count+=1 if ((x2-x0)**2+(y2-y0)**2)**0.5<=r: count+=1 if ((x3-x0)**2+(y3-y0)**2)**0.5<=r: count+=1 print(str(count)+'x') except: break ''' ''' https://www.nowcoder.com/test/question/fe6c73cb899c4fe1bdd773f8d3b42c3d?pid=970447&tid=19242023 牛客网的网站有问题,搜索试卷是出不来的,只能按照连接点进去才行. [编程题] 扫描透镜 时间限制:1秒 空间限制:32768K 在N*M的草地上,提莫种了K个蘑菇,蘑菇爆炸的威力极大,兰博不想贸然去闯,而且蘑菇是隐形的.只 有一种叫做扫描透镜的物品可以扫描出隐形的蘑菇,于是他回了一趟战争学院,买了2个扫描透镜,一个 扫描透镜可以扫描出(3*3)方格中所有的蘑菇,然后兰博就可以清理掉一些隐形的蘑菇. 问:兰博最多可以清理多少个蘑菇? 注意:每个方格被扫描一次只能清除掉一个蘑菇。 输入描述: 第一行三个整数:N,M,K,(1≤N,M≤20,K≤100),N,M代表了草地的大小; 接下来K行,每行两个整数x,y(1≤x≤N,1≤y≤M).代表(x,y)处提莫种了一个蘑菇. 一个方格可以种无穷个蘑菇. 输出描述: 输出一行,在这一行输出一个整数,代表兰博最多可以清理多少个蘑菇. 扫描2次,每一次都找最多的那个3*3进行轰炸即可 地图问题都先加一圈边界,边界上炸弹设置数量为0 #这题目虽然简单,但学到了很多地图上的技巧 while 1: try: n,m,k=map(int,input().split()) save=[[0]*(m+2) for i in range(n+2)] for i in range((k)): a,b=map(int,input().split()) save[a][b]+=1 def search(i,j): #返回save上i,j位置3*3内有多少个地方有地雷 count=0 #先把转移坐标写成列表 arr=[(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1)] for _ in range(len(arr)): newdex=i+arr[_][0],j+arr[_][1] if save[newdex[0]][newdex[1]]>0: count+=1 return count def jian(i,j): #清楚save上i,j位置3*3内每一个地方的一个地雷 #先把转移坐标写成列表 arr=[(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1)] for _ in range(len(arr)): newdex=i+arr[_][0],j+arr[_][1] if save[newdex[0]][newdex[1]]>0: save[newdex[0]][newdex[1]]-=1 #地图实际范围是从1到n 从1到m maxi=0 for i in range(1,(n+1)): for j in range(1,(m+1)): if search(i,j)>maxi: now=i,j maxi=search(i,j) jian(now[0],now[1]) maxi2=0 for i in range((n+1)): for j in range((m+1)): if search(i,j)>maxi2: now=i,j maxi2=search(i,j) print(maxi+maxi2) except: break ''' ''' https://www.nowcoder.com/test/question/cee98a512ec246a2918ea8121f7612c8?pid=710847&tid=19243264 [编程题] 奖学金 时间限制:1秒 空间限制:32768K 小v今年有n门课,每门都有考试,为了拿到奖学金,小v必须让自己的平均成绩至少为avg。每门课由平时成绩和考试成绩组成,满分为r。现在他知道每门课的平时成绩为ai ,若想让这门课的考试成绩多拿一分的话,小v要花bi 的时间复习,不复习的话当然就是0分。同时我们显然可以发现复习得再多也不会拿到超过满分的分数。为了拿到奖学金,小v至少要花多少时间复习。 输入描述: 第一行三个整数n,r,avg(n大于等于1小于等于1e5,r大于等于1小于等于1e9,avg大于等于1小于等于1e6),接下来n行,每行两个整数ai和bi,均小于等于1e6大于等于1 输出描述: 一行输出答案。 输入例子1: 5 10 9 0 5 9 1 8 1 0 1 9 100 输出例子1: 43 应该是贪心法.从收益最高的开始学习 while 1: try: n,r,avg=map(int,input().split()) save=[] for i in range((n)): save.append([int(i)for i in input().split()][::-1]) needall=avg*n save.sort() now=0 for i in range(len(save)): now+=save[i][1] #print(now)#目前总分 study=0 for i in range(len(save)): if now<needall: if now+r-save[i][1]<=needall: study+=save[i][0]*(r-save[i][1]) now+=r-save[i][1] else: study+=save[i][0]*(needall-now) now+=needall-now else: break print(study) except: break ''' ''' https://www.nowcoder.com/question/next?pid=710847&qid=26023&tid=19243264 [编程题] 路灯 时间限制:1秒 空间限制:32768K ........................... 0 a1 a2 1 一条长l的笔直的街道上有n个路灯,若这条街的起点为0,终点为l,第i个路灯坐标为ai ,每盏灯可以覆盖到的最远距离为d,为了照明需求,所有灯的灯光必须覆盖整条街,但是为了省电,要使这个d最小,请找到这个最小的d。 输入描述: 每组数据第一行两个整数n和l(n大于0小于等于1000,l小于等于1000000000大于0)。第二行有n个整数(均大于等于0小于等于l),为每盏灯的坐标,多个路灯可以在同一点。 输出描述: 输出答案,保留两位小数。 输入例子1: 7 15 15 5 3 7 9 14 0 输出例子1: 2.50 排序后间距相邻的间距最远的两个灯的距离除以2即可. while 1: try: n,l=map(int,input().split()) arr=[int(i)for i in input().split()] arr.sort() maxi=0 for i in range(len(arr)-1): if arr[i+1]-arr[i]>maxi: maxi=arr[i+1]-arr[i] maxi=maxi/2 if 0 not in arr: first=arr[0]-0 maxi=max(maxi,first) if l not in arr: end=l-arr[-1] maxi=max(maxi,end) print('%.2f'%(maxi)) except: break ''' ''' [编程题] 牛牛找工作 时间限制:2秒 空间限制:65536K 为了找到自己满意的工作,牛牛收集了每种工作的难度和报酬。牛牛选工作的标准是在难度不超过自身能力值的情况下,牛牛选择报酬最高的工作。在牛牛选定了自己的工作后,牛牛的小伙伴们来找牛牛帮忙选工作,牛牛依然使用自己的标准来帮助小伙伴们。牛牛的小伙伴太多了,于是他只好把这个任务交给了你。 输入描述: 每个输入包含一个测试用例。 每个测试用例的第一行包含两个正整数,分别表示工作的数量N(N<=100000)和小伙伴的数量M(M<=100000)。 接下来的N行每行包含两个正整数,分别表示该项工作的难度Di(Di<=1000000000)和报酬Pi(Pi<=1000000000)。 接下来的一行包含M个正整数,分别表示M个小伙伴的能力值Ai(Ai<=1000000000)。 保证不存在两项工作的报酬相同。 输出描述: 对于每个小伙伴,在单独的一行输出一个正整数表示他能得到的最高报酬。一个工作可以被多个人选择。 输入例子1: 3 3 1 100 10 1000 1000000000 1001 9 10 1000000000 输出例子1: 100 1000 1001 1 把工作按照难度升序排列,然后数组的第二列是收入,收入里面如果有降序的就删除后面这一项. 用2分为每一个人找工作 ''' ''' [编程题] 被3整除 时间限制:1秒 空间限制:32768K 小Q得到一个神奇的数列: 1, 12, 123,...12345678910,1234567891011...。 数列是:0 1 1 0 1 1 011................. 显然是011循环的.所以根据r直接就能算1到r有多少个被3整除的数 并且小Q对于能否被3整除这个性质很感兴趣。 小Q现在希望你能帮他计算一下从数列的第l个到第r个(包含端点)有多少个数可以被3整除。 输入描述: 输入包括两个整数l和r(1 <= l <= r <= 1e9), 表示要求解的区间两端。 输出描述: 输出一个整数, 表示区间内能被3整除的数字个数。 输入例子1: 2 5 输出例子1: 3 例子说明1: 12, 123, 1234, 12345... 其中12, 123, 12345能被3整除。 l,r =map(int,input().split()) left=r %3 if left==1: left=0 if left==2: left=1 daor=r//3*2+left left=(l-1) %3 if left==1: left=0 if left==2: left=1 daol=(l-1)//3*2+left print(daor-daol) ''' ''' [编程题] 安置路灯 时间限制:1秒 空间限制:32768K 小Q正在给一条长度为n的道路设计路灯安置方案。 为了让问题更简单,小Q把道路视为n个方格,需要照亮的地方用'.'表示, 不需要照亮的障碍物格子用'X'表示。 小Q现在要在道路上设置一些路灯, 对于安置在pos位置的路灯, 这盏路灯可以照亮pos - 1, pos, pos + 1这三个位置。 小Q希望能安置尽量少的路灯照亮所有'.'区域, 希望你能帮他计算一下最少需要多少盏路灯。 输入描述: 输入的第一行包含一个正整数t(1 <= t <= 1000), 表示测试用例数 接下来每两行一个测试数据, 第一行一个正整数n(1 <= n <= 1000),表示道路的长度。 第二行一个字符串s表示道路的构造,只包含'.'和'X'。 输出描述: 对于每个测试用例, 输出一个正整数表示最少需要多少盏路灯。 输入例子1: 2 3 .X. 11 ...XX....XX 输出例子1: 1 3 算法:遇到.就用一个灯放在这个.的后面.所以当前位置就+3 遇到x就不放灯,直接位置+1.不好说清楚为什么这么放最少. n=int(input()) for i in range((n)): chang=int(input()) lu=input() dex=0 count=0 while dex<len(lu): if lu[dex]=='.': count+=1 dex+=3 else: dex+=1 print(count) ''' ''' [编程题] 迷路的牛牛 时间限制:1秒 空间限制:32768K 牛牛去犇犇老师家补课,出门的时候面向北方,但是现在他迷路了。虽然他手里有一张地图,但是他需要知道自己面向哪个方向,请你帮帮他。 输入描述: 每个输入包含一个测试用例。 每个测试用例的第一行包含一个正整数,表示转方向的次数N(N<=1000)。 接下来的一行包含一个长度为N的字符串,由L和R组成,L表示向左转,R表示向右转。 输出描述: 输出牛牛最后面向的方向,N表示北,S表示南,E表示东,W表示西。 输入例子1: 3 LRR 输出例子1: E n=int(input()) a=input() arr='NESW' count=0 for i in range(len(a)): if a[i]=='L': count-=1 else: count+=1 count=(count+4*abs(count))%4 print(arr[count]) ''' ''' [编程题] 数对 时间限制:1秒 空间限制:32768K 牛牛以前在老师那里得到了一个正整数数对(x, y), 牛牛忘记他们具体是多少了。 但是牛牛记得老师告诉过他x和y均不大于n, 并且x除以y的余数大于等于k。 牛牛希望你能帮他计算一共有多少个可能的数对。 输入描述: 输入包括两个正整数n,k(1 <= n <= 10^5, 0 <= k <= n - 1)。 输出描述: 对于每个测试用例, 输出一个正整数表示可能的数对数量。 输入例子1: 5 2 5 3 y一定大于k (3,4) (3,5) (4,5) 输出例子1: 7 例子说明1: 满足条件的数对有(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),(5,3) Python3(3.5.2)重置自测 1 不会: 答案: def find_pairs(): n, k = map(int, raw_input().split()) cnt = 0 if k == 0: return pow(n, 2) for i in range(k + 1, n+1): //表示每i个数会出现一些需要的数,最后加上尾巴即可. cnt += n // i * (i - k) + (n % i - k + 1 if n % i >= k else 0) return cnt print find_pairs() ''' ''' https://www.nowcoder.com/question/next?pid=9763997&qid=152612&tid=19266166 [编程题] 矩形重叠 时间限制:1秒 空间限制:32768K 平面内有n个矩形, 第i个矩形的左下角坐标为(x1[i], y1[i]), 右上角坐标为(x2[i], y2[i])。 如果两个或者多个矩形有公共区域则认为它们是相互重叠的(不考虑边界和角落)。 请你计算出平面内重叠矩形数量最多的地方,有多少个矩形相互重叠。 输入描述: 输入包括五行。 第一行包括一个整数n(2 <= n <= 50), 表示矩形的个数。 第二行包括n个整数x1[i](-10^9 <= x1[i] <= 10^9),表示左下角的横坐标。 第三行包括n个整数y1[i](-10^9 <= y1[i] <= 10^9),表示左下角的纵坐标。 第四行包括n个整数x2[i](-10^9 <= x2[i] <= 10^9),表示右上角的横坐标。 第五行包括n个整数y2[i](-10^9 <= y2[i] <= 10^9),表示右上角的纵坐标。 输出描述: 输出一个正整数, 表示最多的地方有多少个矩形相互重叠,如果矩形都不互相重叠,输出1。 输入例子1: 2 0 90 0 90 100 200 100 200 输出例子1: 2 把每一个矩阵的4个边都看成4条无限长直线. 最后需要的区域一定是被4条直线加起来的区域. 别人答案: import sys lines = sys.stdin.readlines() n = int(lines[0]) x1 = list(map(int,lines[1].split())) y1 = list(map(int,lines[2].split())) x2 = list(map(int,lines[3].split())) y2 = list(map(int,lines[4].split())) res = 1 for x in x1+x2:#所有的横坐标切分点 for y in y1+y2:#所有的纵坐标切分店 cnt = 0 for i in range(n): #在所有的横纵切分点里面,如果这个切分点在当前矩阵在内部就让这个切分点的cnt+1 if x > x1[i] and y > y1[i] and x <= x2[i] and y <= y2[i]: cnt += 1 res = max(res,cnt) print(res) 或者: import sys lines = sys.stdin.readlines() n = int(lines[0]) x1 = list(map(int,lines[1].split())) y1 = list(map(int,lines[2].split())) x2 = list(map(int,lines[3].split())) y2 = list(map(int,lines[4].split())) res = 1 for x in x1+x2:#所有的横坐标切分点 for y in y1+y2:#所有的纵坐标切分店 cnt = 0 for i in range(n): #在所有的横纵切分点里面,如果这个切分点在当前矩阵在内部就让这个切分点的cnt+1 #就是下面的判定需要一个是大于等于一个是小于也可以.就是保证矩阵相交点,边时候不算相交 if x >= x1[i] and y >= y1[i] and x <x2[i] and y < y2[i]: cnt += 1 res = max(res,cnt) print(res) ''' ''' [编程题] 牛牛的背包问题 时间限制:1秒 空间限制:32768K 牛牛准备参加学校组织的春游, 出发前牛牛准备往背包里装入一些零食, 牛牛的背包容量为w。 牛牛家里一共有n袋零食, 第i袋零食体积为v[i]。 牛牛想知道在总体积不超过背包容量的情况下,他一共有多少种零食放法(总体积为0也算一种放法)。 输入描述: 输入包括两行 第一行为两个正整数n和w(1 <= n <= 30, 1 <= w <= 2 * 10^9),表示零食的数量和背包的容量。 第二行n个正整数v[i](0 <= v[i] <= 10^9),表示每袋零食的体积。 输出描述: 输出一个正整数, 表示牛牛一共有多少种零食放法。 输入例子1: 3 10 1 2 4 输出例子1: 8 例子说明1: 三种零食总体积小于10,于是每种零食有放入和不放入两种情况,一共有2*2*2 = 8种情况。 n,w=map(int,input().split()) arr=[int(i)for i in input().split()] def cnt(arr,w): if arr==[]: return 1 if arr[0]<=w: tmp=arr[:] tmp.pop(0) return cnt(tmp,w)+cnt(tmp,w-arr[0]) if arr[0]>w: tmp=arr[:] tmp.pop(0) return cnt(tmp,w) if sum(arr)<=m:#这个题目需要用这个公式来加速 print(2**len(arr)) else: print(cnt(arr,w)) 别人代码:写的逼我简介,主要是空间消耗逼我的少,看这个改我的上面代码 line = raw_input() n = int(line.split(' ')[0]) w = int(line.split(' ')[1]) line = raw_input() v = [] for i in range(n): v.append(int(line.strip().split(' ')[i])) ans = 0 def main(v, w): global ans if sum(v) <= w: print 2**(len(v)) else: v.sort() dfs(0, 0) print ans def dfs(su, loc):#看这个是怎么设计的递归函数 #这个函数第一个是目前的重量,第二个是当前在v中的index global ans if su > w: return if su <= w: ans += 1 for i in range(loc, n):#表示如果当前重量没超过w,那么嗨可以继续放后面index中的一个.继续判断 #这个递归函数写的,充分避免了数组的使用和数组重复的复制,只用下表就表示了数组的变化 dfs(su+v[i], i+1) main(v, w) ''' ''' https://www.nowcoder.com/test/question/32c71b52db52424c89a565e4134bfe4e?pid=6910869&tid=19267265 [编程题] 魔法币 时间限制:1秒 空间限制:32768K 小易准备去魔法王国采购魔法神器,购买魔法神器需要使用魔法币,但是小易现在一枚魔法币都没有,但是小易有两台魔法机器可以通过投入x(x可以为0)个魔法币产生更多的魔法币。 魔法机器1:如果投入x个魔法币,魔法机器会将其变为2x+1个魔法币 魔法机器2:如果投入x个魔法币,魔法机器会将其变为2x+2个魔法币 小易采购魔法神器总共需要n个魔法币,所以小易只能通过两台魔法机器产生恰好n个魔法币,小易需要你帮他设计一个投入方案使他最后恰好拥有n个魔法币。 输入描述: 输入包括一行,包括一个正整数n(1 ≤ n ≤ 10^9),表示小易需要的魔法币数量。 输出描述: 输出一个字符串,每个字符表示该次小易选取投入的魔法机器。其中只包含字符'1'和'2'。 输入例子1: 输出例子1: 122 分析知道,第一个机器出来的一定是奇数 第二个机器出来的一定是偶数.所以根据最后需要的硬币,倒着推即可 a=int(input()) ans='' while a!=0: if a%2==0: ans+='2' a=(a-2)//2 else: ans+='1' a=(a-1)//2 print(ans[::-1]) ''' ''' [编程题] 相反数 时间限制:1秒 空间限制:32768K 为了得到一个数的"相反数",我们将这个数的数字顺序颠倒,然后再加上原先的数得到"相反数"。例如,为了得到1325的"相反数",首先我们将该数的数字顺序颠倒,我们得到5231,之后再加上原先的数,我们得到5231+1325=6556.如果颠倒之后的数字有前缀零,前缀零将会被忽略。例如n = 100, 颠倒之后是1. 输入描述: 输入包括一个整数n,(1 ≤ n ≤ 10^5) 输出描述: 输出一个整数,表示n的相反数 输入例子1: 1325 输出例子1: 6556 a=int(input()) print(a+int(str(a)[::-1])) ''' ''' [编程题] 字符串碎片 时间限制:1秒 空间限制:32768K 一个由小写字母组成的字符串可以看成一些同一字母的最大碎片组成的。例如,"aaabbaaac"是由下面碎片组成的:'aaa','bb','c'。牛牛现在给定一个字符串,请你帮助计算这个字符串的所有碎片的平均长度是多少。 输入描述: 输入包括一个字符串s,字符串s的长度length(1 ≤ length ≤ 50),s只含小写字母('a'-'z') 输出描述: 输出一个整数,表示所有碎片的平均长度,四舍五入保留两位小数。 如样例所示: s = "aaabbaaac" 所有碎片的平均长度 = (3 + 2 + 3 + 1) / 4 = 2.25 输入例子1: aaabbaaac 输出例子1: 2.25 a=input() cnt=[] first=0 for i in range(1,len(a)): if a[i]!=a[i-1]: cnt.append(i-first) first=i cnt.append(len(a)-first) print('%.2f'%(sum(cnt)/len(cnt))) ''' ''' https://www.nowcoder.com/question/next?pid=6910869&qid=126950&tid=19267265 [编程题] 游历魔法王国 时间限制:1秒 空间限制:32768K 魔法王国一共有n个城市,编号为0~n-1号,n个城市之间的道路连接起来恰好构成一棵树。 小易现在在0号城市,每次行动小易会从当前所在的城市走到与其相邻的一个城市,小易最多能行动L次。 如果小易到达过某个城市就视为小易游历过这个城市了,小易现在要制定好的旅游计划使他能游历最多的城市,请你帮他计算一下他最多能游历过多少个城市(注意0号城市已经游历了,游历过的城市不重复计算)。 输入描述: 输入包括两行,第一行包括两个正整数n(2 ≤ n ≤ 50)和L(1 ≤ L ≤ 100),表示城市个数和小易能行动的次数。 第二行包括n-1个整数parent[i](0 ≤ parent[i] ≤ i), 对于每个合法的i(0 ≤ i ≤ n - 2),在(i+1)号城市和parent[i]间有一条道路连接。 输出描述: 输出一个整数,表示小易最多能游历的城市数量。 输入例子1: 5 2 0 1 2 3 输出例子1: 3 '''
这个总结挺好:
LSTM 和GRU的区别
先给出一些结论:
- GRU和LSTM的性能在很多任务上不分伯仲。
- GRU 参数更少因此更容易收敛,但是数据集很大的情况下,LSTM表达性能更好。
- 从结构上来说,GRU只有两个门(update和reset),LSTM有三个门(forget,input,output),GRU直接将hidden state 传给下一个单元,而LSTM则用memory cell 把hidden state 包装起来。
1. 基本结构
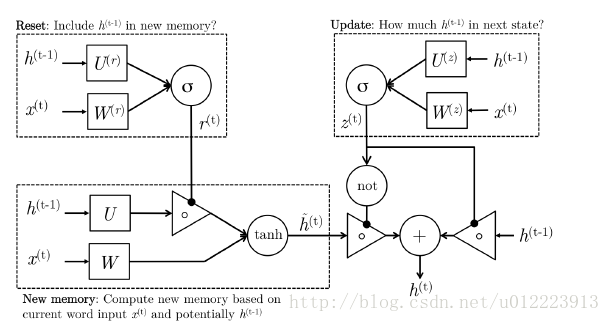
1.1 GRU
GRU的设计是为了更好的捕捉long-term dependencies。我们先来看看输入ht−1ht−1和x(t)x(t), GRU怎么通过计算输出h(t)h(t):
-
Reset gate
r(t)r(t) 负责决定h(t−1)h(t−1) 对new memory h^(t)h^(t) 的重要性有多大, 如果r(t)r(t) 约等于0 的话,h(t−1)h(t−1) 就不会传递给new memory h^(t)h^(t)
-
new memory
h^(t)h^(t) 是对新的输入x(t)x(t) 和上一时刻的hidden state h(t−1)h(t−1) 的总结。计算总结出的新的向量h^(t)h^(t) 包含上文信息和新的输入x(t)x(t).
-
Update gate
z(t)z(t) 负责决定传递多少ht−1ht−1给htht 。 如果z(t)z(t) 约等于1的话,ht−1ht−1 几乎会直接复制给htht ,相反,如果z(t)z(t) 约等于0, new memory h^(t)h^(t) 直接传递给htht.
-
Hidden state:
h(t)h(t) 由 h(t−1)h(t−1) 和h^(t)h^(t) 相加得到,两者的权重由update gate z(t)z(t) 控制。
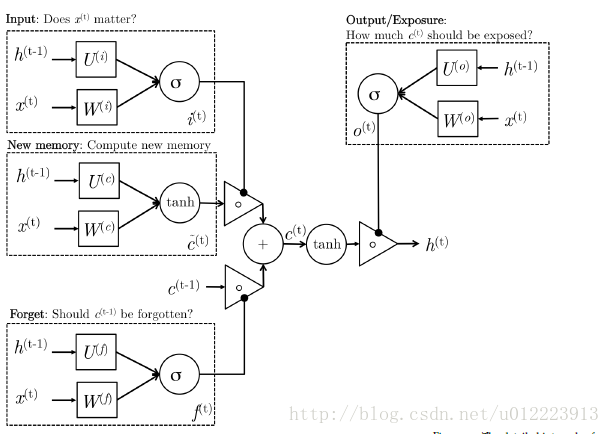
1.2 LSTM
LSTM 的设计也是为了更好的捕捉long-term dependencies,但是结构上有一些不同,更复杂一些,我们想来看看计算过程:
-
new memory cell
这一步和GRU中的new memory类似,输出的向量c^(t)c^(t)都是对新的输入x(t)x(t) 和上一时刻的hidden state h(t−1)h(t−1) 的总结。
-
Input gate
i(t)i(t)负责决定输入的x(t)x(t) 信息是否值得保存。
-
Forget gate
f(t)f(t)负责决定past memory cell c^(t−1)c^(t−1)对c(t)c(t) 的重要性。
-
final memory cell
c(t)c(t) 由c^(t−1)c^(t−1) 和c^(t)c^(t) 相加得到,权重分别由 Forget gate 和Input gate 决定
-
Output gate
这个门是GRU没有的。它负责决定c(t)c(t) 中的哪些部分应该传递给hidden state h(t)h(t)
2. 区别
1. 对memory 的控制
LSTM: 用output gate 控制,传输给下一个unit
GRU:直接传递给下一个unit,不做任何控制
2. input gate 和reset gate 作用位置不同
LSTM: 计算new memory c^(t)c^(t)时 不对上一时刻的信息做任何控制,而是用forget gate 独立的实现这一点
GRU: 计算new memory h^(t)h^(t) 时利用reset gate 对上一时刻的信息 进行控制。
3. 相似
最大的相似之处就是, 在从t 到 t-1 的更新时都引入了加法。
这个加法的好处在于能防止梯度弥散,因此LSTM和GRU都比一般的RNN效果更好。
交叉熵的推导
https://blog.csdn.net/red_stone1/article/details/80735068
保存一波

#下面这一段用一个txt来保存input的信息来模拟input.最后提交代码时候删除这一段即可. a9999=open('1.txt','r') def input(): return a9999.readline().rstrip(' ') #输入数据的一些模板 # n,a=map(int,input().split()) # arr=[int(i)for i in input().split()] # 格式化输出 # print('%.2f'%(maxi/2)) ''' # 最大公约数用 import fractions fractions.gcd(a,b) ''' ''' [编程题] 小易的升级之路 时间限制:1秒 空间限制:32768K #小易经常沉迷于网络游戏.有一次,他在玩一个打怪升级的游戏,他的角色的初始能力值为 a.在接下来的一段时间内,他将会依次遇见n个怪物,每个怪物的防御力为b1,b2,b3...bn. 如果遇到的怪物防御力bi小于等于小易的当前能力值c,那么他就能轻松打败怪物,并 且使得自己的能力值增加bi;如果bi大于c,那他也能打败怪物,但他的能力值只能增加bi 与c的最大公约数.那么问题来了,在一系列的锻炼后,小易的最终能力值为多少? 输入描述: 对于每组数据,第一行是两个整数n(1≤n<100000)表示怪物的数量和a表示小易的初始能力值. 第二行n个整数,b1,b2...bn(1≤bi≤n)表示每个怪物的防御力 import fractions while 1:#处理多段不知道多少的输入用这个方法死循环+内层try except break套路 try: now=input() if now=='': break n,a=map(int,now.split()) for i in range((n)): b=int(input()) if b<=a: a+=b else: a+=fractions.gcd(a,b) print(a) except: break ''' ''' [编程题] 炮台攻击 时间限制:1秒 空间限制:32768K 兰博教训提莫之后,然后和提莫讨论起约德尔人,谈起约德尔人,自然少不了一个人,那 就是黑默丁格------约德尔人历史上最伟大的科学家. 提莫说,黑默丁格最近在思考一个问题:黑默丁格有三个炮台,炮台能攻击到距离它R的敌人 (两点之间的距离为两点连续的距离,例如(3,0),(0,4)之间的距离是5),如果一个炮台能攻击 到敌人,那么就会对敌人造成1×的伤害.黑默丁格将三个炮台放在N*M方格中的点上,并且给出敌人 的坐标. 问:那么敌人受到伤害会是多大? 输入描述: 第一行9个整数,R,x1,y1,x2,y2,x3,y3,x0,y0.R代表炮台攻击的最大距离,(x1,y1),(x2,y2), (x3,y3)代表三个炮台的坐标.(x0,y0)代表敌人的坐标. 输出描述: 输出一行,这一行代表敌人承受的最大伤害,(如果每个炮台都不能攻击到敌人,输出0×) 输入例子1: 1 1 1 2 2 3 3 1 2 输出例子1: 2x while 1: try: r,x1,y1,x2,y2,x3,y3,x0,y0=map(int,input().split()) count=0 if ((x1-x0)**2+(y1-y0)**2)**0.5<=r: count+=1 if ((x2-x0)**2+(y2-y0)**2)**0.5<=r: count+=1 if ((x3-x0)**2+(y3-y0)**2)**0.5<=r: count+=1 print(str(count)+'x') except: break ''' ''' https://www.nowcoder.com/test/question/fe6c73cb899c4fe1bdd773f8d3b42c3d?pid=970447&tid=19242023 牛客网的网站有问题,搜索试卷是出不来的,只能按照连接点进去才行. [编程题] 扫描透镜 时间限制:1秒 空间限制:32768K 在N*M的草地上,提莫种了K个蘑菇,蘑菇爆炸的威力极大,兰博不想贸然去闯,而且蘑菇是隐形的.只 有一种叫做扫描透镜的物品可以扫描出隐形的蘑菇,于是他回了一趟战争学院,买了2个扫描透镜,一个 扫描透镜可以扫描出(3*3)方格中所有的蘑菇,然后兰博就可以清理掉一些隐形的蘑菇. 问:兰博最多可以清理多少个蘑菇? 注意:每个方格被扫描一次只能清除掉一个蘑菇。 输入描述: 第一行三个整数:N,M,K,(1≤N,M≤20,K≤100),N,M代表了草地的大小; 接下来K行,每行两个整数x,y(1≤x≤N,1≤y≤M).代表(x,y)处提莫种了一个蘑菇. 一个方格可以种无穷个蘑菇. 输出描述: 输出一行,在这一行输出一个整数,代表兰博最多可以清理多少个蘑菇. 扫描2次,每一次都找最多的那个3*3进行轰炸即可 地图问题都先加一圈边界,边界上炸弹设置数量为0 #这题目虽然简单,但学到了很多地图上的技巧 while 1: try: n,m,k=map(int,input().split()) save=[[0]*(m+2) for i in range(n+2)] for i in range((k)): a,b=map(int,input().split()) save[a][b]+=1 def search(i,j): #返回save上i,j位置3*3内有多少个地方有地雷 count=0 #先把转移坐标写成列表 arr=[(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1)] for _ in range(len(arr)): newdex=i+arr[_][0],j+arr[_][1] if save[newdex[0]][newdex[1]]>0: count+=1 return count def jian(i,j): #清楚save上i,j位置3*3内每一个地方的一个地雷 #先把转移坐标写成列表 arr=[(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1)] for _ in range(len(arr)): newdex=i+arr[_][0],j+arr[_][1] if save[newdex[0]][newdex[1]]>0: save[newdex[0]][newdex[1]]-=1 #地图实际范围是从1到n 从1到m maxi=0 for i in range(1,(n+1)): for j in range(1,(m+1)): if search(i,j)>maxi: now=i,j maxi=search(i,j) jian(now[0],now[1]) maxi2=0 for i in range((n+1)): for j in range((m+1)): if search(i,j)>maxi2: now=i,j maxi2=search(i,j) print(maxi+maxi2) except: break ''' ''' https://www.nowcoder.com/test/question/cee98a512ec246a2918ea8121f7612c8?pid=710847&tid=19243264 [编程题] 奖学金 时间限制:1秒 空间限制:32768K 小v今年有n门课,每门都有考试,为了拿到奖学金,小v必须让自己的平均成绩至少为avg。每门课由平时成绩和考试成绩组成,满分为r。现在他知道每门课的平时成绩为ai ,若想让这门课的考试成绩多拿一分的话,小v要花bi 的时间复习,不复习的话当然就是0分。同时我们显然可以发现复习得再多也不会拿到超过满分的分数。为了拿到奖学金,小v至少要花多少时间复习。 输入描述: 第一行三个整数n,r,avg(n大于等于1小于等于1e5,r大于等于1小于等于1e9,avg大于等于1小于等于1e6),接下来n行,每行两个整数ai和bi,均小于等于1e6大于等于1 输出描述: 一行输出答案。 输入例子1: 5 10 9 0 5 9 1 8 1 0 1 9 100 输出例子1: 43 应该是贪心法.从收益最高的开始学习 while 1: try: n,r,avg=map(int,input().split()) save=[] for i in range((n)): save.append([int(i)for i in input().split()][::-1]) needall=avg*n save.sort() now=0 for i in range(len(save)): now+=save[i][1] #print(now)#目前总分 study=0 for i in range(len(save)): if now<needall: if now+r-save[i][1]<=needall: study+=save[i][0]*(r-save[i][1]) now+=r-save[i][1] else: study+=save[i][0]*(needall-now) now+=needall-now else: break print(study) except: break ''' ''' https://www.nowcoder.com/question/next?pid=710847&qid=26023&tid=19243264 [编程题] 路灯 时间限制:1秒 空间限制:32768K ........................... 0 a1 a2 1 一条长l的笔直的街道上有n个路灯,若这条街的起点为0,终点为l,第i个路灯坐标为ai ,每盏灯可以覆盖到的最远距离为d,为了照明需求,所有灯的灯光必须覆盖整条街,但是为了省电,要使这个d最小,请找到这个最小的d。 输入描述: 每组数据第一行两个整数n和l(n大于0小于等于1000,l小于等于1000000000大于0)。第二行有n个整数(均大于等于0小于等于l),为每盏灯的坐标,多个路灯可以在同一点。 输出描述: 输出答案,保留两位小数。 输入例子1: 7 15 15 5 3 7 9 14 0 输出例子1: 2.50 排序后间距相邻的间距最远的两个灯的距离除以2即可. while 1: try: n,l=map(int,input().split()) arr=[int(i)for i in input().split()] arr.sort() maxi=0 for i in range(len(arr)-1): if arr[i+1]-arr[i]>maxi: maxi=arr[i+1]-arr[i] maxi=maxi/2 if 0 not in arr: first=arr[0]-0 maxi=max(maxi,first) if l not in arr: end=l-arr[-1] maxi=max(maxi,end) print('%.2f'%(maxi)) except: break ''' ''' [编程题] 牛牛找工作 时间限制:2秒 空间限制:65536K 为了找到自己满意的工作,牛牛收集了每种工作的难度和报酬。牛牛选工作的标准是在难度不超过自身能力值的情况下,牛牛选择报酬最高的工作。在牛牛选定了自己的工作后,牛牛的小伙伴们来找牛牛帮忙选工作,牛牛依然使用自己的标准来帮助小伙伴们。牛牛的小伙伴太多了,于是他只好把这个任务交给了你。 输入描述: 每个输入包含一个测试用例。 每个测试用例的第一行包含两个正整数,分别表示工作的数量N(N<=100000)和小伙伴的数量M(M<=100000)。 接下来的N行每行包含两个正整数,分别表示该项工作的难度Di(Di<=1000000000)和报酬Pi(Pi<=1000000000)。 接下来的一行包含M个正整数,分别表示M个小伙伴的能力值Ai(Ai<=1000000000)。 保证不存在两项工作的报酬相同。 输出描述: 对于每个小伙伴,在单独的一行输出一个正整数表示他能得到的最高报酬。一个工作可以被多个人选择。 输入例子1: 3 3 1 100 10 1000 1000000000 1001 9 10 1000000000 输出例子1: 100 1000 1001 1 把工作按照难度升序排列,然后数组的第二列是收入,收入里面如果有降序的就删除后面这一项. 用2分为每一个人找工作 ''' ''' [编程题] 被3整除 时间限制:1秒 空间限制:32768K 小Q得到一个神奇的数列: 1, 12, 123,...12345678910,1234567891011...。 数列是:0 1 1 0 1 1 011................. 显然是011循环的.所以根据r直接就能算1到r有多少个被3整除的数 并且小Q对于能否被3整除这个性质很感兴趣。 小Q现在希望你能帮他计算一下从数列的第l个到第r个(包含端点)有多少个数可以被3整除。 输入描述: 输入包括两个整数l和r(1 <= l <= r <= 1e9), 表示要求解的区间两端。 输出描述: 输出一个整数, 表示区间内能被3整除的数字个数。 输入例子1: 2 5 输出例子1: 3 例子说明1: 12, 123, 1234, 12345... 其中12, 123, 12345能被3整除。 l,r =map(int,input().split()) left=r %3 if left==1: left=0 if left==2: left=1 daor=r//3*2+left left=(l-1) %3 if left==1: left=0 if left==2: left=1 daol=(l-1)//3*2+left print(daor-daol) ''' ''' [编程题] 安置路灯 时间限制:1秒 空间限制:32768K 小Q正在给一条长度为n的道路设计路灯安置方案。 为了让问题更简单,小Q把道路视为n个方格,需要照亮的地方用'.'表示, 不需要照亮的障碍物格子用'X'表示。 小Q现在要在道路上设置一些路灯, 对于安置在pos位置的路灯, 这盏路灯可以照亮pos - 1, pos, pos + 1这三个位置。 小Q希望能安置尽量少的路灯照亮所有'.'区域, 希望你能帮他计算一下最少需要多少盏路灯。 输入描述: 输入的第一行包含一个正整数t(1 <= t <= 1000), 表示测试用例数 接下来每两行一个测试数据, 第一行一个正整数n(1 <= n <= 1000),表示道路的长度。 第二行一个字符串s表示道路的构造,只包含'.'和'X'。 输出描述: 对于每个测试用例, 输出一个正整数表示最少需要多少盏路灯。 输入例子1: 2 3 .X. 11 ...XX....XX 输出例子1: 1 3 算法:遇到.就用一个灯放在这个.的后面.所以当前位置就+3 遇到x就不放灯,直接位置+1.不好说清楚为什么这么放最少. n=int(input()) for i in range((n)): chang=int(input()) lu=input() dex=0 count=0 while dex<len(lu): if lu[dex]=='.': count+=1 dex+=3 else: dex+=1 print(count) ''' ''' [编程题] 迷路的牛牛 时间限制:1秒 空间限制:32768K 牛牛去犇犇老师家补课,出门的时候面向北方,但是现在他迷路了。虽然他手里有一张地图,但是他需要知道自己面向哪个方向,请你帮帮他。 输入描述: 每个输入包含一个测试用例。 每个测试用例的第一行包含一个正整数,表示转方向的次数N(N<=1000)。 接下来的一行包含一个长度为N的字符串,由L和R组成,L表示向左转,R表示向右转。 输出描述: 输出牛牛最后面向的方向,N表示北,S表示南,E表示东,W表示西。 输入例子1: 3 LRR 输出例子1: E n=int(input()) a=input() arr='NESW' count=0 for i in range(len(a)): if a[i]=='L': count-=1 else: count+=1 count=(count+4*abs(count))%4 print(arr[count]) ''' ''' [编程题] 数对 时间限制:1秒 空间限制:32768K 牛牛以前在老师那里得到了一个正整数数对(x, y), 牛牛忘记他们具体是多少了。 但是牛牛记得老师告诉过他x和y均不大于n, 并且x除以y的余数大于等于k。 牛牛希望你能帮他计算一共有多少个可能的数对。 输入描述: 输入包括两个正整数n,k(1 <= n <= 10^5, 0 <= k <= n - 1)。 输出描述: 对于每个测试用例, 输出一个正整数表示可能的数对数量。 输入例子1: 5 2 5 3 y一定大于k (3,4) (3,5) (4,5) 输出例子1: 7 例子说明1: 满足条件的数对有(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),(5,3) Python3(3.5.2)重置自测 1 不会: 答案: def find_pairs(): n, k = map(int, raw_input().split()) cnt = 0 if k == 0: return pow(n, 2) for i in range(k + 1, n+1): //表示每i个数会出现一些需要的数,最后加上尾巴即可. cnt += n // i * (i - k) + (n % i - k + 1 if n % i >= k else 0) return cnt print find_pairs() ''' ''' https://www.nowcoder.com/question/next?pid=9763997&qid=152612&tid=19266166 [编程题] 矩形重叠 时间限制:1秒 空间限制:32768K 平面内有n个矩形, 第i个矩形的左下角坐标为(x1[i], y1[i]), 右上角坐标为(x2[i], y2[i])。 如果两个或者多个矩形有公共区域则认为它们是相互重叠的(不考虑边界和角落)。 请你计算出平面内重叠矩形数量最多的地方,有多少个矩形相互重叠。 输入描述: 输入包括五行。 第一行包括一个整数n(2 <= n <= 50), 表示矩形的个数。 第二行包括n个整数x1[i](-10^9 <= x1[i] <= 10^9),表示左下角的横坐标。 第三行包括n个整数y1[i](-10^9 <= y1[i] <= 10^9),表示左下角的纵坐标。 第四行包括n个整数x2[i](-10^9 <= x2[i] <= 10^9),表示右上角的横坐标。 第五行包括n个整数y2[i](-10^9 <= y2[i] <= 10^9),表示右上角的纵坐标。 输出描述: 输出一个正整数, 表示最多的地方有多少个矩形相互重叠,如果矩形都不互相重叠,输出1。 输入例子1: 2 0 90 0 90 100 200 100 200 输出例子1: 2 把每一个矩阵的4个边都看成4条无限长直线. 最后需要的区域一定是被4条直线加起来的区域. 别人答案: import sys lines = sys.stdin.readlines() n = int(lines[0]) x1 = list(map(int,lines[1].split())) y1 = list(map(int,lines[2].split())) x2 = list(map(int,lines[3].split())) y2 = list(map(int,lines[4].split())) res = 1 for x in x1+x2:#所有的横坐标切分点 for y in y1+y2:#所有的纵坐标切分店 cnt = 0 for i in range(n): #在所有的横纵切分点里面,如果这个切分点在当前矩阵在内部就让这个切分点的cnt+1 if x > x1[i] and y > y1[i] and x <= x2[i] and y <= y2[i]: cnt += 1 res = max(res,cnt) print(res) 或者: import sys lines = sys.stdin.readlines() n = int(lines[0]) x1 = list(map(int,lines[1].split())) y1 = list(map(int,lines[2].split())) x2 = list(map(int,lines[3].split())) y2 = list(map(int,lines[4].split())) res = 1 for x in x1+x2:#所有的横坐标切分点 for y in y1+y2:#所有的纵坐标切分店 cnt = 0 for i in range(n): #在所有的横纵切分点里面,如果这个切分点在当前矩阵在内部就让这个切分点的cnt+1 #就是下面的判定需要一个是大于等于一个是小于也可以.就是保证矩阵相交点,边时候不算相交 if x >= x1[i] and y >= y1[i] and x <x2[i] and y < y2[i]: cnt += 1 res = max(res,cnt) print(res) ''' ''' [编程题] 牛牛的背包问题 时间限制:1秒 空间限制:32768K 牛牛准备参加学校组织的春游, 出发前牛牛准备往背包里装入一些零食, 牛牛的背包容量为w。 牛牛家里一共有n袋零食, 第i袋零食体积为v[i]。 牛牛想知道在总体积不超过背包容量的情况下,他一共有多少种零食放法(总体积为0也算一种放法)。 输入描述: 输入包括两行 第一行为两个正整数n和w(1 <= n <= 30, 1 <= w <= 2 * 10^9),表示零食的数量和背包的容量。 第二行n个正整数v[i](0 <= v[i] <= 10^9),表示每袋零食的体积。 输出描述: 输出一个正整数, 表示牛牛一共有多少种零食放法。 输入例子1: 3 10 1 2 4 输出例子1: 8 例子说明1: 三种零食总体积小于10,于是每种零食有放入和不放入两种情况,一共有2*2*2 = 8种情况。 n,w=map(int,input().split()) arr=[int(i)for i in input().split()] def cnt(arr,w): if arr==[]: return 1 if arr[0]<=w: tmp=arr[:] tmp.pop(0) return cnt(tmp,w)+cnt(tmp,w-arr[0]) if arr[0]>w: tmp=arr[:] tmp.pop(0) return cnt(tmp,w) if sum(arr)<=m:#这个题目需要用这个公式来加速 print(2**len(arr)) else: print(cnt(arr,w)) 别人代码:写的逼我简介,主要是空间消耗逼我的少,看这个改我的上面代码 line = raw_input() n = int(line.split(' ')[0]) w = int(line.split(' ')[1]) line = raw_input() v = [] for i in range(n): v.append(int(line.strip().split(' ')[i])) ans = 0 def main(v, w): global ans if sum(v) <= w: print 2**(len(v)) else: v.sort() dfs(0, 0) print ans def dfs(su, loc):#看这个是怎么设计的递归函数 #这个函数第一个是目前的重量,第二个是当前在v中的index global ans if su > w: return if su <= w: ans += 1 for i in range(loc, n):#表示如果当前重量没超过w,那么嗨可以继续放后面index中的一个.继续判断 #这个递归函数写的,充分避免了数组的使用和数组重复的复制,只用下表就表示了数组的变化 dfs(su+v[i], i+1) main(v, w) ''' ''' https://www.nowcoder.com/test/question/32c71b52db52424c89a565e4134bfe4e?pid=6910869&tid=19267265 [编程题] 魔法币 时间限制:1秒 空间限制:32768K 小易准备去魔法王国采购魔法神器,购买魔法神器需要使用魔法币,但是小易现在一枚魔法币都没有,但是小易有两台魔法机器可以通过投入x(x可以为0)个魔法币产生更多的魔法币。 魔法机器1:如果投入x个魔法币,魔法机器会将其变为2x+1个魔法币 魔法机器2:如果投入x个魔法币,魔法机器会将其变为2x+2个魔法币 小易采购魔法神器总共需要n个魔法币,所以小易只能通过两台魔法机器产生恰好n个魔法币,小易需要你帮他设计一个投入方案使他最后恰好拥有n个魔法币。 输入描述: 输入包括一行,包括一个正整数n(1 ≤ n ≤ 10^9),表示小易需要的魔法币数量。 输出描述: 输出一个字符串,每个字符表示该次小易选取投入的魔法机器。其中只包含字符'1'和'2'。 输入例子1: 输出例子1: 122 分析知道,第一个机器出来的一定是奇数 第二个机器出来的一定是偶数.所以根据最后需要的硬币,倒着推即可 a=int(input()) ans='' while a!=0: if a%2==0: ans+='2' a=(a-2)//2 else: ans+='1' a=(a-1)//2 print(ans[::-1]) ''' ''' [编程题] 相反数 时间限制:1秒 空间限制:32768K 为了得到一个数的"相反数",我们将这个数的数字顺序颠倒,然后再加上原先的数得到"相反数"。例如,为了得到1325的"相反数",首先我们将该数的数字顺序颠倒,我们得到5231,之后再加上原先的数,我们得到5231+1325=6556.如果颠倒之后的数字有前缀零,前缀零将会被忽略。例如n = 100, 颠倒之后是1. 输入描述: 输入包括一个整数n,(1 ≤ n ≤ 10^5) 输出描述: 输出一个整数,表示n的相反数 输入例子1: 1325 输出例子1: 6556 a=int(input()) print(a+int(str(a)[::-1])) ''' ''' [编程题] 字符串碎片 时间限制:1秒 空间限制:32768K 一个由小写字母组成的字符串可以看成一些同一字母的最大碎片组成的。例如,"aaabbaaac"是由下面碎片组成的:'aaa','bb','c'。牛牛现在给定一个字符串,请你帮助计算这个字符串的所有碎片的平均长度是多少。 输入描述: 输入包括一个字符串s,字符串s的长度length(1 ≤ length ≤ 50),s只含小写字母('a'-'z') 输出描述: 输出一个整数,表示所有碎片的平均长度,四舍五入保留两位小数。 如样例所示: s = "aaabbaaac" 所有碎片的平均长度 = (3 + 2 + 3 + 1) / 4 = 2.25 输入例子1: aaabbaaac 输出例子1: 2.25 a=input() cnt=[] first=0 for i in range(1,len(a)): if a[i]!=a[i-1]: cnt.append(i-first) first=i cnt.append(len(a)-first) print('%.2f'%(sum(cnt)/len(cnt))) ''' ''' https://www.nowcoder.com/question/next?pid=6910869&qid=126950&tid=19267265 [编程题] 游历魔法王国 时间限制:1秒 空间限制:32768K 魔法王国一共有n个城市,编号为0~n-1号,n个城市之间的道路连接起来恰好构成一棵树。 小易现在在0号城市,每次行动小易会从当前所在的城市走到与其相邻的一个城市,小易最多能行动L次。 如果小易到达过某个城市就视为小易游历过这个城市了,小易现在要制定好的旅游计划使他能游历最多的城市,请你帮他计算一下他最多能游历过多少个城市(注意0号城市已经游历了,游历过的城市不重复计算)。 输入描述:] 输入包括两行,第一行包括两个正整数n(2 ≤ n ≤ 50)和L(1 ≤ L ≤ 100),表示城市个数和小易能行动的次数。 第二行包括n-1个整数parent[i](0 ≤ parent[i] ≤ i), 对于每个合法的i(0 ≤ i ≤ n - 2),在(i+1)号城市和parent[i]间有一条道路连接。 #0 ≤ parent[i] ≤ i 注意这个条件,表示 i+1和parent[i]相连.并且parent[i]一定比i小. 输出描述: 输出一个整数,表示小易最多能游历的城市数量。 输入例子1: 5 2 0 1 2 3 输出例子1: 3 应该是dfs,bfs的题目.然而并不是 n,L=map(int,input().split()) arr=[int(i)for i in input().split()] dp=[0]*n dp[0]=1 for i in range(len(arr)): dp[i+1]=dp[arr[i]]+1 maxi=max(dp) if maxi-1<=L: print(maxi+(L-maxi+1)//2) else: print(L+1) ''' ''' [编程题] 重排数列 时间限制:1秒 空间限制:100768K 小易有一个长度为N的正整数数列A = {A[1], A[2], A[3]..., A[N]}。 牛博士给小易出了一个难题: 对数列A进行重新排列,使数列A满足所有的A[i] * A[i + 1](1 ≤ i ≤ N - 1)都是4的倍数。 小易现在需要判断一个数列是否可以重排之后满足牛博士的要求。 输入描述: 输入的第一行为数列的个数t(1 ≤ t ≤ 10), 接下来每两行描述一个数列A,第一行为数列长度n(1 ≤ n ≤ 10^5) 第二行为n个正整数A[i](1 ≤ A[i] ≤ 10^9) 输出描述: 对于每个数列输出一行表示是否可以满足牛博士要求,如果可以输出Yes,否则输出No。 输入例子1: 2 3 1 10 100 4 1 2 3 4 输出例子1: Yes No #看arr整体有多少个2的倍数和4的倍数 a=int(input()) for _ in range(a): chang=int(input()) arr=[int(i)for i in input().split()] cnt2=0 cnt4=0 for i in range(len(arr)): if arr[i]%4==0: cnt4+=1 continue if arr[i]%2==0: cnt2+=1 #分类:如果cnt2>0 and cnt4>0那么2的先紧致排一起,然后放一个4,再放一个奇数循环下去. if cnt2>0 and cnt4>0: tmp=cnt2+cnt4*2 k=(tmp>=len(arr)) elif cnt2==0 and cnt4>0: k=(cnt4>=len(arr)//2) elif cnt2>0 and cnt4==0: k=(cnt2>=len(arr)) else: k=(False) if k: print('Yes') #注意这个题目输出是yes,不是True...卡了我很久 else: print('No') ''' ''' #sublime的红波浪线用F6就能去掉. [编程题] 最长公共子括号序列 时间限制:1秒 空间限制:100768K 一个合法的括号匹配序列被定义为: 1. 空串""是合法的括号序列 2. 如果"X"和"Y"是合法的序列,那么"XY"也是一个合法的括号序列 3. 如果"X"是一个合法的序列,那么"(X)"也是一个合法的括号序列 4. 每个合法的括号序列都可以由上面的规则生成 例如"", "()", "()()()", "(()())", "(((()))"都是合法的。 从一个字符串S中移除零个或者多个字符得到的序列称为S的子序列。 例如"abcde"的子序列有"abe","","abcde"等。 定义LCS(S,T)为字符串S和字符串T最长公共子序列的长度,即一个最长的序列W既是S的子序列也是T的子序列的长度。 小易给出一个合法的括号匹配序列s,小易希望你能找出具有以下特征的括号序列t: 1、t跟s不同,但是长度相同 2、t也是一个合法的括号匹配序列 3、LCS(s, t)是满足上述两个条件的t中最大的 因为这样的t可能存在多个,小易需要你计算出满足条件的t有多少个。 如样例所示: s = "(())()",跟字符串s长度相同的合法括号匹配序列有: "()(())", "((()))", "()()()", "(()())",其中LCS( "(())()", "()(())" )为4,其他三个都为5,所以输出3. 输入描述: 输入包括字符串s(4 ≤ |s| ≤ 50,|s|表示字符串长度),保证s是一个合法的括号匹配序列。 输出描述: 输出一个正整数,满足条件的t的个数。 输入例子1: (())() 输出例子1: 3 借鉴网友答案.为了lcs最大,只需要减去一个字符,把他放到其他位置上. 字符50长度n^2可以接受. 然后判断是否是合理括号即可.合理就能cnt+1,还需要去重 a=input() def test(a): #用计数法来写更方便 cnt=0 for i in range(len(a)): if a[i]=='(': cnt+=1 else: cnt-=1 if cnt<0: return False return True memo={} #字符可以后面的往前面的放!!!!所以下面分i>j j>i2种情况分类即可. for i in range(len(a)): for j in range(len(a)): #把i位置的放到j位置上 if i==j: continue if i<j: now=a[:i]+a[i+1:j]+a[i]+a[j:] if i>j: now=a[:j]+a[i]+a[j:i]+a[i+1:] if now not in memo: memo[now]=1 if a in memo: memo.pop(a) t=list(memo.keys()) cnt=0 for i in range(len(t)): if test(t[i]): cnt+=1 print(cnt) ''' ''' [编程题] 合唱 时间限制:2秒 空间限制:131072K 小Q和牛博士合唱一首歌曲,这首歌曲由n个音调组成,每个音调由一个正整数表示。 对于每个音调要么由小Q演唱要么由牛博士演唱,对于一系列音调演唱的难度等于所有相邻音调变化幅度之和, 例如一个音调序列是8, 8, 13, 12, 那么它的难度等于|8 - 8| + |13 - 8| + |12 - 13| = 6(其中||表示绝对值)。 现在要对把这n个音调分配给小Q或牛博士,让他们演唱的难度之和最小,请你算算最小的难度和是多少。 如样例所示: 小Q选择演唱{5, 6}难度为1, 牛博士选择演唱{1, 2, 1}难度为2,难度之和为3,这一个是最小难度和的方案了。 输入描述: 输入包括两行,第一行一个正整数n(1 ≤ n ≤ 2000) 第二行n个整数v[i](1 ≤ v[i] ≤ 10^6), 表示每个音调。 输出描述: 输出一个整数,表示小Q和牛博士演唱最小的难度和是多少。 输入例子1: 5 1 5 6 2 1 输出例子1: 3 题目的意思是:把这个数组里面的随便分配到2个数组中.然后让难度和最小 动态规划: dp[i][j]表示一个人最后唱的音符是i,另一个人最后唱的音符是j,且(i>j),且歌曲只从0唱到字符i i,j的取值范围是i从0到n-1 对于每一个i:j<i 链接:https://www.nowcoder.com/questionTerminal/fddf64d5757e41ec93f3ef0c0a10b891 来源:牛客网 确定dp[i][j]的状态转移方程:(i<j) 分两种情况: a:当 j=i-1 时 例如: dp[4][3](3=4-1) 则若小Q当前弹的是第4个音调,牛博士此前刚弹完的是第3个音调,那么小Q之前弹的音调的可能情况有:2、 1、 0 (或者一个也没弹)四种可能,那么dp[4][3]= min(dp[3][2],dp[3][1],dp[3][0],一个音也没弹过)。 b:当 j!=i-1时,则dp[i][j]一定是由dp[i-1][j]转移得到的,譬如说:dp[4][2] 一定是由dp[3][2] 转移得到的,因为牛博士此前刚弹完的是第2个音调,而小Q当前要弹的是第4个音调,那么小Q之前弹的音调一定是第3个音调。 a=input() arr=[int(i)for i in input().split()] #把arr分成3个部分,或者2个部分. dp=[[0]*len(arr)for _ in range(len(arr))] for i in range(2,len(arr)):#因为下面有i-2所以从2开始 dp[i][0]=dp[i-1][0]+abs(arr[i]-arr[i-1]) #下面这行初始化最难的地方 dp[i][i-1]=dp[i-1][i-2]+abs(arr[i-1]-arr[i-2]) #把dp[i][i-1]初始化为前i-1个音调第一个人弹,最后一个音调第二个人弹(此前一个音也没弹过)。 for i in range(2,len(arr)):#2不能改成1,从2个音符开始分配即可. for j in range(i-1): dp[i][j]=dp[i-1][j]+abs(arr[i]-arr[i-1])#比较难理解 #这个特例需要讨论,这就是这个题目特俗的地方 for j in range(i-1): dp[i][i-1]=min(dp[i][i-1],dp[i-1][j]+abs(arr[i]-arr[j])) # 例如: dp[4][3](3=4-1) 则若小Q当前弹的是第4个音调,牛博士此前刚弹完的是第3个音调,那么小Q之前弹的音调的可能情况有:2、 1、 0 (或者一个也没弹)四种可能,那么dp[4][3]= min(dp[3][2],dp[3][1],dp[3][0],一个音也没弹过)。 print(min(dp[-1][:-1])) ''' ''' [编程题] 回文序列 时间限制:1秒 空间限制:32768K 如果一个数字序列逆置之后跟原序列是一样的就称这样的数字序列为回文序列。例如: {1, 2, 1}, {15, 78, 78, 15} , {112} 是回文序列, {1, 2, 2}, {15, 78, 87, 51} ,{112, 2, 11} 不是回文序列。 现在给出一个数字序列,允许使用一种转换操作: 选择任意两个相邻的数,然后从序列移除这两个数,并用这两个数字的和插入到这两个数之前的位置(只插入一个和)。 现在对于所给序列要求出最少需要多少次操作可以将其变成回文序列。 输入描述: 输入为两行,第一行为序列长度n ( 1 ≤ n ≤ 50) 第二行为序列中的n个整数item[i] (1 ≤ iteam[i] ≤ 1000),以空格分隔。 输出描述: 输出一个数,表示最少需要的转换次数 输入例子1: 4 1 1 1 3 输出例子1: 2 #暴力递归显然不行 a=int(input()) arr=[int(i)for i in input().split()] def main(arr): if arr==arr[::-1]: return 0 else: a=[] for i in range(len(arr)-1): now=arr[:i]+[(arr[i]+arr[i+1])]+arr[i+2:] a.append(1+main(now)) return min(a) print(main(arr)) #不用递归!--人生苦短我用python #首尾指针跟踪 #两个数不相等就进行加法:小的数加上相邻的值 # 看看别人的思路 #引入双端队列来模拟,常用命令append appendleft pop popleft #但是为什么这么算能解决问题呢.为什么是最少的操作数? #因为最边上2个必须优先保证相等,所以这个算法是对的 from collections import deque a=int(input()) arr=[int(i)for i in input().split()] d=deque(arr) cnt=0 while list(d)!=list(d)[::-1]: first=d[0] end=d[-1] if first>end: a=d.pop() b=d.pop() d.append(a+b) cnt+=1 continue if first==end: d.pop() d.popleft() continue if first<end: a=d.popleft() b=d.popleft() d.appendleft(a+b) cnt+=1 continue print(cnt) ''' ''' [编程题] 优雅的点 时间限制:1秒 空间限制:32768K 小易有一个圆心在坐标原点的圆,小易知道圆的半径的平方。小易认为在圆上的点而且横纵坐标都是整数的点是优雅的,小易现在想寻找一个算法计算出优雅的点的个数,请你来帮帮他。 例如:半径的平方如果为25 优雅的点就有:(+/-3, +/-4), (+/-4, +/-3), (0, +/-5) (+/-5, 0),一共12个点。 输入描述: 输入为一个整数,即为圆半径的平方,范围在32位int范围内。 输出描述: 输出为一个整数,即为优雅的点的个数 输入例子1: 25 输出例子1: 12 有关完全平方数的题目:做了这么多,总结就是一定要用到平方这个性质选一个根号n的算法 a=int(input()) r=int(a**0.5) cnt=0 for i in range(-r,r+1): tmp=a-i**2 tmp=tmp**0.5 if int(tmp)==tmp: cnt+=2 tmp=a tmp=tmp**0.5 if int(tmp)==tmp: cnt-=2 print(cnt) ''' ''' 决策树与逻辑回归的比较: 1、决策树由于采用分割的方法,所以能够深入数据细部,但同时失去了对全局的把握。一个分支一旦形成,它和别的分支或节点的关系就被切断,以后的挖掘只能在局部中行; 2、逻辑回归始终着眼于整数数据的拟合,所以对全局模式把握较好; 3、决策树比较容易上手,需要的数据预处理较少; 4、逻辑回归模型不能处理缺失值,而且对异常值敏感。因此回归之前应该处理缺失值,并尽量删除异常值 ''' ''' [编程题] 跳石板 时间限制:1秒 空间限制:32768K 小易来到了一条石板路前,每块石板上从1挨着编号为:1、2、3....... 这条石板路要根据特殊的规则才能前进:对于小易当前所在的编号为K的 石板,小易单次只能往前跳K的一个约数(不含1和K)步,即跳到K+X(X为K的一个非1和本身的约数)的位置。 小易当前处在编号为N的石板,他想跳到编号恰好为M的石板去,小易想知道最少需要跳跃几次可以到达。 例如: N = 4,M = 24: 4->6->8->12->18->24 于是小易最少需要跳跃5次,就可以从4号石板跳到24号石板 输入描述: 输入为一行,有两个整数N,M,以空格隔开。 (4 ≤ N ≤ 100000) (N ≤ M ≤ 100000) 输出描述: 输出小易最少需要跳跃的步数,如果不能到达输出-1 输入例子1: 4 24 输出例子1: 5 注意10万的数量级可以用n**(3/2)这个数量级的算法 其中求因子是n**0.5数量级 动态规划是n所以可以动态规划逐步来解决. first,end=map(int,input().split()) def yinzi(x): yinzi=[] for i in range(2,int(x**0.5)+1): if x%i==0: yinzi.append(i) yinzi.append(x//i) return yinzi dp=[float('inf')]*(end*2)#dp[i]表示走到i步需要多少个跳跃 dp[first]=0 for i in range(first,end+1): if dp[i]==float('inf'): continue tmp=yinzi(i) for j in tmp: dp[i+j]=min(dp[i+j],dp[i]+1) if (dp[end])!=float('inf'): print(dp[(end)]) else: print(-1) 还是过不了之只有百分之80,因为python3比python2速度慢!python2能过 ''' ''' 3.java与c++的区别,知道多少答多少 C++有指针,java没有 C++创建对象之后,使用完调用delete方法将其销毁,Java通过垃圾回收机制 C++中声明常量的关键字是“const”;java中声明常量的关键字是“final” Java单继承,C++多继承 C++不支持字符串,java通过类对象实现字符串 C++有goto,Java没有goto(作为保留字) --------------------- 作者:aquaphh 来源:CSDN 原文:https://blog.csdn.net/aquaphh/article/details/82153953?utm_source=copy 版权声明:本文为博主原创文章,转载请附上博文链接! ''' ''' [编程题] 暗黑的字符串 时间限制:1秒 空间限制:32768K 一个只包含'A'、'B'和'C'的字符串,如果存在某一段长度为3的连续子串中恰好'A'、'B'和'C'各有一个,那么这个字符串就是纯净的,否则这个字符串就是暗黑的。例如: BAACAACCBAAA 连续子串"CBA"中包含了'A','B','C'各一个,所以是纯净的字符串 AABBCCAABB 不存在一个长度为3的连续子串包含'A','B','C',所以是暗黑的字符串 你的任务就是计算出长度为n的字符串(只包含'A'、'B'和'C'),有多少个是暗黑的字符串。 输入描述: 输入一个整数n,表示字符串长度(1 ≤ n ≤ 30) 输出描述: 输出一个整数表示有多少个暗黑字符串 输入例子1: 2 3 输出例子1: 9 21 看暗黑的定义.就是任意一个长度为3的子串都必须有重复的字母. #做了这些动态规划的问题:感觉一定要把握问题的最后属性,这个属性总是用来切分问题 #比如这个问题就是用最后2个字母是否相同来做问题的切分和递归分类的!类似最大上升序列问题也是讨论最后的必须取到的index是几.这个最后什么的属性总是动态规划问题的关键!@ arr=[int(i)for i in input().split()] #f1表示长度n最后2个字母相同的排列数 #f2表示长度n最后2个字母不相同的排列数 def f1(n): if n==2: return 3 if n==3: return 9 else: return 3*f1(n-2)+2*f2(n-2) def f2(n): if n==2: return 6 if n==3: return 12 else: return 4*f1(n-2)+3*f2(n-2) for i in range(len(arr)): print(f1(arr[i])+f2(arr[i])) ''' ''' [编程题] 数字翻转 时间限制:1秒 空间限制:32768K 对于一个整数X,定义操作rev(X)为将X按数位翻转过来,并且去除掉前导0。例如: 如果 X = 123,则rev(X) = 321; 如果 X = 100,则rev(X) = 1. 现在给出整数x和y,要求rev(rev(x) + rev(y))为多少? 输入描述: 输入为一行,x、y(1 ≤ x、y ≤ 1000),以空格隔开。 输出描述: 输出rev(rev(x) + rev(y))的值 输入例子1: 123 100 输出例子1: 223 x,y=map(int,input().split()) x=str(x)[::-1] y=str(y)[::-1] x=int(x) y=int(y) new=x+y new=str(new)[::-1] print(int(new)) ''' ''' 看看对抗神经网络 大多数情况下,对抗网络作为非监督学习的代表,将无监督问题转化为有监督问题,两个方面解释: 通过添加噪声,在原样本基础上进行变换,得到的样本发生了微妙的变化,将“panda”错判成 “gibbon”。相信大家一定接触过 Data Augmentation,为什么同样是添加噪声,得到的结果却是迥然不同呢?实际上是我们在梯度方向上做了一点非常小的变化,导致模型就无法正确的分类。 --------------------- 作者:linolzhang 来源:CSDN 原文:https://blog.csdn.net/linolzhang/article/details/59730669?utm_source=copy 版权声明:本文为博主原创文章,转载请附上博文链接! ''' ''' 口天丶木乔 优化-最小化损失函数的三种主要方法:梯度下降(BGD)、随机梯度下降(SGD)、mini-batch SGD 理解区别: BGD是每一次用所有样本求梯度方向 SGD是每一次用随机的一个样本求梯度方向 mini SGD是每一次用一个batch来求梯度方向. ''' ''' 莫凡python进化算法 https://morvanzhou.github.io/tutorials/machine-learning/evolutionary-algorithm/2-00-genetic-algorithm/ 曾经写过遗传算法解决背包问题. # """ # Visualize Genetic Algorithm to find a maximum point in a function. # Visit my tutorial website for more: https://morvanzhou.github.io/tutorials/ # """ import numpy as np import matplotlib.pyplot as plt DNA_SIZE = 10 # DNA length POP_SIZE = 100 # population size CROSS_RATE = 0.8 # mating probability (DNA crossover) MUTATION_RATE = 0.003 # mutation probability N_GENERATIONS = 200 X_BOUND = [0, 5] # x upper and lower bounds def F(x): return np.sin(10*x)*x + np.cos(2*x)*x # to find the maximum of this function # find non-zero fitness for selection def get_fitness(pred): return pred + 1e-3 - np.min(pred) # convert binary DNA to decimal and normalize it to a range(0, 5) def translateDNA(pop): return pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2**DNA_SIZE-1) * X_BOUND[1] def select(pop, fitness): # nature selection wrt pop's fitness idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True, p=fitness/fitness.sum()) return pop[idx] def crossover(parent, pop): # mating process (genes crossover) if np.random.rand() < CROSS_RATE: i_ = np.random.randint(0, POP_SIZE, size=1) # select another individual from pop cross_points = np.random.randint(0, 2, size=DNA_SIZE).astype(np.bool) # choose crossover points parent[cross_points] = pop[i_, cross_points] # mating and produce one child return parent def mutate(child): for point in range(DNA_SIZE): if np.random.rand() < MUTATION_RATE: child[point] = 1 if child[point] == 0 else 0 return child pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE)) # initialize the pop DNA plt.ion() # something about plotting x = np.linspace(*X_BOUND, 200) plt.plot(x, F(x)) for _ in range(N_GENERATIONS): F_values = F(translateDNA(pop)) # compute function value by extracting DNA # something about plotting if 'sca' in globals(): sca.remove() sca = plt.scatter(translateDNA(pop), F_values, s=200, lw=0, c='red', alpha=0.5); plt.pause(0.05) # GA part (evolution) fitness = get_fitness(F_values) print("Most fitted DNA: ", pop[np.argmax(fitness), :]) pop = select(pop, fitness) pop_copy = pop.copy() for parent in pop: child = crossover(parent, pop_copy) child = mutate(child) parent[:] = child # parent is replaced by its child plt.ioff(); plt.show() # """ # Visualize Genetic Algorithm to match the target phrase. # Visit my tutorial website for more: https://morvanzhou.github.io/tutorials/ # """ import numpy as np TARGET_PHRASE = 'You get it!' # target DNA POP_SIZE = 300 # population size CROSS_RATE = 0.4 # mating probability (DNA crossover) MUTATION_RATE = 0.01 # mutation probability N_GENERATIONS = 1000 DNA_SIZE = len(TARGET_PHRASE) TARGET_ASCII = np.fromstring(TARGET_PHRASE, dtype=np.uint8) # convert string to number ASCII_BOUND = [32, 126] class GA(object): def __init__(self, DNA_size, DNA_bound, cross_rate, mutation_rate, pop_size): self.DNA_size = DNA_size DNA_bound[1] += 1 self.DNA_bound = DNA_bound self.cross_rate = cross_rate self.mutate_rate = mutation_rate self.pop_size = pop_size self.pop = np.random.randint(*DNA_bound, size=(pop_size, DNA_size)).astype(np.int8) # int8 for convert to ASCII #初始化所有的样本 def translateDNA(self, DNA): # convert to readable string return DNA.tostring().decode('ascii') def get_fitness(self): # count how many character matches match_count = (self.pop == TARGET_ASCII).sum(axis=1) return match_count def select(self): fitness = self.get_fitness() + 1e-4 # add a small amount to avoid all zero fitness idx = np.random.choice(np.arange(self.pop_size), size=self.pop_size, replace=True, p=fitness/fitness.sum()) return self.pop[idx] def crossover(self, parent, pop): #parent是爸爸,pop是妈妈们,在pop里面选一个进行crossover if np.random.rand() < self.cross_rate: i_ = np.random.randint(0, self.pop_size, size=1) # select another individual from pop cross_points = np.random.randint(0, 2, self.DNA_size).astype(np.bool) # choose crossover points parent[cross_points] = pop[i_, cross_points] #把母亲基因给父亲,返回父亲即可 # mating and produce one child return parent def mutate(self, child): for point in range(self.DNA_size): if np.random.rand() < self.mutate_rate: child[point] = np.random.randint(*self.DNA_bound) # choose a random ASCII index return child def evolve(self): pop = self.select() pop_copy = pop.copy() for parent in pop: # for every parent child = self.crossover(parent, pop_copy) child = self.mutate(child) parent[:] = child self.pop = pop if __name__ == '__main__': ga = GA(DNA_size=DNA_SIZE, DNA_bound=ASCII_BOUND, cross_rate=CROSS_RATE, mutation_rate=MUTATION_RATE, pop_size=POP_SIZE) for generation in range(N_GENERATIONS): fitness = ga.get_fitness() best_DNA = ga.pop[np.argmax(fitness)] best_phrase = ga.translateDNA(best_DNA) print('Gen', generation, ': ', best_phrase) if best_phrase == TARGET_PHRASE: break ga.evolve() # """ # Visualize Genetic Algorithm to find the shortest path for travel sales problem. # Visit my tutorial website for more: https://morvanzhou.github.io/tutorials/ # """ import matplotlib.pyplot as plt import numpy as np N_CITIES = 20 # DNA size CROSS_RATE = 0.1 MUTATE_RATE = 0.02 POP_SIZE = 500 N_GENERATIONS = 500 class GA(object): def __init__(self, DNA_size, cross_rate, mutation_rate, pop_size, ): self.DNA_size = DNA_size self.cross_rate = cross_rate self.mutate_rate = mutation_rate self.pop_size = pop_size self.pop = np.vstack([np.random.permutation(DNA_size) for _ in range(pop_size)]) def translateDNA(self, DNA, city_position): # get cities' coord in order line_x = np.empty_like(DNA, dtype=np.float64) line_y = np.empty_like(DNA, dtype=np.float64) for i, d in enumerate(DNA): city_coord = city_position[d] line_x[i, :] = city_coord[:, 0] line_y[i, :] = city_coord[:, 1] return line_x, line_y def get_fitness(self, line_x, line_y): total_distance = np.empty((line_x.shape[0],), dtype=np.float64) for i, (xs, ys) in enumerate(zip(line_x, line_y)): total_distance[i] = np.sum(np.sqrt(np.square(np.diff(xs)) + np.square(np.diff(ys)))) fitness = np.exp(self.DNA_size * 2 / total_distance) return fitness, total_distance def select(self, fitness): idx = np.random.choice(np.arange(self.pop_size), size=self.pop_size, replace=True, p=fitness / fitness.sum()) return self.pop[idx] def crossover(self, parent, pop): if np.random.rand() < self.cross_rate: i_ = np.random.randint(0, self.pop_size, size=1) # select another individual from pop cross_points = np.random.randint(0, 2, self.DNA_size).astype(np.bool) # choose crossover points keep_city = parent[~cross_points] # find the city number swap_city = pop[i_, np.isin(pop[i_].ravel(), keep_city, invert=True)] parent[:] = np.concatenate((keep_city, swap_city)) return parent def mutate(self, child): for point in range(self.DNA_size): if np.random.rand() < self.mutate_rate: swap_point = np.random.randint(0, self.DNA_size) swapA, swapB = child[point], child[swap_point] child[point], child[swap_point] = swapB, swapA return child def evolve(self, fitness): pop = self.select(fitness) pop_copy = pop.copy() for parent in pop: # for every parent child = self.crossover(parent, pop_copy) child = self.mutate(child) parent[:] = child self.pop = pop class TravelSalesPerson(object): def __init__(self, n_cities): self.city_position = np.random.rand(n_cities, 2) plt.ion() def plotting(self, lx, ly, total_d): plt.cla() plt.scatter(self.city_position[:, 0].T, self.city_position[:, 1].T, s=100, c='k') plt.plot(lx.T, ly.T, 'r-') plt.text(-0.05, -0.05, "Total distance=%.2f" % total_d, fontdict={'size': 20, 'color': 'red'}) plt.xlim((-0.1, 1.1)) plt.ylim((-0.1, 1.1)) plt.pause(0.01) ga = GA(DNA_size=N_CITIES, cross_rate=CROSS_RATE, mutation_rate=MUTATE_RATE, pop_size=POP_SIZE) env = TravelSalesPerson(N_CITIES) for generation in range(N_GENERATIONS): lx, ly = ga.translateDNA(ga.pop, env.city_position) fitness, total_distance = ga.get_fitness(lx, ly) ga.evolve(fitness) best_idx = np.argmax(fitness) print('Gen:', generation, '| best fit: %.2f' % fitness[best_idx],) env.plotting(lx[best_idx], ly[best_idx], total_distance[best_idx]) plt.ioff() plt.show() ''' ''' #类似的一个微生物算法 #随机在population里面抽选2个,然后胜利的不变,loser抽取胜利的部分基因做变异,之后 #都放回pop即可.这个算法比上面的遗传算法快.下面是例子 """ Visualize Microbial Genetic Algorithm to find the maximum point in a graph. Visit my tutorial website for more: https://morvanzhou.github.io/tutorials/ """ import numpy as np import matplotlib.pyplot as plt DNA_SIZE = 10 # DNA length POP_SIZE = 20 # population size CROSS_RATE = 0.6 # mating probability (DNA crossover) MUTATION_RATE = 0.01 # mutation probability N_GENERATIONS = 200 X_BOUND = [0, 5] # x upper and lower bounds def F(x): return np.sin(10*x)*x + np.cos(2*x)*x # to find the maximum of this function class MGA(object): def __init__(self, DNA_size, DNA_bound, cross_rate, mutation_rate, pop_size): self.DNA_size = DNA_size DNA_bound[1] += 1 self.DNA_bound = DNA_bound self.cross_rate = cross_rate self.mutate_rate = mutation_rate self.pop_size = pop_size # initial DNAs for winner and loser self.pop = np.random.randint(*DNA_bound, size=(1, self.DNA_size)).repeat(pop_size, axis=0) def translateDNA(self, pop): # convert binary DNA to decimal and normalize it to a range(0, 5) return pop.dot(2 ** np.arange(self.DNA_size)[::-1]) / float(2 ** self.DNA_size - 1) * X_BOUND[1] def get_fitness(self, product): return product # it is OK to use product value as fitness in here def crossover(self, loser_winner): # crossover for loser cross_idx = np.empty((self.DNA_size,)).astype(np.bool) for i in range(self.DNA_size): cross_idx[i] = True if np.random.rand() < self.cross_rate else False # crossover index loser_winner[0, cross_idx] = loser_winner[1, cross_idx] # assign winners genes to loser return loser_winner def mutate(self, loser_winner): # mutation for loser mutation_idx = np.empty((self.DNA_size,)).astype(np.bool) for i in range(self.DNA_size): mutation_idx[i] = True if np.random.rand() < self.mutate_rate else False # mutation index # flip values in mutation points loser_winner[0, mutation_idx] = ~loser_winner[0, mutation_idx].astype(np.bool) return loser_winner def evolve(self, n): # nature selection wrt pop's fitness for _ in range(n): # random pick and compare n times sub_pop_idx = np.random.choice(np.arange(0, self.pop_size), size=2, replace=False) sub_pop = self.pop[sub_pop_idx] # pick 2 from pop product = F(self.translateDNA(sub_pop)) fitness = self.get_fitness(product) loser_winner_idx = np.argsort(fitness) loser_winner = sub_pop[loser_winner_idx] # the first is loser and second is winner loser_winner = self.crossover(loser_winner) loser_winner = self.mutate(loser_winner) self.pop[sub_pop_idx] = loser_winner DNA_prod = self.translateDNA(self.pop) pred = F(DNA_prod) return DNA_prod, pred plt.ion() # something about plotting x = np.linspace(*X_BOUND, 200) plt.plot(x, F(x)) ga = MGA(DNA_size=DNA_SIZE, DNA_bound=[0, 1], cross_rate=CROSS_RATE, mutation_rate=MUTATION_RATE, pop_size=POP_SIZE) for _ in range(N_GENERATIONS): # 100 generations DNA_prod, pred = ga.evolve(5) # natural selection, crossover and mutation # something about plotting if 'sca' in globals(): sca.remove() sca = plt.scatter(DNA_prod, pred, s=200, lw=0, c='red', alpha=0.5); plt.pause(0.05) plt.ioff();plt.show() ''' ''' #进化学习:跟遗传学习不同的是他是用实数来进行crossover,用高斯分布来进行mutate """ The Evolution Strategy can be summarized as the following term: {mu/rho +, lambda}-ES Here we use following term to find a maximum point. {n_pop/n_pop + n_kid}-ES Visit my tutorial website for more: https://morvanzhou.github.io/tutorials/ """ import numpy as np import matplotlib.pyplot as plt DNA_SIZE = 1 # DNA (real number) DNA_BOUND = [0, 5] # solution upper and lower bounds N_GENERATIONS = 200 POP_SIZE = 100 # population size N_KID = 50 # n kids per generation def F(x): return np.sin(10*x)*x + np.cos(2*x)*x # to find the maximum of this function # find non-zero fitness for selection def get_fitness(pred): return pred.flatten() def make_kid(pop, n_kid): # generate empty kid holder kids = {'DNA': np.empty((n_kid, DNA_SIZE))} kids['mut_strength'] = np.empty_like(kids['DNA']) for kv, ks in zip(kids['DNA'], kids['mut_strength']): # crossover (roughly half p1 and half p2) p1, p2 = np.random.choice(np.arange(POP_SIZE), size=2, replace=False) cp = np.random.randint(0, 2, DNA_SIZE, dtype=np.bool) # crossover points kv[cp] = pop['DNA'][p1, cp] kv[~cp] = pop['DNA'][p2, ~cp] ks[cp] = pop['mut_strength'][p1, cp] ks[~cp] = pop['mut_strength'][p2, ~cp] # mutate (change DNA based on normal distribution) ks[:] = np.maximum(ks + (np.random.rand(*ks.shape)-0.5), 0.) # must > 0 kv += ks * np.random.randn(*kv.shape) kv[:] = np.clip(kv, *DNA_BOUND) # clip the mutated value return kids def kill_bad(pop, kids): # put pop and kids together for key in ['DNA', 'mut_strength']: pop[key] = np.vstack((pop[key], kids[key])) fitness = get_fitness(F(pop['DNA'])) # calculate global fitness idx = np.arange(pop['DNA'].shape[0]) good_idx = idx[fitness.argsort()][-POP_SIZE:] # selected by fitness ranking (not value) for key in ['DNA', 'mut_strength']: pop[key] = pop[key][good_idx] return pop pop = dict(DNA=5 * np.random.rand(1, DNA_SIZE).repeat(POP_SIZE, axis=0), # initialize the pop DNA values mut_strength=np.random.rand(POP_SIZE, DNA_SIZE)) # initialize the pop mutation strength values plt.ion() # something about plotting x = np.linspace(*DNA_BOUND, 200) plt.plot(x, F(x)) for _ in range(N_GENERATIONS): # something about plotting if 'sca' in globals(): sca.remove() sca = plt.scatter(pop['DNA'], F(pop['DNA']), s=200, lw=0, c='red', alpha=0.5); plt.pause(0.05) # ES part kids = make_kid(pop, N_KID) pop = kill_bad(pop, kids) # keep some good parent for elitism plt.ioff(); plt.show() ''' ''' [编程题] 最大的奇约数 时间限制:1秒 空间限制:32768K 小易是一个数论爱好者,并且对于一个数的奇数约数十分感兴趣。一天小易遇到这样一个问题: 定义函数f(x)为x最大的奇数约数,x为正整数。 例如:f(44) = 11. 现在给出一个N,需要求出 f(1) + f(2) + f(3).......f(N) 例如: N = 7 f(1) + f(2) + f(3) + f(4) + f(5) + f(6) + f(7) = 1 + 1 + 3 + 1 + 5 + 3 + 7 = 21 小易计算这个问题遇到了困难,需要你来设计一个算法帮助他。 输入描述: 输入一个整数N (1 ≤ N ≤ 1000000000) 1e9 输出描述: 输出一个整数,即为f(1) + f(2) + f(3).......f(N) 输入例子1: 7 输出例子1: 21 看数量级1e9就知道是找规律,递归不好使. 显然奇数就是他自己,处理偶数即可. 用二进制说法就是把一个数的右边0都去掉就是最大奇数因子 还是不好分析: 答案是2分递归法: # /* # * 奇数的最大约数就是本身。问题就是求所有f(i), i为偶数的和 因为要求的是最大奇约数,所以f(2k) = f(k),所以f(2) + f(4) # * + ... + f(2k) = f(1) + f(2) + ... + f(k); # * # * sum(n) = sum (n / 2) + 1 + 3 + ... + n - 1 = sum (n/2) + n*n/4(n 为偶数) # * # * = sum (n - 1) + n (n为奇数) # * # * # */ #2分递归第一次见到.. a=int(input()) def main(a): if a==1: return 1 if a%2==0: return main(a//2)+(a)**2//4 else: return main(a-1)+a print(int(main(a))) ''' ''' [编程题] 买苹果 时间限制:1秒 空间限制:32768K 小易去附近的商店买苹果,奸诈的商贩使用了捆绑交易,只提供6个每袋和8个每袋的包装(包装不可拆分)。 可是小易现在只想购买恰好n个苹果,小易想购买尽量少的袋数方便携带。如果不能购买恰好n个苹果,小易将不会购买。 输入描述: 输入一个整数n,表示小易想购买n(1 ≤ n ≤ 100)个苹果 输出描述: 输出一个整数表示最少需要购买的袋数,如果不能买恰好n个苹果则输出-1 输入例子1: 20 输出例子1: 3 a=int(input()) def main(a):#返回拼重量a最少需要多少个袋子 if a<8 and a!=6: return -float('inf') if a==8 or a==6: return 1 case1=main(a-8)+1 case2=main(a-6)+1 if case1!=-float('inf') and case2!=-float('inf'): return min(case1,case2) if case1==-float('inf') and case2!=-float('inf'): return case2 if case1!=-float('inf') and case2==-float('inf'): return case1 if case1==-float('inf') and case2==-float('inf'): return -float('inf') if main(a)==-float('inf'): print(-1) else: print(main(a)) ''' ''' [编程题] 计算糖果 时间限制:1秒 空间限制:32768K A,B,C三个人是好朋友,每个人手里都有一些糖果,我们不知道他们每个人手上具体有多少个糖果,但是我们知道以下的信息: A - B, B - C, A + B, B + C. 这四个数值.每个字母代表每个人所拥有的糖果数. 现在需要通过这四个数值计算出每个人手里有多少个糖果,即A,B,C。这里保证最多只有一组整数A,B,C满足所有题设条件。 输入描述: 输入为一行,一共4个整数,分别为A - B,B - C,A + B,B + C,用空格隔开。 范围均在-30到30之间(闭区间)。 输出描述: 输出为一行,如果存在满足的整数A,B,C则按顺序输出A,B,C,用空格隔开,行末无空格。 如果不存在这样的整数A,B,C,则输出No 输入例子1: 1 -2 3 4 输出例子1: 2 1 3 arr=[int(i)for i in input().split()] a=(arr[0]+arr[2])/2 b=(arr[2]-arr[0])/2 c=(arr[3]-arr[1])/2 if int(a)!=a or int(b)!=b or int(c)!=c or int(b)-int(c)!=arr[1]: print('No') else: print(int(a),int(b),int(c)) ''' ''' 交叉熵: 给定数据集(xi,yi) l(w,b)=sum ln p(yi|xi;w,b)越大越好 或者是L=-sum ylogy^+(1-y)log(1-y^) ''' ''' [编程题] 双核处理 时间限制:1秒 空间限制:32768K 一种双核CPU的两个核能够同时的处理任务,现在有n个已知数据量的任务需要交给CPU处理,假设已知CPU的每个核1秒可以处理1kb,每个核同时只能处理一项任务。n个任务可以按照任意顺序放入CPU进行处理,现在需要设计一个方案让CPU处理完这批任务所需的时间最少,求这个最小的时间。 输入描述: 输入包括两行: 第一行为整数n(1 ≤ n ≤ 50) 第二行为n个整数length[i](1024 ≤ length[i] ≤ 4194304),表示每个任务的长度为length[i]kb,每个数均为1024的倍数。 输出描述: 输出一个整数,表示最少需要处理的时间 输入例子1: 5 3072 3072 7168 3072 1024 输出例子1: 9216 a=input() arr=[int(i)for i in input().split()] for i in range(len(arr)): arr[i]//=1024 #把问题切换为weight=value,总大小sum/2的01背包问题. if arr!=[]: all=sum(arr)//2 dp=[[0]*(all+1) for _ in range(len(arr))] for i in range(len(arr)): for j in range((all+1)): if arr[i]>j: dp[i][j]=dp[i-1][j] else: dp[i][j]=max(dp[i-1][j],dp[i-1][j-arr[i]]+arr[i]) k=(max(dp[-1]) ) print(max(k,sum(arr)-k)*1024) if arr==[]: print(0) ''' ''' #0,1背包 arr=[4,5,7,8,2] val=[4,1,2,1,1] pack=10 #dp[i][j]背包总大小j,考虑完第i个物品之后,背包里面的总价值最大值. dp=[[0]*(pack+1) for _ in range(len(arr))] for i in range(len(arr)): for j in range((pack)): if arr[i]>j: dp[i][j]=dp[i-1][j] else: dp[i][j]=max(dp[i-1][j],dp[i-1][j-arr[i]]+val[i]) print(max(dp[-1])) ''' ''' [编程题] 赶去公司 时间限制:1秒 空间限制:32768K 终于到周末啦!小易走在市区的街道上准备找朋友聚会,突然服务器发来警报,小易需要立即回公司修复这个紧急bug。假设市区是一个无限大的区域,每条街道假设坐标是(X,Y),小易当前在(0,0)街道,办公室在(gx,gy)街道上。小易周围有多个出租车打车点,小易赶去办公室有两种选择,一种就是走路去公司,另外一种就是走到一个出租车打车点,然后从打车点的位置坐出租车去公司。每次移动到相邻的街道(横向或者纵向)走路将会花费walkTime时间,打车将花费taxiTime时间。小易需要尽快赶到公司去,现在小易想知道他最快需要花费多少时间去公司。 输入描述: 输入数据包括五行: 第一行为周围出租车打车点的个数n(1 ≤ n ≤ 50) 第二行为每个出租车打车点的横坐标tX[i] (-10000 ≤ tX[i] ≤ 10000) 第三行为每个出租车打车点的纵坐标tY[i] (-10000 ≤ tY[i] ≤ 10000) 第四行为办公室坐标gx,gy(-10000 ≤ gx,gy ≤ 10000),以空格分隔 第五行为走路时间walkTime(1 ≤ walkTime ≤ 1000)和taxiTime(1 ≤ taxiTime ≤ 1000),以空格分隔 输出描述: 输出一个整数表示,小易最快能赶到办公室的时间 输入例子1: 1 3 0 5 0 10 20 输出例子1: 50 Python3(3.5.2)重置自测 1 提交运行 提前交卷下一题 收藏本题 标记一 #这个题目直接分情况挨个计算即可 ''' ''' [编程题] 调整队形 时间限制:1秒 空间限制:32768K # 在幼儿园有n个小朋友排列为一个队伍,从左到右一个挨着一个编号为(0~n-1)。其中有一些是男生,有一些是女生,男生用'B'表示,女生用'G'表示。小朋友们都很顽皮,当一个男生挨着的是女生的时候就会发生矛盾。作为幼儿园的老师,你需要让男生挨着女生或者女生挨着男生的情况最少。你只能在原队形上进行调整,每次调整只能让相邻的两个小朋友交换位置,现在需要尽快完成队伍调整,你需要计算出最少需要调整多少次可以让上述情况最少。例如: GGBBG -> GGBGB -> GGGBB 这样就使之前的两处男女相邻变为一处相邻,需要调整队形2次 输入描述: 输入数据包括一个长度为n且只包含G和B的字符串.n不超过50. 输出描述: 输出一个整数,表示最少需要的调整队伍的次数 输入例子1: GGBBG 输出例子1: 2 Python3(3.5.2)重置自测 1 a=input() arr=[] for i in range(len(a)): arr.append(a[i]) #一种方案是G到左边即可,B自动会都跑右边 cnt=0 tmp=arr[:] start=0#start用来记录当前i左边最后一个G的位置+1 for i in range(len(tmp)): if start!=i and tmp[i]=="G": cnt+=i-start if tmp[i]=='G': start+=1 #下面方案是把B都放左边. cnt2=0 start=0 for i in range(len(tmp)): if start!=i and tmp[i]=="B": cnt2+=i-start if tmp[i]=='B': start+=1 print(min(cnt,cnt2)) 提交运行 ''' ''' [编程题] 消除重复元素 时间限制:1秒 空间限制:32768K 小易有一个长度为n序列,小易想移除掉里面的重复元素,但是小易想是对于每种元素保留最后出现的那个。小易遇到了困难,希望你来帮助他。 输入描述: 输入包括两行: 第一行为序列长度n(1 ≤ n ≤ 50) 第二行为n个数sequence[i](1 ≤ sequence[i] ≤ 1000),以空格分隔 输出描述: 输出消除重复元素之后的序列,以空格分隔,行末无空格 输入例子1: 9 100 100 100 99 99 99 100 100 100 输出例子1: 99 100 Python3(3.5.2)重置自测 1 提交运行 提前交卷下一题 收藏本题 标记一下 提交结果有问题? 收起答题卡 1 2 3 a=input() arr=[int(i)for i in input().split()] memo=[0]*len(arr) #双重for循环不就完事 for i in range(len(arr)): for j in range(i+1,len(arr)): if arr[i]==arr[j]: break else: memo[i]=1 out=[] for i in range(len(memo)): if memo[i]!=0: out.append(str(arr[i])) print(' '.join(out)) ''' ''' [编程题] 魔力手环 时间限制:1秒 空间限制:32768K 小易拥有一个拥有魔力的手环上面有n个数字(构成一个环),当这个魔力手环每次使用魔力的时候就会发生一种奇特的变化:每个数字会变成自己跟后面一个数字的和(最后一个数字的后面一个数字是第一个),一旦某个位置的数字大于等于100就马上对100取模(比如某个位置变为103,就会自动变为3).现在给出这个魔力手环的构成,请你计算出使用k次魔力之后魔力手环的状态。 输入描述: 输入数据包括两行: 第一行为两个整数n(2 ≤ n ≤ 50)和k(1 ≤ k ≤ 2000000000),以空格分隔 第二行为魔力手环初始的n个数,以空格分隔。范围都在0至99. 输出描述: 输出魔力手环使用k次之后的状态,以空格分隔,行末无空格。 输入例子1: 3 2 1 2 3 输出例子1: 8 9 7 Python3(3.5.2)重置自测 1 先找规律: 比如3个数: a,b,c turn1: a+b b+c c+a turn2: a+2b+c b+2c+a c+2a+b turn3: 2a+3b+3c 2b+3c+3a 2c+3a+3b turn4: 5a+5b+6c 5b+6a+5c 5c+5a+6b 提交运行 提前交卷下一题 收藏本题 标记一下 提交结果有问题? 收起答题卡 ''' n,k=map(int,input().split())#题目k取2e11 arr=[int(i)for i in input().split()] #看了网友的答案,原来这种高效率递归问题用矩阵幂来解决. #(a1,....an)=(a1,....an)(x1,...xn) 就是对角线和次对焦都是1的矩阵. #矩阵高次幂用算2次.....2^n次拼起来即可. def multi(a,b):#a,b是同介方阵 c=[[0]*len(a)]*len(a)
继续做算法题:继续保存一波:

#下面这一段用一个txt来保存input的信息来模拟input.最后提交代码时候删除这一段即可. a9999=open('1.txt','r') def input(): return a9999.readline().rstrip(' ') #输入数据的一些模板 # n,a=map(int,input().split()) # arr=[int(i)for i in input().split()] # 格式化输出 # print('%.2f'%(maxi/2)) ''' # 最大公约数用 import fractions fractions.gcd(a,b) #多个分隔符: import re b=re.split('[+*-]',a) ''' ''' [编程题] 魔力手环 时间限制:1秒 空间限制:32768K 小易拥有一个拥有魔力的手环上面有n个数字(构成一个环),当这个魔力手环每次使用魔力的时候就会发生一种奇特的变化:每个数字会变成自己跟后面一个数字的和(最后一个数字的后面一个数字是第一个),一旦某个位置的数字大于等于100就马上对100取模(比如某个位置变为103,就会自动变为3).现在给出这个魔力手环的构成,请你计算出使用k次魔力之后魔力手环的状态。 输入描述: 输入数据包括两行: 第一行为两个整数n(2 ≤ n ≤ 50)和k(1 ≤ k ≤ 2000000000),以空格分隔 第二行为魔力手环初始的n个数,以空格分隔。范围都在0至99. 输出描述: 输出魔力手环使用k次之后的状态,以空格分隔,行末无空格。 输入例子1: 3 2 1 2 3 输出例子1: 8 9 7 Python3(3.5.2)重置自测 1 先找规律: 比如3个数: a,b,c turn1: a+b b+c c+a turn2: a+2b+c b+2c+a c+2a+b turn3: 2a+3b+3c 2b+3c+3a 2c+3a+3b turn4: 5a+5b+6c 5b+6a+5c 5c+5a+6b #只能这样了,应该是因为python3的速度太慢了 #看了网友的答案,原来这种高效率递归问题用矩阵幂来解决. #(a1,....an)=(a1,....an)(x1,...xn) 就是对角线和次对焦都是1的矩阵. #矩阵高次幂用算2次.....2^n次拼起来即可. n,k=map(int,input().split())#题目k取2e11 arr=[int(i)for i in input().split()] def multi(a,b):#a,b是同介方阵 c=[[0]*len(a)for _ in range(len(a))] #注意二维矩阵的写法,外层不要写乘因为list的mute属性问题!!!!!!! for i in range(len(a)): for j in range(len(a)): for k in range(len(a)): c[i][j]+=a[i][k]*b[k][j] c[i][j]%=100 return (c) matrix=[[0]*len(arr)for _ in range (len(arr))] #变换矩阵 matrix[0][0]=1 matrix[0][len(matrix)-1]=1 for i in range(1,len(matrix)): matrix[i][i]=1 matrix[i][i-1]=1 def multiK(mat,k):#求矩阵mat的k次幂,这个算法需要熟悉理解 danwei=[[0]*len(mat)for _ in range(len(mat))] for i in range(len(danwei)): danwei[i][i]=1 out=danwei #这里用单位矩阵来出事话 while k : if k&1==1:#当k的2进制最后一位是1,那么输出就乘一下mat,然后mat自平方,k>>1 out = multi(out,mat) mat = multi(mat,mat) k = k>>1 else: mat = multi(mat,mat) k = k>>1 return out #下面把arr跟multiK(matrix,k)乘一下,注意行列 out=[0]*len(matrix) for i in range(len(matrix)): for j in range(len(matrix)): out[i]+=arr[j]*multiK(matrix,k)[j][i] out[i]%=100 for i in range(len(out)): out[i]=str(out[i]) print(' '.join(out)) 提交运行 提前交卷下一题 收藏本题 标记一下 提交结果有问题? 收起答题卡 ''' ''' # [编程题] 工作安排 # 时间限制:1秒 # 空间限制:32768K # 现在有n位工程师和6项工作(编号为0至5),现在给出每个人能够胜任的工作序号表(用一个字符串表示,比如:045,表示某位工程师能够胜任0号,4号,5号工作)。现在需要进行工作安排,每位工程师只能被安排到自己能够胜任的工作当中去,两位工程师不能安排到同一项工作当中去。如果两种工作安排中有一个人被安排在的工作序号不一样就被视为不同的工作安排,现在需要计算出有多少种不同工作安排计划。 输入描述: 输入数据有n+1行: 第一行为工程师人数n(1 ≤ n ≤ 6) 接下来的n行,每行一个字符串表示第i(1 ≤ i ≤ n)个人能够胜任的工作(字符串不一定等长的) 输出描述: 输出一个整数,表示有多少种不同的工作安排方案 输入例子1: 6 012345 012345 012345 012345 012345 012345 输出例子1: 720 n=int(input()) arr=[input() for _ in range(n)] left=range(6) def main(dex,left):#返回剩余工作left,给dex拍工作 这个数量. cnt=0 if dex==n-1: tmp=[str(i) for i in left] a=0 for i in tmp: if i in arr[dex]: a+=1 return a for i in range(len(left)): if str(left[i]) in arr[dex]: now=left[:] now=list(now) now.pop(i) cnt+=main(dex+1,now) return cnt if left==[]: print(0) else: print(main(0,left)) ''' ''' [编程题] 集合 时间限制:1秒 空间限制:32768K 小易最近在数学课上学习到了集合的概念,集合有三个特征:1.确定性 2.互异性 3.无序性. 小易的老师给了小易这样一个集合: S = { p/q | w ≤ p ≤ x, y ≤ q ≤ z } 需要根据给定的w,x,y,z,求出集合中一共有多少个元素。小易才学习了集合还解决不了这个复杂的问题,需要你来帮助他。 输入描述: 输入包括一行: 一共4个整数分别是w(1 ≤ w ≤ x),x(1 ≤ x ≤ 100),y(1 ≤ y ≤ z),z(1 ≤ z ≤ 100).以空格分隔 输出描述: 输出集合中元素的个数 输入例子1: 1 10 1 1 输出例子1: 10 w,x,y,z=map(int,input().split()) a=set([]) for i in range(w,x+1): for j in range(y,z+1): a.add(i/j) print(len(a)) ''' ''' [编程题] 奇怪的表达式求值 时间限制:1秒 空间限制:32768K 常规的表达式求值,我们都会根据计算的优先级来计算。比如*/的优先级就高于+-。但是小易所生活的世界的表达式规则很简单,从左往右依次计算即可,而且小易所在的世界没有除法,意味着表达式中没有/,只有(+, - 和 *)。现在给出一个表达式,需要你帮忙计算出小易所在的世界这个表达式的值为多少 输入描述: 输入为一行字符串,即一个表达式。其中运算符只有-,+,*。参与计算的数字只有0~9. 保证表达式都是合法的,排列规则如样例所示。 输出描述: 输出一个数,即表达式的值 输入例子1: 3+5*7 输出例子1: 56 a=input() import re b=re.split('[+*-]',a) fuhao=[] for i in range(len(a)): if a[i] in '+-*': fuhao.append(a[i]) while len(b)!=1: tmp=b[0]+fuhao[0]+b[1] fuhao.pop(0) b=[str(eval(tmp))]+b[2:] print(b[0]) ''' ''' 编程题] 涂棋盘 时间限制:1秒 空间限制:32768K 小易有一块n*n的棋盘,棋盘的每一个格子都为黑色或者白色,小易现在要用他喜欢的红色去涂画棋盘。小易会找出棋盘中某一列中拥有相同颜色的最大的区域去涂画,帮助小易算算他会涂画多少个棋格。 输入描述: 输入数据包括n+1行: 第一行为一个整数n(1 ≤ n ≤ 50),即棋盘的大小 接下来的n行每行一个字符串表示第i行棋盘的颜色,'W'表示白色,'B'表示黑色 输出描述: 输出小易会涂画的区域大小 输入例子1: 3 BWW BBB BWB 输出例子1: 3 a=int(input()) b=[] for i in range((a)): tmp=input() base=[] for i in tmp: base.append(i) b.append(base) #不用numpy实现矩阵转至 tmp=[] for i in range(len(b)): save=[] for j in range(len(b)): save.append(b[j][i]) tmp.append(save) memo=[] for i in tmp: maxi=0 cnt=1 for j in range(1,len(i)): if i[j]==i[j-1]: cnt+=1 maxi=max(maxi,cnt) else: maxi=max(maxi,cnt) cnt=1 memo.append(maxi) print(max(memo)) ''' ''' [编程题] 小易记单词 时间限制:1秒 空间限制:32768K 小易参与了一个记单词的小游戏。游戏开始系统提供了m个不同的单词,小易记忆一段时间之后需要在纸上写出他记住的单词。小易一共写出了n个他能记住的单词,如果小易写出的单词是在系统提供的,将获得这个单词长度的平方的分数。注意小易写出的单词可能重复,但是对于每个正确的单词只能计分一次。 输入描述: 输入数据包括三行: 第一行为两个整数n(1 ≤ n ≤ 50)和m(1 ≤ m ≤ 50)。以空格分隔 第二行为n个字符串,表示小易能记住的单词,以空格分隔,每个单词的长度小于等于50。 第三行为m个字符串,系统提供的单词,以空格分隔,每个单词的长度小于等于50。 输出描述: 输出一个整数表示小易能获得的分数 输入例子1: 3 4 apple orange strawberry strawberry orange grapefruit watermelon 输出例子1: 136 n,m=map(int,input().split()) jiyi=input().split()[:n] #这个题目有bug这里面他给的多了,所以需要些:n来切片即可. xitong=input().split()[:m] jiyi=set(jiyi) xitong=set(xitong) cnt=0 for i in jiyi: if i in xitong: cnt+=len(i)**2 print(cnt) ''' ''' [编程题] 堆砖块 时间限制:1秒 空间限制:32768K 小易有n块砖块,每一块砖块有一个高度。小易希望利用这些砖块堆砌两座相同高度的塔。为了让问题简单,砖块堆砌就是简单的高度相加,某一块砖只能使用在一座塔中一次。小易现在让能够堆砌出来的两座塔的高度尽量高,小易能否完成呢。 输入描述: 输入包括两行: 第一行为整数n(1 ≤ n ≤ 50),即一共有n块砖块 第二行为n个整数,表示每一块砖块的高度height[i] (1 ≤ height[i] ≤ 500000) 输出描述: 如果小易能堆砌出两座高度相同的塔,输出最高能拼凑的高度,如果不能则输出-1. 保证答案不大于500000。 输入例子1: 3 2 3 5 输出例子1: 5 这个题目动态规划还可以.是相当可以了,非常难.因为他的递归不是按照index,而是按照高度差 ''' ''' 别人的java答案:非常牛逼: 链接:https://www.nowcoder.com/questionTerminal/040924ba0e64423b8a3fe2f75a56934a 来源:牛客网 /** 思路来自于csdn上,大概看了一次,这次是完全凭记忆写出来的,主要的就是利用动态规划的思想, dp[i][j]表示在使用前i块砖,高度差为j时低塔的高度,考虑四种情况: 1. 新砖块放在低塔上,:低塔依然是低塔,即 dp[i][j] = dp[i-1][j+high] + high; 2. 新砖块放在低塔上,低塔变成了高塔,即: dp[i][j] = dp[i-1][high-j] + high-j; 3. 新砖块放在高塔上,高塔只可能是高塔,即: dp[i][j] = dp[i-1][j-high]; 4. 放弃新砖块,不放在任何一个塔上,即: dp[i][j] = dp[i-1][j]; 最终dp[i][j]取以上四种情况的最大值即可; 如果直接定义n*sum维的数组,内存会不够,所以优化了一下内存,应该有更好的方法,再学习了 */ import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); while (sc.hasNext()) { int n = sc.nextInt(); int[] h = new int[n]; int sum = 0; for (int i = 0; i < n; i++) { h[i] = sc.nextInt(); sum += h[i]; } //sum表示所有砖块的总和 int[][] dp = new int[2][sum+1]; //dp[i][j] 定义2 是因为利用滚动数组,表示前i个砖块中,堆成的塔,高度差为j时,低塔的最高高度 所以最后需要返回i是n,j为0的时候的解即可. for (int i = 0; i < 2; i++) { for (int j = 0; j < sum + 1; j++) { dp[i][j] = Integer.MIN_VALUE; //初始化为负无穷,表示没有这种高度的堆法 } } dp[0][0] = 0; //如果没有放砖的时候,低塔为0,高度差为0 for (int i = 0; i < n; i++) { int high = h[i]; //比如放第二个砖块之前,high就是第一个砖块????????这个地方不理解 //核心就是下面4行代码! for (int j = 0; j <= sum; j++) { //非常精彩的4个推理!!!!!!!!!!!!!!!!!!!!!!!!!!!!! if(j > high) { //如果将砖块放在高塔上,则低塔高度不变,高度差增加 //之前的差是j-high,现在的高是j,high表示当前需要插入的砖的高度 dp[1][j] = Math.max(dp[1][j], dp[0][j - high]); } else {//如果当前插入砖的高度>=j //如果将砖块放在低塔上,低塔变高塔,高塔高度变低塔高度,高度差改变 dp[1][j] = Math.max(dp[1][j], dp[0][high - j] + (high - j)); } //如果将新砖块放在低塔上,并且依然是低塔,则低塔高度增加 if(j + high <= sum) dp[1][j] = Math.max(dp[1][j], dp[0][j + high] + high); //放弃该砖块,不放在任何一个塔上 dp[1][j] = Math.max(dp[1][j], dp[0][j]); } System.arraycopy(dp[1], 0, dp[0], 0, sum + 1);//交换数组的数据,所以不管数据n是多少,最后的数据总是在dp[0]里面. for (int j = 0; j <= sum; j++) { dp[1][0] = Integer.MIN_VALUE; } } if(dp[0][0] > 0) System.out.println(dp[0][0]); else System.out.println(-1); } } } ''' ''' [编程题] 分饼干 时间限制:1秒 空间限制:32768K 易老师购买了一盒饼干,盒子中一共有k块饼干,但是数字k有些数位变得模糊了,看不清楚数字具体是多少了。易老师需要你帮忙把这k块饼干平分给n个小朋友,易老师保证这盒饼干能平分给n个小朋友。现在你需要计算出k有多少种可能的数值 输入描述: 输入包括两行: 第一行为盒子上的数值k,模糊的数位用X表示,长度小于18(可能有多个模糊的数位) 第二行为小朋友的人数n 输出描述: 输出k可能的数值种数,保证至少为1 输入例子1: 9999999999999X 3 输出例子1: 4 a=input() b=int(input()) #小朋友数量是b n=b #dfs显然超时,尝试用动态规划才是正确的方法.dp[i][j]表示使用字符前i个,除小朋友个数n后余j的个数. dp=[[0]*b for _ in range(len(a)+1)] dp[0][0]=1#表示什么字符都不用,所以i取len(a)就表示用了全部字符 for i in range(1,len(a)+1): for j in range((b)): if a[i-1]=='X': for _ in range((10)): dp[i][(10*j+_)%n]+=dp[i-1][j] else: dp[i][(10*j+int(a[i-1]))%n]+=dp[i-1][j] print(dp[-1][0]) ''' ''' [编程题] 年终奖 时间限制:3秒 空间限制:32768K 小东所在公司要发年终奖,而小东恰好获得了最高福利,他要在公司年会上参与一个抽奖游戏,游戏在一个6*6的棋盘上进行,上面放着36个价值不等的礼物,每个小的棋盘上面放置着一个礼物,他需要从左上角开始游戏,每次只能向下或者向右移动一步,到达右下角停止,一路上的格子里的礼物小东都能拿到,请设计一个算法使小东拿到价值最高的礼物。 给定一个6*6的矩阵board,其中每个元素为对应格子的礼物价值,左上角为[0,0],请返回能获得的最大价值,保证每个礼物价值大于100小于1000。 动规划基本题 ''' ''' [编程题] 小东分苹果 时间限制:3秒 空间限制:32768K 果园里有一堆苹果,一共n头(n大于1小于9)熊来分,第一头为小东,它把苹果均分n份后,多出了一个,它扔掉了这一个,拿走了自己的一份苹果,接着第二头熊重复这一过程,即先均分n份,扔掉一个然后拿走一份,以此类推直到最后一头熊都是这样(最后一头熊扔掉后可以拿走0个,也算是n份均分)。问最初这堆苹果最少有多少个。 给定一个整数n,表示熊的个数,返回最初的苹果数。保证有解。 测试样例: 2 返回:3 #最后的熊拿之前显然有一个苹果,这样最好 倒数第二个熊是,last*(n)/(n-1)+1 # -*- coding:utf-8 -*- class Apples: def getInitial(self, n): # write code here a=n for k in range(99999): out=1+k*a #out表示最后一个熊拿之前的苹果数. for i in range((a-1)): if int(out*a/(a-1))!=out*a/(a-1): break out=out*a//(a-1)+1 else: return out a=Apples() print(a.getInitial(6)) ''' ''' python2 class Apples: def getInitial(self, n): # write code here a=n for k in range(99999): out=1+k*a #out表示最后一个熊拿之前的苹果数. for i in range((a-1)): if int(out*a/(a-1+0.0))!=out*a/(a-1+0.0): break out=out*a/(a-1)+1 else: return out ''' ''' 链接:https://www.nowcoder.com/questionTerminal/532d89889b974506a0805062fd1089fb 来源:牛客网 import java.util.*; /**思路:因为每次分n堆都会多出来1个,所以我们借给熊n-1个,以致每次都可以刚好分成n堆*/ public class Apples { public int getInitial(int n) { long a = (long)Math.pow(n, n); return (int)a-n+1; } } ''' ''' 所以python代码可以写: # -*- coding:utf-8 -*- class Apples: def getInitial(self, n): # write code here return n**n-n++1 ''' ''' 继续做京东的题目: [编程题] 保卫方案 时间限制:2秒 空间限制:65536K 战争游戏的至关重要环节就要到来了,这次的结果将决定王国的生死存亡,小B负责首都的防卫工作。首都位于一个四面环山的盆地中,周围的n个小山构成一个环,作为预警措施,小B计划在每个小山上设置一个观察哨,日夜不停的瞭望周围发生的情况。 一旦发生外地入侵事件,山顶上的岗哨将点燃烽烟,若两个岗哨所在的山峰之间没有更高的山峰遮挡且两者之间有相连通路,则岗哨可以观察到另一个山峰上的烽烟是否点燃。由于小山处于环上,任意两个小山之间存在两个不同的连接通路。满足上述不遮挡的条件下,一座山峰上岗哨点燃的烽烟至少可以通过一条通路被另一端观察到。对于任意相邻的岗哨,一端的岗哨一定可以发现一端点燃的烽烟。 小B设计的这种保卫方案的一个重要特性是能够观测到对方烽烟的岗哨对的数量,她希望你能够帮她解决这个问题。 输入描述: 输入中有多组测试数据,每一组测试数据的第一行为一个整数n(3<=n<=10^6),为首都周围的小山数量,第二行为n个整数,依次表示为小山的高度h(1<=h<=10^9). 输出描述: 对每组测试数据,在单独的一行中输出能相互观察到的岗哨的对数。 输入例子1: 5 1 2 4 5 3 输出例子1: 7 ''' ''' 尽管是一个CS专业的学生,小B的数学基础很好并对数值计算有着特别的兴趣,喜欢用计算机程序来解决数学问题,现在,她正在玩一个数值变换的游戏。她发现计算机中经常用不同的进制表示一个数,如十进制数123表达为16进制时只包含两位数7、11(B),用八进制表示为三位数1、7、3,按不同进制表达时,各个位数的和也不同,如上述例子中十六进制和八进制中各位数的和分别是18和11,。 小B感兴趣的是,一个数A如果按2到A-1进制表达时,各个位数之和的均值是多少?她希望你能帮她解决这个问题? 所有的计算均基于十进制进行,结果也用十进制表示为不可约简的分数形式。 反复算mod就行了 #一个数字按不同进制的各个位加和,反复取mod n=123 def main(n,k): cnt=0 while n!=0: cnt+=n%k #余的数就是我们要的,进制转换算法,就是不停的取mod,算完一个写到最低位. #一直到被除数是0就停止. n=n//k return cnt print(main(123,16)) ''' ''' [编程题] 神奇数 时间限制:1秒 空间限制:32768K 东东在一本古籍上看到有一种神奇数,如果能够将一个数的数字分成两组,其中一组数字的和等于另一组数字的和,我们就将这个数称为神奇数。例如242就是一个神奇数,我们能够将这个数的数字分成两组,分别是{2,2}以及{4},而且这两组数的和都是4.东东现在需要统计给定区间中有多少个神奇数,即给定区间[l, r],统计这个区间中有多少个神奇数,请你来帮助他。 输入描述: 输入包括一行,一行中两个整数l和r(1 ≤ l, r ≤ 10^9, 0 ≤ r - l ≤ 10^6),以空格分割 输出描述: 输出一个整数,即区间内的神奇数个数 输入例子1: 1 50 输出例子1: 4 写一个判断是否是神奇数的函数,然后遍历.这个题目的取值范围写大了.没有1e9这么多 def main(k): save=[] while k!=0: save.append(k%10) k=k//10 # 下面就是判断这个save数组是否能拆成2块和一样的.背包问题 a=sum(save) if a%2==0: half=sum(save)//2 # 是否能拼成half dp =[[0]*(half+1) for _ in range(len(save))] #dp[i][j]表示用到index i,背包空闲为j,最高放的重量 for i in range(len(save)): for j in range((half+1)): if j<save[i]: dp[i][j]=dp[i-1][j] else: dp[i][j]=max(dp[i-1][j],dp[i-1][j-save[i]]+save[i]) return half in dp[-1] else: return False l,r=map(int,input().split()) cnt=0 for i in range(l,r+1): if main(i): cnt+=1 print(cnt) ''' ''' [编程题] 求幂 时间限制:1秒 空间限制:32768K 东东对幂运算很感兴趣,在学习的过程中东东发现了一些有趣的性质: 9^3 = 27^2, 2^10 = 32^2 东东对这个性质充满了好奇,东东现在给出一个整数n,希望你能帮助他求出满足 a^b = c^d(1 ≤ a,b,c,d ≤ n)的式子有多少个。 例如当n = 2: 1^1=1^1 1^1=1^2 1^2=1^1 1^2=1^2 2^1=2^1 2^2=2^2 一共有6个满足要求的式子 输入描述: 输入包括一个整数n(1 ≤ n ≤ 10^6) 输出描述: 输出一个整数,表示满足要求的式子个数。因为答案可能很大,输出对1000000007求模的结果 输入例子1: 2 输出例子1: 6 #为什么这个题目跟公约数有关???? ''' ''' //这个才是正确的代码 作者:牛妹 链接:https://www.nowcoder.com/discuss/38889?type=0&order=3&pos=6&page=1 来源:牛客网 我们考虑去枚举n范围内的所有i,然后处理出i的幂那些数。 这个i就叫做底. 因为a^b=c^d 那么必然存在一个i s.t.下面的十字成立.这个证明做因数分解即可. 考虑对于i ^ x, 我们需要计算满足 (i ^ x) ^ c = (i ^ y) ^ d的数量,其中i ^ x, i ^ y <= n. 这些我们可以通过预处理出来。 然后对于(i ^ x) ^ c = (i ^ y) ^ d 其实意味着x c = y d, 意味着(x / y) = (d / c),(因为c,d可以做到互素) 其中x, y我们可以在预处理之后枚举出来,于是我们就可以借此计算出n范围内有多少不同这种c和d去满足等式。 其实就等于 n / max(x / gcd(x, y), y / gcd(x, y)),然后都累加进答案。gcd()表示最大公约数。 中间可能产生重复枚举,我们用一个set或者hash容器标记一下就好。 以上枚举对于2~sqrt(n)。最后对于大于sqrt(n)的部分,每个的贡献都是n。 import java.util.HashSet; import java.util.Scanner; import java.util.Set; public class Main { public final static long MOD = 1000000000 + 7; public static int max(int a, int b){ return (a>b) ? a : b; } public static long gcd(long a,long b){ return (a % b == 0) ? b : gcd(b,a%b); } public static void main(String[] args) { Scanner in = new Scanner(System.in); long n = in.nextInt(); long ans = (long)1*n*(2*n-1) % MOD;//以1为底的个数,这个计算方式是 1.计算1**x=1**y 有n**2个 2.计算x**y=x**y这个有 n**2-n个 减去这个n表示第一种1里面1为底的已经算过了. //3.所以下面讨论的情况是(i ^ x) ^ c = (i ^ y) ^ d且x!=y且i>1 这种情况.所以i从2取到根号n. Set<Integer> set = new HashSet<>(); for (int i = 2; i*i <= n; i++){ //下面的底至少是2,指数至少也是2,所以i**2<=n if ( set.contains(i)) continue; long tmp = i; int cnt = 0; while(tmp <= n) { set.add((int)tmp); tmp = tmp * i; cnt++; }//比如i取2,n=10的时候,那么set就是{2,4,8} cnt=3,之后4,8就不用算了,因为他们属于2这个底 //cnt表示最高能取多少次幂. for(int k = 1; k <= cnt; k++) { for(int j = k + 1; j <= cnt; j++) { ans = (ans + n / (j / gcd(k, j) ) * (long)2 ) % MOD; //(j / gcd(k, j) )这个操作就是把k,j这个分数变成互素的. //比如k取1,j取2的时候,ans=ans+10/2*2:因为(i ^ x) ^ c = (i ^ y) ^ d且x!=y且i>1 所以这时也就是 (i ^ 1) ^ c = (i ^ 2) ^ d ,那么d最高取5个数分别是1到5,因为c<=10 //又如k=2,j=3, (i ^ 2) ^ c = (i ^ 3) ^ d ,那么d最高取3个分别是2,4,6,因为c<=10 //这个地方为什么这么计算呢因为k,j互素化之后,为了乘积xk=jy,那么x必须是j的倍数,但是x必须小于n //所以x的取法只有n/j种.(这时j已经是(j / gcd(k, j) )了!) } } } System.out.println(ans); } } --------------------- 作者:生命奇迹泉 来源:CSDN 原文:https://blog.csdn.net/shengmingqijiquan/article/details/77899446?utm_source=copy 版权声明:本文为博主原创文章,转载请附上博文链接! ''' ''' sql语句:删除表属于DDL 用的是drop 删除表中数据 是DML 用的是delete 在关系代数运算中,五种基本运算为()。 正确答案: C 你的答案: D (错误) 并、差、选择、投影、自然连接 并、差、交、选择、投影 并、差、选择、投影、乘积 并、差、交、选择、乘积 OSI是开放式系统互连,由ISO制定,按功能可分为物理层、数据链路层、网络层、传输层、会话层、表示层和应用层共七层 在数据库的数据模型中有()。 网状模型、层次模型、关系模型 0-100的N个数(数的值范围为0~100 1 < N <= 1000),分成两组A、B:怎样分|meanA-meanB|最大? 排序后前50一组,后50一组 ''' ''' [编程题] 解码 时间限制:1秒 空间限制:65536K 有一种将字母编码成数字的方式:'a'->1, 'b->2', ... , 'z->26'。 现在给一串数字,给出有多少种可能的译码结果。 输入描述: 编码后数字串 输出描述: 可能的译码结果数 输入例子1: 12 输出例子1: 2 例子说明1: 2种可能的译码结果(”ab” 或”l”) 输入例子2: 31717126241541717 输出例子2: 192 例子说明2: 192种可能的译码结果 a=input() memo={} def main(a):#返回a有多少种编码结果 if a in memo: return memo[a] if a=='0': return 0 if len(a)==0: return 1 if len(a)==1: return 1 tmp=a[:2] hou=a[2:] if int(tmp)==10: return main(hou) if int(tmp)==20: return main(hou) if int(tmp)<27: case1=main(a[1:]) case2=main(a[2:]) memo[a]=case1+case2 return memo[a] else: case1=main(a[1:]) memo[a]=case1 return memo[a] if a=='0': print(0) else: print(main(a)) ''' ''' [编程题] water 时间限制:1秒 空间限制:131072K 给定四个空杯子,容量分别为S1 S2 S3 S4,允许进行以下操作: 1. 将某个杯子接满水 2. 将某个杯子里的水全部倒掉 3. 将杯子A中的水倒进杯子B,直到A倒空或者B被倒满 问最少要多少步操作才能使得这四个杯子装的水分别为T1 T2 T3 T4 输入描述: 第一行四个非负整数S1 S2 S3 S4 第二行四个非负整数T1 T2 T3 T4 输出描述: 最少的步数,若无法完成则输出-1 输入例子1: 0 2 3 4 0 1 2 4 输出例子1: 6 例子说明1: 过程如下: (0,0,0,0)->(0,2,0,0)->(0,2,3,0)->(0,2,0,3)->(0,0,2,3)->(0,2,2,3)->(0,1,2,4) ''' ''' #include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<bitset> using namespace std; bitset<17043521> Hash; const int MAX_STEP = 100000; int WQ[MAX_STEP][6]; int Goal[5]; int Cap[5]; int goalval; int head = 0; int tail = 0; void movw(int numfrom, int numto, int other1, int other2, int other3) { int total = WQ[head][numfrom] + WQ[head][numto]; WQ[tail][other1] = WQ[head][other1]; WQ[tail][other2] = WQ[head][other2]; WQ[tail][other3] = WQ[head][other3]; WQ[tail][5] = WQ[head][5] + 1; if (total>Cap[numto]) { WQ[tail][numfrom] = total - Cap[numto]; WQ[tail][numto] = Cap[numto]; } else { WQ[tail][numfrom] = 0; WQ[tail][numto] = total; } int hashval = WQ[tail][1] * 262144 + WQ[tail][2] * 4096 + WQ[tail][3] * 64 + WQ[tail][4]; if (hashval == goalval) throw WQ[head][5] + 1; if (!Hash[hashval]) { Hash[hashval] = true; if (++tail == MAX_STEP) tail = 0; } } int main() { Hash.reset(); scanf("%d %d %d %d", &Cap[1], &Cap[2], &Cap[3], &Cap[4]); scanf("%d %d %d %d", &Goal[1], &Goal[2], &Goal[3], &Goal[4]); head = 0; tail = 0; goalval = Goal[1] * 262144 + Goal[2] * 4096 + Goal[3] * 64 + Goal[4]; if (Goal[1] == 0 && Goal[2] == 0 && Goal[3] == 0 && Goal[4] == 0) { printf("0"); return 0; } Cap[0] = 6400; WQ[tail][0] = 6400; WQ[tail][1] = 0; WQ[tail][2] = 0; WQ[tail][3] = 0; WQ[tail][4] = 0; WQ[tail][5] = 0; ++tail; try { while (head != tail) { if (WQ[head][0]) { if (Cap[1]) movw(0, 1, 2, 3, 4); if (Cap[2]) movw(0, 2, 1, 3, 4); if (Cap[3]) movw(0, 3, 1, 2, 4); if (Cap[4]) movw(0, 4, 1, 2, 3); } if (WQ[head][1]) { if (Cap[0]) movw(1, 0, 2, 3, 4); if (Cap[2]) movw(1, 2, 0, 3, 4); if (Cap[3]) movw(1, 3, 0, 2, 4); if (Cap[4]) movw(1, 4, 0, 2, 3); } if (WQ[head][2]) { if (Cap[0]) movw(2, 0, 1, 3, 4); if (Cap[1]) movw(2, 1, 0, 3, 4); if (Cap[3]) movw(2, 3, 0, 1, 4); if (Cap[4]) movw(2, 4, 0, 1, 3); } if (WQ[head][3]) { if (Cap[0]) movw(3, 0, 1, 2, 4); if (Cap[1]) movw(3, 1, 0, 2, 4); if (Cap[2]) movw(3, 2, 0, 1, 4); if (Cap[4]) movw(3, 4, 0, 1, 2); } if (WQ[head][4]) { if (Cap[0]) movw(4, 0, 1, 2, 3); if (Cap[1]) movw(4, 1, 0, 2, 3); if (Cap[2]) movw(4, 2, 0, 1, 3); if (Cap[3]) movw(4, 3, 0, 1, 2); } if (++head == MAX_STEP) { head = 0; } } printf("-1"); } catch (int step) { printf("%d ", step); } } ''' ''' #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <bitset> using namespace std; bitset<17043521> Hash; //把ABCD杯子需要的状态抽象为一个值 const int MAX_STEP = 100000; int WQ[MAX_STEP][6];//记录每步操作后0和ABCD的当前容量,最后一个记录操作次数 int Goal[5]; int Cap[5]; int goalval; int head = 0; int tail = 0; void movw(int numfrom, int numto, int other1,int other2,int other3) { int total = WQ[head][numfrom] + WQ[head][numto]; WQ[tail][other1] = WQ[head][other1]; WQ[tail][other2] = WQ[head][other2]; WQ[tail][other3] = WQ[head][other3]; WQ[tail][5] = WQ[head][5] + 1; if (total>Cap[numto]) { WQ[tail][numfrom] = total - Cap[numto]; WQ[tail][numto] = Cap[numto]; } else { WQ[tail][numfrom] = 0; WQ[tail][numto] = total; } int hashval = WQ[tail][1] * 262144 + WQ[tail][2] * 4096 + WQ[tail][3] * 64 + WQ[tail][4]; if (hashval == goalval) throw WQ[head][5] + 1; if (!Hash[hashval])//该次操作之后的状态之前未存在过并记录 { Hash[hashval] = true; if (++tail == MAX_STEP) tail = 0; } } int main() { Hash.reset(); scanf("%d %d %d %d", &Cap[1], &Cap[2], &Cap[3],&Cap[4]); scanf("%d %d %d %d", &Goal[1], &Goal[2], &Goal[3], &Goal[4]); head = 0; tail = 0; goalval = Goal[1] * 262144 + Goal[2] * 4096 + Goal[3]*64+Goal[4]; if (Goal[1] == 0 && Goal[2] == 0 && Goal[3] == 0 && Goal[4] == 0 ) { printf("0"); return 0; } Cap[0] = 6400;//0杯子为足够大的杯子 //初始化0和ABCD杯子当前值 WQ[tail][0] = 6400; WQ[tail][1] = 0; WQ[tail][2] = 0; WQ[tail][3] = 0; WQ[tail][4] = 0; WQ[tail][5] = 0; ++tail; try { while (head != tail) { //A导入B,外层if判断A中当前容量不为零,内层判断B的最大容量不为0 if (WQ[head][0]) { if(Cap[1]) movw(0, 1, 2, 3, 4); if (Cap[2]) movw(0, 2, 1, 3, 4); if (Cap[3]) movw(0, 3, 1, 2, 4); if (Cap[4]) movw(0, 4, 1, 2, 3); } if (WQ[head][1]) { if (Cap[0]) movw(1, 0, 2, 3, 4); if (Cap[2]) movw(1, 2, 0, 3, 4); if (Cap[3]) movw(1, 3, 0, 2, 4); if (Cap[4]) movw(1, 4, 0, 2, 3); } if (WQ[head][2]) { if (Cap[0]) movw(2, 0, 1, 3, 4); if (Cap[1]) movw(2, 1, 0, 3, 4); if (Cap[3]) movw(2, 3, 0, 1, 4); if (Cap[4]) movw(2, 4, 0, 1, 3); } if (WQ[head][3]) { if (Cap[0]) movw(3, 0, 1, 2, 4); if (Cap[1]) movw(3, 1, 0, 2, 4); if (Cap[2]) movw(3, 2, 0, 1, 4); if (Cap[4]) movw(3, 4, 0, 1, 2); } if (WQ[head][4]) { if (Cap[0]) movw(4, 0, 1, 2, 3); if (Cap[1]) movw(4, 1, 0, 2, 3); if (Cap[2]) movw(4, 2, 0, 1, 3); if (Cap[3]) movw(4, 3, 0, 1, 2); } if (++head == MAX_STEP) { head = 0; } } printf("-1"); } catch (int step) { printf("%d ", step); } } ''' ''' 无聊时候可以刷刷 https://www.freecodecamp.cn/ ''' ''' 网易游戏(互娱)-游戏研发/初级游戏研发/平台开发岗部分真题汇总 [编程题] 时钟 时间限制:1秒 空间限制:65536K 注意:本题允许使用C/C++/Java/python进行解答,其他编程语言提交均视作无效处理。 小W有一个电子时钟用于显示时间,显示的格式为HH:MM:SS,HH,MM,SS分别表示时,分,秒。其中时的范围为[‘00’,‘01’…‘23’],分的范围为[‘00’,‘01’…‘59’],秒的范围为[‘00’,‘01’…‘59’]。 #但是有一天小W发现钟表似乎坏了,显示了一个不可能存在的时间“98:23:00”,小W希望改变最少的数字,使得电子时钟显示的时间为一个真实存在的时间,譬如“98:23:00”通过修改第一个’9’为’1’,即可成为一个真实存在的时间“18:23:00”。修改的方法可能有很多,小W想知道,在满足改变最少的数字的前提下,符合条件的字典序最小的时间是多少。其中字典序比较为用“HHMMSS”的6位字符串进行比较。 输入描述: 每个输入数据包含多个测试点。每个测试点后有一个空行。 第一行为测试点的个数T(T<=100)。 每个测试点包含1行,为一个字符串”HH:MM:SS”,表示钟表显示的时间。 输出描述: 对于每个测试点,输出一行。如果钟表显示的时间为真实存在的时间,则不做改动输出该时间,否则输出一个新的”HH:MM:SS”,表示修改最少的数字情况下,字典序最小的真实存在的时间。 输入例子1: 2 19:90:23 23:59:59 输出例子1: 19:00:23 23:59:59 玩字典序的题目. n=int(input()) for i in range(n): str1=input().strip() str2=list(str1) time=str1.split(':') for i in range(len(time)): time[i]=int(time[i]) if time[0]>=24: str2[0]='0' if time[1]>=60: str2[3] = '0' if time[2]>=60: str2[6] = '0' print ("".join(str2)) ''' ''' [编程题] 会话列表 时间限制:1秒 空间限制:32768K 小云正在参与开发一个即时聊天工具,他负责其中的会话列表部分。 会话列表为显示为一个从上到下的多行控件,其中每一行表示一个会话,每一个会话都可以以一个唯一正整数id表示。 当用户在一个会话中发送或接收信息时,如果该会话已经在会话列表中,则会从原来的位置移到列表的最上方;如果没有在会话列表中,则在会话列表最上方插入该会话。 小云在现在要做的工作是测试,他会先把会话列表清空等待接收信息。当接收完大量来自不同会话的信息后,就输出当前的会话列表,以检查其中是否有bug。 输入描述: 输入的第一行为一个正整数T(T<=10),表示测试数据组数。 接下来有T组数据。每组数据的第一行为一个正整数N(1<=N<=200),表示接收到信息的次数。第二行为N个正整数,按时间从先到后的顺序表示接收到信息的会话id。会话id不大于1000000000。 输出描述: 对于每一组数据,输出一行,按会话列表从上到下的顺序,输出会话id。 相邻的会话id以一个空格分隔,行末没有空格。 输入例子1: 3 5 1 2 3 4 5 6 1 100 1000 1000 100 1 7 1 6 3 3 1 8 1 输出例子1: 5 4 3 2 1 1 100 1000 1 8 3 6 num=int(input()) for i in range((num)): a=int(input()) tmp=[int(i)for i in input().split()] out=[] for i in range(len(tmp)): if tmp[i] not in out: out=[tmp[i]]+out else: dex=out.index(tmp[i]) out=[out[dex]]+out[:dex]+out[dex+1:] for i in range(len(out)): out[i]=str(out[i]) print(' '.join(out)) ''' ''' 字符迷阵是一种经典的智力游戏。玩家需要在给定的矩形的字符迷阵中寻找特定的单词。 在这题的规则中,单词是如下规定的: 1. 在字符迷阵中选取一个字符作为单词的开头; 2. 选取右方、下方、或右下45度方向作为单词的延伸方向; 3. 以开头的字符,以选定的延伸方向,把连续得到的若干字符拼接在一起,则称为一个单词。 以图1为例,如果要在其中寻找单词"WORD",则绿色框所标示的都是合法的方案,而红色框所标示的都是不合法的方案。 现在的问题是,给出一个字符迷阵,及一个要寻找的单词,问能在字符迷阵中找到多少个该单词的合法方案。注意合法方案是可以重叠的,如图1所示的字符迷阵,其中单词"WORD"的合法方案有4种。 输入描述: #输入的第一行为一个正整数T,表示测试数据组数。 接下来有T组数据。每组数据的第一行包括两个整数m和n,表示字符迷阵的行数和列数。接下来有m行,每一行为一个长度为n的字符串,按顺序表示每一行之中的字符。再接下来还有一行包括一个字符串,表示要寻找的单词。 数据范围: 对于所有数据,都满足1<=T<=9,且输入的所有位于字符迷阵和单词中的字符都为大写字母。要寻找的单词最短为2个字符,最长为9个字符。字符迷阵和行列数,最小为1,最多为99。 对于其中50%的数据文件,字符迷阵的行列数更限制为最多为20。 输出描述: 对于每一组数据,输出一行,包含一个整数,为在给定的字符迷阵中找到给定的单词的合法方案数。 输入例子1: 3 10 10 AAAAAADROW WORDBBBBBB OCCCWCCCCC RFFFFOFFFF DHHHHHRHHH ZWZVVVVDID ZOZVXXDKIR ZRZVXRXKIO ZDZVOXXKIW ZZZWXXXKIK WORD 3 3 AAA AAA AAA AA 5 8 WORDSWOR ORDSWORD RDSWORDS DSWORDSW SWORDSWO SWORD 输出例子1: 4 16 5 num=int(input()) for i in range((num)): chang,kuan=map(int,input().split()) ditu=[] for h in range((chang)): yihang=[] now=input() for i in now: yihang.append(i) ditu.append(yihang) word=input() #下面就是对于ditu里面找word,经典2维搜索dp问题. #如何写好2维搜索:需要套路!: # 第一步就是构造函数:需要参数至少有chang,kuan,i,j,target,k这5个,必要时候需要一个flag来记录. # 第二部就是判断界线,超界线直接return false#并且写法也是永远不变的 # 第三部是判断target的边界 #第四部直接return 递归 所以前3部边界加最后递归即可. #注意这个题目是一条路走到黑,所以需要些3个函数即可!也算是2维dp的经典题目. def judge1(chang,kuan,i,j,target,k):#棋盘chang*kuan 在位置(i,j)处找是否能拼出target[k:]. if i>=chang or j >=kuan or i<0 or j<0 or ditu[i][j]!=target[k]: return False if k==len(target)-1: return True #以上都是套路模板 return judge1(chang,kuan,i+1,j,target,k+1) def judge2(chang,kuan,i,j,target,k):#棋盘chang*kuan 在位置(i,j)处找是否能拼出target[k:]. if i>=chang or j >=kuan or i<0 or j<0 or ditu[i][j]!=target[k]: return False if k==len(target)-1: return True #以上都是套路模板 return judge2(chang,kuan,i,j+1,target,k+1) def judge3(chang,kuan,i,j,target,k):#棋盘chang*kuan 在位置(i,j)处找是否能拼出target[k:]. if i>=chang or j >=kuan or i<0 or j<0 or ditu[i][j]!=target[k]: return False if k==len(target)-1: return True #以上都是套路模板 return judge3(chang,kuan,i+1,j+1,target,k+1) cnt=0 for i in range((chang)): for j in range((kuan)): if judge1(chang,kuan,i,j,word,0): cnt+=1 if judge2(chang,kuan,i,j,word,0): cnt+=1 if judge3(chang,kuan,i,j,word,0): cnt+=1 print(cnt) 总结:其实写多了这种题目变化很少,套路比较深,对智商要求不高,对编程经验需要比较高而已 10分钟之内搞定,说难题还是那种动态规划类型的题目需要智商高 ''' ''' [编程题] 一封奇怪的信 时间限制:1秒 空间限制:32768K 现在你需要用一台奇怪的打字机书写一封书信。信的每行只能容纳宽度为100的字符,也就是说如果写下某个字符会导致行宽超过100,那么就要另起一行书写 信的内容由a-z的26个小写字母构成,而每个字母的宽度均会事先约定。例如字符宽度约定为[1,2,3,4,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5],那么就代表'a'到'd'四个字母的宽度分别是1,2,3,4,而'e'到'z'的宽度均为5 那么按照上述规则将给定内容S书写成一封信后,这封信共有几行?最后一行宽度是多少? 输入描述: 输入为两行: 第一行是存储了每个字符宽度的字符串,包含26个数字,以1个空格分隔,每个数字均小于等于10 第二行是存储了待输入字符的字符串S,字符串S的长度在1到1000之间 输出描述: 输出为信的行数以及最后一行所包含的字符个数,中间以1个空格分隔 输入例子1: 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 helloworld 输出例子1: 1 50 例子说明1: "5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5"规定每个字符宽度为5 "helloworld"是输入的字符串S 由于S共包含10个字符,也即共占用50个字符宽度,因此可以写在同一行 输入例子2: 5 5 5 5 5 5 10 10 10 10 10 10 10 10 10 10 10 10 5 5 5 5 5 5 5 5 hahahahahahahaha 输出例子2: 2 20 例子说明2: "5 5 5 5 5 5 10 10 10 10 10 10 10 10 10 10 10 10 5 5 5 5 5 5 5 5"规定了每个字符宽度 "hahahahahahahaha"是输入的字符串S 由于h宽度为10,a宽度为5,因此'hahahahahahah'占用100字符宽度可以写在第一行,‘aha’写在第二行也即最后一行。因此字符宽度为20 典型的计算机模拟过程的题目,意义不大. ''' ''' [编程题] 糖果谜题 时间限制:1秒 空间限制:32768K 小明是幼儿园的一名老师。某天幼儿园园长给小朋友们每人发一颗糖果,小朋友们拿到后发现有一些同学拿到的糖果颜色和自己相同,有一些同学糖果颜色和自己不同。 假定每个小朋友只知道有多少同学和自己拿到了相同颜色的糖果。 上课后,有一部分小朋友兴奋的把这一结果告诉小明老师,并让小明老师猜一猜,最少有多少同学拿到了糖果。 例如有三个小朋友告诉小明老师这一结果如下: 其中第一个小朋友发现有1人和自己糖果颜色一样,第二个小朋友也发现有1人和自己糖果颜色一样,第三个小朋友发现有3人和自己糖果颜色一样。 第一二个小朋友可互相认为对方和自己颜色相同,比如红色; 第三个小朋友不可能再为红色(否则第一二个小朋友会发现有2人和自己糖果颜色相同),假设他拿到的为蓝色糖果,那么至少还有另外3位同学拿到蓝色的糖果,最终至少有6位小朋友拿到了糖果。 现在请你帮助小明老师解答下这个谜题。 输入描述: 假定部分小朋友的回答用空格间隔,如 1 1 3 输出描述: 直接打印最少有多少位小朋友拿到糖果 如 6 输入例子1: 1 1 3 输出例子1: 6 输入例子2: 0 0 0 输出例子2: 3 例子说明2: 三位小朋友都没发现有人和自己的颜色相同,所以最少的情况就是三位小朋友糖果的颜色均不同 也就是相同数字合并.来判断. tmp=[int(i)for i in input().split()] a=set(tmp) suoyouren=0 for i in a: #比如有5个2那么,每一个2只能跟2个其他2进行配对,所以需要 suoyouren+=(tmp.count(i)+i)//(i+1)*(i+1) #太帅了,居然一下过! print(suoyouren) 还是讲一下思路,就是小朋友配对问题.里面也用到了分宿舍技巧. 比如有5个小朋友多说看到2个人跟自己颜色相同,那么我们需要每3个小朋友分配一个颜色,这样最省颜色,也就达到了小朋友的利用率最高,也就让小朋友的数量最少. 那么5个小朋友,每3个分配一个颜色,还剩下2个小鹏有,但是他们也说看到2个颜色,所以要把5个2补成6个2的情况就可以了.就是这一行:(tmp.count(i)+i)//(i+1)*(i+1) ''' ''' [编程题] 字符串编码 时间限制:1秒 空间限制:32768K 给定一个字符串,请你将字符串重新编码,将连续的字符替换成“连续出现的个数+字符”。比如字符串AAAABCCDAA会被编码成4A1B2C1D2A。 输入描述: 每个测试输入包含1个测试用例 每个测试用例输入只有一行字符串,字符串只包括大写英文字母,长度不超过10000。 输出描述: 输出编码后的字符串 输入例子1: AAAABCCDAA 输出例子1: 4A1B2C1D2A 感觉就是单纯考编程技术而已.设置2个指针,一个start一个now.然后不一样就now-start计数即可. ''' ''' [编程题] 最大和 时间限制:1秒 空间限制:32768K 在一个N*N的数组中寻找所有横,竖,左上到右下,右上到左下,四种方向的直线连续D个数字的和里面最大的值 输入描述: 每个测试输入包含1个测试用例,第一行包括两个整数 N 和 D : 3 <= N <= 100 1 <= D <= N 接下来有N行,每行N个数字d: 0 <= d <= 100 输出描述: 输出一个整数,表示找到的和的最大值 输入例子1: 4 2 87 98 79 61 10 27 95 70 20 64 73 29 71 65 15 0 输出例子1: 193 也就是98+98=193 #也是2维搜索问题 n,d=map(int,input().split()) ditu=[] chang=n kuan=n for i in range((n)): tmp=[int(i)for i in input().split()] ditu.append(tmp) def qiuhe1(chang,kuan,i,j,step):#沿着横着走step步能得到的和 #上来就写边界条件: if i>chang-1 or j>kuan-1 or i<0 or j<0 or step==0: return -float('inf')#因为题目不要长度不够的数!!!!!!!!所以设置负无穷即可. if step==1: return ditu[i][j] return ditu[i][j]+qiuhe1(chang,kuan,i,j+1,step-1) def qiuhe2(chang,kuan,i,j,step):#沿着横着走step步能得到的和 #上来就写边界条件: if i>chang-1 or j>kuan-1 or i<0 or j<0 or step==0: return -float('inf') if step==1: return ditu[i][j] return ditu[i][j]+qiuhe2(chang,kuan,i+1,j,step-1) def qiuhe3(chang,kuan,i,j,step):#沿着横着走step步能得到的和 #上来就写边界条件: if i>chang-1 or j>kuan-1 or i<0 or j<0 or step==0: return -float('inf') if step==1: return ditu[i][j] return ditu[i][j]+qiuhe3(chang,kuan,i+1,j+1,step-1) def qiuhe4(chang,kuan,i,j,step):#沿着横着走step步能得到的和 #上来就写边界条件: if i>chang-1 or j>kuan-1 or i<0 or j<0 or step==0: return -float('inf') if step==1: return ditu[i][j] return ditu[i][j]+qiuhe4(chang,kuan,i+1,j-1,step-1) maxi=0 for i in range((chang)): for j in range((kuan)): maxi=max(maxi,qiuhe1(chang,kuan,i,j,d),qiuhe2(chang,kuan,i,j,d),qiuhe3(chang,kuan,i,j,d),qiuhe4(chang,kuan,i,j,d)) print(maxi) ''' ''' [编程题] 推箱子 时间限制:1秒 空间限制:32768K 大家一定玩过“推箱子”这个经典的游戏。具体规则就是在一个N*M的地图上,有1个玩家、1个箱子、1个目的地以及若干障碍,其余是空地。玩家可以往上下左右4个方向移动,但是不能移动出地图或者移动到障碍里去。如果往这个方向移动推到了箱子,箱子也会按这个方向移动一格,当然,箱子也不能被推出地图或推到障碍里。当箱子被推到目的地以后,游戏目标达成。现在告诉你游戏开始是初始的地图布局,请你求出玩家最少需要移动多少步才能够将游戏目标达成。 输入描述: 每个测试输入包含1个测试用例 第一行输入两个数字N,M表示地图的大小。其中0<N,M<=8。 接下来有N行,每行包含M个字符表示该行地图。其中 . 表示空地、X表示玩家、*表示箱子、#表示障碍、@表示目的地。 每个地图必定包含1个玩家、1个箱子、1个目的地。 输出描述: 输出一个数字表示玩家最少需要移动多少步才能将游戏目标达成。当无论如何达成不了的时候,输出-1。 输入例子1: 4 4 .... ..*@ .... .X.. 6 6 ...#.. ...... #*##.. ..##.# ..X... .@#... 输出例子1: 3 11 ''' ''' [编程题] 赛马 时间限制:1秒 空间限制:32768K 在一条无限长的跑道上,有N匹马在不同的位置上出发开始赛马。当开始赛马比赛后,所有的马开始以自己的速度一直匀速前进。每匹马的速度都不一样,且全部是同样的均匀随机分布。在比赛中当某匹马追上了前面的某匹马时,被追上的马就出局。 请问按以上的规则比赛无限长的时间后,赛道上剩余的马匹数量的数学期望是多少 输入描述: 每个测试输入包含1个测试用例 输入只有一行,一个正整数N 1 <= N <= 1000 输出描述: 输出一个浮点数,精确到小数点后四位数字,表示剩余马匹数量的数学期望 输入例子1: 1 2 输出例子1: 1.0000 1.5000 #看看数学上如何分析的,第i快的马货到最后概率是1/i+1 把马的速度设置为0到1之间的实数. 1.看每个马对于最后期望的贡献是多少? 2.最快的马显然是1 3.第二块的马,那么假设他的位置距离原点是x.初始位置是0到1的实数, 那么只有当最快的马在他前面他才能贡献期望1,否则贡献0.所以是(1-x)从0到1做积分.得到1/2 4........类似分析即可答案是调和级数. n = int(raw_input()) res = 0 for i in range(n): res += 1.0/(i+1) print r"%.4f" %res ''' ''' 倒水问题:这个题目的版本非常之多,有微软版的,腾讯版的,新浪版的等等,最常见的是给你一个容量为5升的桶和一个容量为3升的桶,水不限使用,要求精确得到4升水。 倒2次就完事了. [问题]有两个容桶,小桶的容量是4升,大桶的容量是9升,怎样才能从河中恰好打上6升水呢? 先大桶中弄好1升,然后给小桶,之后大桶从9开始给小桶即可. ''' ''' 为了解决倒水问题:先从基础抓起: 倒水问题 总时间限制: 1000ms 内存限制: 65536kB 描述 有三个分别容量分别为a升、b升和c升的杯子(a>b>c>0,且b与c互质)。 a杯装满水,b与c均为空。 三个筒相互倒水且不准把水倒往三个筒之外。 请用最少的倒水次数,倒出d升水(任一杯中正好水量为d 即可),并输出倒水的过程。 输入 只有一行:a、b、c、d 四个整数。 输出 第一行为倒水过程的总步骤 N ,其后N行为倒水的过程; 若无解,则输出“No find”。 样例输入 10 7 3 4 样例输出 3 10 0 0 3 7 0 3 4 3 明显的广搜,这里把vector、queue、stack都用了一遍 --------------------- 作者:zjc_617445 来源:CSDN 原文:https://blog.csdn.net/hsfz_zjc/article/details/75005668 版权声明:本文为博主原创文章,转载请附上博文链接! #include <cstdio> #include <queue> #include <stack> #include <vector> #include <algorithm> #include <iostream> #include <cstdlib> using namespace std; //结构体 struct node { int v[3]; int f; }; //全局变量 const int maxn=200+5; int a,b,c,d; bool tf[maxn][maxn]; int cap[3]; vector <node> vec; bool isok(int i) //判断是否倒水已经成功 { return vec[i].v[0]==d||vec[i].v[1]==d||vec[i].v[2]==d; } void out(int i) { int j; stack<int> sta; do { sta.push(i); if(vec[i].f!=i) i=vec[i].f; else break; }while(1) ; printf("%d ",sta.size() ); while(!sta.empty()) { j=sta.top() ;sta.pop() ; printf("%d %d %d ",vec[j].v[0],vec[j].v[1],vec[j].v[2]); } } void work(int a,int b,int c,int d) { //初始化 for(int i=0;i<maxn;i++) for(int j=0;j<maxn;j++) tf[i][j]=false; vec.clear() ; //准备 queue<int> que; int curr,ii; cap[0]=a; cap[1]=b; cap[2]=c; node s; if(a<d) { printf("No find");return; } s.v[0]=a;s.v[1]=0;s.v[2]=0;s.f =0; vec.push_back(s); if(isok(0)) { printf("1 %d 0 0",a);return; } tf[a][0]=true; que.push(0); //开始 while(!que.empty()) { curr=que.front(); que.pop() ; for(int i=0;i<3;i++) for(int j=0;j<3;j++) { //i->j // printf("** "); if(i==j||vec[curr].v[i]==0||vec[curr].v[j]==cap[j]) continue; // printf("44 "); ii=min(cap[j]-vec[curr].v[j],vec[curr].v[i]); s.f =curr; for(int o=0;o<3;o++) s.v [o]=vec[curr].v[o]; s.v[i]-=ii; s.v[j]+=ii; if(!tf[s.v[0]][s.v[1]]) { tf[s.v[0]][s.v[1]]=true; vec.push_back(s); if(isok(vec.size()-1)) { out(vec.size()-1); return; } que.push(vec.size() -1) ; } } } printf("No find"); } int main() { scanf("%d%d%d%d",&a,&b,&c,&d); work(a,b,c,d); return 0; } ''' ''' 题目要求 有两个容器,容积分别为A升和B升,有无限多的水,现在需要C升水。 我们还有一个足够大的水缸,足够容纳C升水。起初它是空的,我们只能往水缸里倒入水,而不能倒出。 可以进行的操作是: 把一个容器灌满; 把一个容器清空(容器里剩余的水全部倒掉,或者倒入水缸); 用一个容器的水倒入另外一个容器,直到倒出水的容器空或者倒入水的容器满。 问是否能够通过有限次操作,使得水缸最后恰好有C升水。 输入:三个整数A, B, C,其中 0 < A , B, C <= 1000000000 输出:0或1,表示能否达到要求。 函数头部: c语言:1表示可以,0表示不可以 int can(int a,int b,int c); c++语言: true表示可以,false表示不可以 bool can(int a,int b,int c); java语言:true表示可以,false表示不可以 public class Main { public static boolean can(int a,int b,int c); } 解题思路 自己分析: 比如按照大小顺序是a,b 那么可以拼出(ax-by) 这个恰好是最大公约数的公式,所以知道最大公约数可以被拼出来.从而公约数的倍数也是一样表达, 所以一样可以拼出来.那么需要证明的是不是最大公约数的倍数一定拼不出来! 证明:从倒水过程可以看出来能拼出来的数,算上倒掉的水.总体一定是ax+by.因为每一次加水都是加a或者加b,(因为杯子没有刻度).那么每一次倒掉的水也一定是a或者b的倍数.所以最后剩下的水也是ax+by. 所以显然是最大公约数的倍数.所以判断一个target是否能倒出来,只需要判断他是否是最大公钥数的倍数即可. 这是一个典型的倒水问题/量水问题,使用欧几里得算法就可解出来。 这里有一篇文章给出了简单的倒水问题的解法,可以解决笔试面试里面一些简单的填空题,可以看一看:http://blog.csdn.net/morewindows/article/details/7481851 基本思想是:不断用小桶装水倒入大桶,大桶满了立即清空,每次判断下二个桶中水的容量是否等于指定容量。也就是用小桶容量的倍数对大桶的容量进行取余,直到余数等于指定容量。 例如,用7升的桶和11升的桶得到2升水可以这样做: 7 % 11 = 7 14 % 11 = 3 21 % 11 = 10 28 % 11 = 6 35 % 11 = 2 成功得到2升水。 对于明确说明可以得到xx升水,需要我们给出如何倒出来的步骤,可以用这个方法,很快捷。但是这个方法不适合解这道题。 欧几里德算法又称辗转相除法,用于计算两个正整数a,b的最大公约数。 用gcd(a,b) 表示a, b的最大公约数,则有定理:gcd(a,b) = gcd(b,a mod b) (a>b 且a mod b 不为0) 具体的算法实现有循环和递归两种,我用的是循环的方法。 扩展欧几里得算法 定理:对于不完全为 0 的非负整数 a,b,gcd(a, b)表示 a, b 的最大公约数,必然存在整数对 x, y ,使得 gcd(a,b)=ax+by。 本题实际上是问是否存在整数x, y,使得ax+by=c成立。如果c可以被gcd(a,b)整除,则成立。 因此解题步骤如下: 1. 求出gcd(a,b) 2. 判断c是否能被gcd(a,b)整除,若能则返回true,否则返回false ''' ''' dfs:倒水 这个题目看起来好像是一道模拟题,其实不然,这是一道dfs搜索题,只不过看起来好像无从下手,其实想想就好了,我们可以用一个vis数组来保存当前的状态如果之前某一次倒水出现过这种情况,我们就无需再次去遍历这种情况,只需要遍历其他情况就好了,还有一个重要的剪枝就是假如说我们已经找到某一种情况可以到达目标状态,那么深度再深的我们就无需再次去遍历,因为绝对不是最优解。 --------------------- 作者:caojiangxia 来源:CSDN 原文:https://blog.csdn.net/caojiangxia/article/details/46341005 版权声明:本文为博主原创文章,转载请附上博文链接! 抄点歌曲 [原][歌曲]感动的歌曲排序 故事: 起风了 买辣椒也用券 《起风了》情感历程 成长: 木马城市 毛不易 男孩长大为人 感悟: 在人间 王建房 爱情: 你还要我怎样 薛之谦 分手后的怀念 非常非常精彩的dp问题!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 理解了一点dp的本质就是函数递归,写好函数,然后递归调用.期间用动态规划. 注意flag的使用,和递归出来一般需要flag归位!!!!!!!!!! #include<cstdio> #include<cstring> int a,b,c,t,vis[105][105];//题目:用a,b两个杯子如何倒出c这么多的水 //t表示深度,如果深度大于t就停止dp char s[205][15],s2[205][15],choice[][10]={"FILL(1)","FILL(2)","DROP(1)","DROP(2)","POUR(1,2)","POUR(2,1)"}; void dfs(int n,int m,int deep){ int dn,dm,i,j; if(deep>=t) return; //如果其中一个水杯已经满足有c单位的水就成功,所以这时候就让全局变量t设置为deep if(n==c||m==c){ t=deep; for(i=0;i<t;i++) strcpy(s2[i],s[i]);//把s的所有操作都给s2,作为保存 } //下面是6种操作分类讨论. strcpy(s[deep],choice[0]); if(!vis[a][m]){//因为操作0是fill(1),所以得到的结果是第一个杯子满了是a,第二个杯子是m vis[a][m]=1;//表示进入 dfs(a,m,deep+1);//出来递归的时候,把这个flag再变回去,所以下面一行再设置为未访问. //非常牛逼的思路.当然比较朴素,但是我就是dp垃圾,感觉还是8皇后问题理解不够.自己想不到dp思路. vis[a][m]=0; } // strcpy(s[deep],choice[1]); if(!vis[n][b]){ vis[n][b]=1; dfs(n,b,deep+1); vis[n][b]=0;//递归出来一般需要flag归位!!!!!!!!!! } strcpy(s[deep],choice[2]); if(!vis[0][m]){ vis[0][m]=1; dfs(0,m,deep+1); vis[0][m]=0; } strcpy(s[deep],choice[3]); if(!vis[n][0]){ vis[n][0]=1; dfs(n,0,deep+1); vis[n][0]=0; } strcpy(s[deep],choice[4]); if(b-m>=n){ dn=0; dm=m+n; } else { dn=n-(b-m); dm=b; } if(!vis[dn][dm]){ vis[dn][dm]=1; dfs(dn,dm,deep+1); vis[dn][dm]=0; } strcpy(s[deep],choice[5]); if(a-n>=m){ dm=0; dn=m+n; }//不够倒满第一个杯子,所以第一个杯子m+n第二杯0 else { dm=m-(a-n); dn=a; }//够倒满所以第一个杯子a,第二个杯子m-a+n if(!vis[dn][dm]){ vis[dn][dm]=1; dfs(dn,dm,deep+1); vis[dn][dm]=0; } } int main(void){ int i; while(scanf("%d %d %d",&a,&b,&c)!=EOF){ t=1000000000; memset(vis,0,sizeof(vis)); dfs(0,0,0); if(t==1000000000) printf("impossible "); else{ printf("%d ",t); for(i=0;i<t;i++) printf("%s ",s2[i]); } } } '''
继续保存:包含挺多dp题目.2018-10-23,10点34 虽然拿到秋招offer,但是还是会继续把牛客网的笔试题目做完.

#下面这一段用一个txt来保存input的信息来模拟input.最后提交代码时候删除这一段即可. a9999=open('1.txt','r') def input(): return a9999.readline().rstrip(' ') #输入数据的一些模板 # n,a=map(int,input().split()) # arr=[int(i)for i in input().split()] # 格式化输出 # print('%.2f'%(maxi/2)) ''' # 最大公约数用 import fractions fractions.gcd(a,b) #多个分隔符: import re b=re.split('[+*-]',a) ''' ''' [编程题] 魔力手环 时间限制:1秒 空间限制:32768K 小易拥有一个拥有魔力的手环上面有n个数字(构成一个环),当这个魔力手环每次使用魔力的时候就会发生一种奇特的变化:每个数字会变成自己跟后面一个数字的和(最后一个数字的后面一个数字是第一个),一旦某个位置的数字大于等于100就马上对100取模(比如某个位置变为103,就会自动变为3).现在给出这个魔力手环的构成,请你计算出使用k次魔力之后魔力手环的状态。 输入描述: 输入数据包括两行: 第一行为两个整数n(2 ≤ n ≤ 50)和k(1 ≤ k ≤ 2000000000),以空格分隔 第二行为魔力手环初始的n个数,以空格分隔。范围都在0至99. 输出描述: 输出魔力手环使用k次之后的状态,以空格分隔,行末无空格。 输入例子1: 3 2 1 2 3 输出例子1: 8 9 7 Python3(3.5.2)重置自测 1 先找规律: 比如3个数: a,b,c turn1: a+b b+c c+a turn2: a+2b+c b+2c+a c+2a+b turn3: 2a+3b+3c 2b+3c+3a 2c+3a+3b turn4: 5a+5b+6c 5b+6a+5c 5c+5a+6b #只能这样了,应该是因为python3的速度太慢了 #看了网友的答案,原来这种高效率递归问题用矩阵幂来解决. #(a1,....an)=(a1,....an)(x1,...xn) 就是对角线和次对焦都是1的矩阵. #矩阵高次幂用算2次.....2^n次拼起来即可. n,k=map(int,input().split())#题目k取2e11 arr=[int(i)for i in input().split()] def multi(a,b):#a,b是同介方阵 c=[[0]*len(a)for _ in range(len(a))] #注意二维矩阵的写法,外层不要写乘因为list的mute属性问题!!!!!!! for i in range(len(a)): for j in range(len(a)): for k in range(len(a)): c[i][j]+=a[i][k]*b[k][j] c[i][j]%=100 return (c) matrix=[[0]*len(arr)for _ in range (len(arr))] #变换矩阵 matrix[0][0]=1 matrix[0][len(matrix)-1]=1 for i in range(1,len(matrix)): matrix[i][i]=1 matrix[i][i-1]=1 def multiK(mat,k):#求矩阵mat的k次幂,这个算法需要熟悉理解 danwei=[[0]*len(mat)for _ in range(len(mat))] for i in range(len(danwei)): danwei[i][i]=1 out=danwei #这里用单位矩阵来出事话 while k : if k&1==1:#当k的2进制最后一位是1,那么输出就乘一下mat,然后mat自平方,k>>1 out = multi(out,mat) mat = multi(mat,mat) k = k>>1 else: mat = multi(mat,mat) k = k>>1 return out #下面把arr跟multiK(matrix,k)乘一下,注意行列 out=[0]*len(matrix) for i in range(len(matrix)): for j in range(len(matrix)): out[i]+=arr[j]*multiK(matrix,k)[j][i] out[i]%=100 for i in range(len(out)): out[i]=str(out[i]) print(' '.join(out)) 提交运行 提前交卷下一题 收藏本题 标记一下 提交结果有问题? 收起答题卡 ''' ''' # [编程题] 工作安排 # 时间限制:1秒 # 空间限制:32768K # 现在有n位工程师和6项工作(编号为0至5),现在给出每个人能够胜任的工作序号表(用一个字符串表示,比如:045,表示某位工程师能够胜任0号,4号,5号工作)。现在需要进行工作安排,每位工程师只能被安排到自己能够胜任的工作当中去,两位工程师不能安排到同一项工作当中去。如果两种工作安排中有一个人被安排在的工作序号不一样就被视为不同的工作安排,现在需要计算出有多少种不同工作安排计划。 输入描述: 输入数据有n+1行: 第一行为工程师人数n(1 ≤ n ≤ 6) 接下来的n行,每行一个字符串表示第i(1 ≤ i ≤ n)个人能够胜任的工作(字符串不一定等长的) 输出描述: 输出一个整数,表示有多少种不同的工作安排方案 输入例子1: 6 012345 012345 012345 012345 012345 012345 输出例子1: 720 n=int(input()) arr=[input() for _ in range(n)] left=range(6) def main(dex,left):#返回剩余工作left,给dex拍工作 这个数量. cnt=0 if dex==n-1: tmp=[str(i) for i in left] a=0 for i in tmp: if i in arr[dex]: a+=1 return a for i in range(len(left)): if str(left[i]) in arr[dex]: now=left[:] now=list(now) now.pop(i) cnt+=main(dex+1,now) return cnt if left==[]: print(0) else: print(main(0,left)) ''' ''' [编程题] 集合 时间限制:1秒 空间限制:32768K 小易最近在数学课上学习到了集合的概念,集合有三个特征:1.确定性 2.互异性 3.无序性. 小易的老师给了小易这样一个集合: S = { p/q | w ≤ p ≤ x, y ≤ q ≤ z } 需要根据给定的w,x,y,z,求出集合中一共有多少个元素。小易才学习了集合还解决不了这个复杂的问题,需要你来帮助他。 输入描述: 输入包括一行: 一共4个整数分别是w(1 ≤ w ≤ x),x(1 ≤ x ≤ 100),y(1 ≤ y ≤ z),z(1 ≤ z ≤ 100).以空格分隔 输出描述: 输出集合中元素的个数 输入例子1: 1 10 1 1 输出例子1: 10 w,x,y,z=map(int,input().split()) a=set([]) for i in range(w,x+1): for j in range(y,z+1): a.add(i/j) print(len(a)) ''' ''' [编程题] 奇怪的表达式求值 时间限制:1秒 空间限制:32768K 常规的表达式求值,我们都会根据计算的优先级来计算。比如*/的优先级就高于+-。但是小易所生活的世界的表达式规则很简单,从左往右依次计算即可,而且小易所在的世界没有除法,意味着表达式中没有/,只有(+, - 和 *)。现在给出一个表达式,需要你帮忙计算出小易所在的世界这个表达式的值为多少 输入描述: 输入为一行字符串,即一个表达式。其中运算符只有-,+,*。参与计算的数字只有0~9. 保证表达式都是合法的,排列规则如样例所示。 输出描述: 输出一个数,即表达式的值 输入例子1: 3+5*7 输出例子1: 56 a=input() import re b=re.split('[+*-]',a) fuhao=[] for i in range(len(a)): if a[i] in '+-*': fuhao.append(a[i]) while len(b)!=1: tmp=b[0]+fuhao[0]+b[1] fuhao.pop(0) b=[str(eval(tmp))]+b[2:] print(b[0]) ''' ''' 编程题] 涂棋盘 时间限制:1秒 空间限制:32768K 小易有一块n*n的棋盘,棋盘的每一个格子都为黑色或者白色,小易现在要用他喜欢的红色去涂画棋盘。小易会找出棋盘中某一列中拥有相同颜色的最大的区域去涂画,帮助小易算算他会涂画多少个棋格。 输入描述: 输入数据包括n+1行: 第一行为一个整数n(1 ≤ n ≤ 50),即棋盘的大小 接下来的n行每行一个字符串表示第i行棋盘的颜色,'W'表示白色,'B'表示黑色 输出描述: 输出小易会涂画的区域大小 输入例子1: 3 BWW BBB BWB 输出例子1: 3 a=int(input()) b=[] for i in range((a)): tmp=input() base=[] for i in tmp: base.append(i) b.append(base) #不用numpy实现矩阵转至 tmp=[] for i in range(len(b)): save=[] for j in range(len(b)): save.append(b[j][i]) tmp.append(save) memo=[] for i in tmp: maxi=0 cnt=1 for j in range(1,len(i)): if i[j]==i[j-1]: cnt+=1 maxi=max(maxi,cnt) else: maxi=max(maxi,cnt) cnt=1 memo.append(maxi) print(max(memo)) ''' ''' [编程题] 小易记单词 时间限制:1秒 空间限制:32768K 小易参与了一个记单词的小游戏。游戏开始系统提供了m个不同的单词,小易记忆一段时间之后需要在纸上写出他记住的单词。小易一共写出了n个他能记住的单词,如果小易写出的单词是在系统提供的,将获得这个单词长度的平方的分数。注意小易写出的单词可能重复,但是对于每个正确的单词只能计分一次。 输入描述: 输入数据包括三行: 第一行为两个整数n(1 ≤ n ≤ 50)和m(1 ≤ m ≤ 50)。以空格分隔 第二行为n个字符串,表示小易能记住的单词,以空格分隔,每个单词的长度小于等于50。 第三行为m个字符串,系统提供的单词,以空格分隔,每个单词的长度小于等于50。 输出描述: 输出一个整数表示小易能获得的分数 输入例子1: 3 4 apple orange strawberry strawberry orange grapefruit watermelon 输出例子1: 136 n,m=map(int,input().split()) jiyi=input().split()[:n] #这个题目有bug这里面他给的多了,所以需要些:n来切片即可. xitong=input().split()[:m] jiyi=set(jiyi) xitong=set(xitong) cnt=0 for i in jiyi: if i in xitong: cnt+=len(i)**2 print(cnt) ''' ''' [编程题] 堆砖块 时间限制:1秒 空间限制:32768K 小易有n块砖块,每一块砖块有一个高度。小易希望利用这些砖块堆砌两座相同高度的塔。为了让问题简单,砖块堆砌就是简单的高度相加,某一块砖只能使用在一座塔中一次。小易现在让能够堆砌出来的两座塔的高度尽量高,小易能否完成呢。 输入描述: 输入包括两行: 第一行为整数n(1 ≤ n ≤ 50),即一共有n块砖块 第二行为n个整数,表示每一块砖块的高度height[i] (1 ≤ height[i] ≤ 500000) 输出描述: 如果小易能堆砌出两座高度相同的塔,输出最高能拼凑的高度,如果不能则输出-1. 保证答案不大于500000。 输入例子1: 3 2 3 5 输出例子1: 5 这个题目动态规划还可以.是相当可以了,非常难.因为他的递归不是按照index,而是按照高度差 ''' ''' 别人的java答案:非常牛逼: 链接:https://www.nowcoder.com/questionTerminal/040924ba0e64423b8a3fe2f75a56934a 来源:牛客网 /** 思路来自于csdn上,大概看了一次,这次是完全凭记忆写出来的,主要的就是利用动态规划的思想, dp[i][j]表示在使用前i块砖,高度差为j时低塔的高度,考虑四种情况: 1. 新砖块放在低塔上,:低塔依然是低塔,即 dp[i][j] = dp[i-1][j+high] + high; 2. 新砖块放在低塔上,低塔变成了高塔,即: dp[i][j] = dp[i-1][high-j] + high-j; 3. 新砖块放在高塔上,高塔只可能是高塔,即: dp[i][j] = dp[i-1][j-high]; 4. 放弃新砖块,不放在任何一个塔上,即: dp[i][j] = dp[i-1][j]; 最终dp[i][j]取以上四种情况的最大值即可; 如果直接定义n*sum维的数组,内存会不够,所以优化了一下内存,应该有更好的方法,再学习了 */ import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); while (sc.hasNext()) { int n = sc.nextInt(); int[] h = new int[n]; int sum = 0; for (int i = 0; i < n; i++) { h[i] = sc.nextInt(); sum += h[i]; } //sum表示所有砖块的总和 int[][] dp = new int[2][sum+1]; //dp[i][j] 定义2 是因为利用滚动数组,表示前i个砖块中,堆成的塔,高度差为j时,低塔的最高高度 所以最后需要返回i是n,j为0的时候的解即可. for (int i = 0; i < 2; i++) { for (int j = 0; j < sum + 1; j++) { dp[i][j] = Integer.MIN_VALUE; //初始化为负无穷,表示没有这种高度的堆法 } } dp[0][0] = 0; //如果没有放砖的时候,低塔为0,高度差为0 for (int i = 0; i < n; i++) { int high = h[i]; //比如放第二个砖块之前,high就是第一个砖块????????这个地方不理解 //核心就是下面4行代码! for (int j = 0; j <= sum; j++) { //非常精彩的4个推理!!!!!!!!!!!!!!!!!!!!!!!!!!!!! if(j > high) { //如果将砖块放在高塔上,则低塔高度不变,高度差增加 //之前的差是j-high,现在的高是j,high表示当前需要插入的砖的高度 dp[1][j] = Math.max(dp[1][j], dp[0][j - high]); } else {//如果当前插入砖的高度>=j //如果将砖块放在低塔上,低塔变高塔,高塔高度变低塔高度,高度差改变 dp[1][j] = Math.max(dp[1][j], dp[0][high - j] + (high - j)); } //如果将新砖块放在低塔上,并且依然是低塔,则低塔高度增加 if(j + high <= sum) dp[1][j] = Math.max(dp[1][j], dp[0][j + high] + high); //放弃该砖块,不放在任何一个塔上 dp[1][j] = Math.max(dp[1][j], dp[0][j]); } System.arraycopy(dp[1], 0, dp[0], 0, sum + 1);//交换数组的数据,所以不管数据n是多少,最后的数据总是在dp[0]里面. for (int j = 0; j <= sum; j++) { dp[1][0] = Integer.MIN_VALUE; } } if(dp[0][0] > 0) System.out.println(dp[0][0]); else System.out.println(-1); } } } ''' ''' [编程题] 分饼干 时间限制:1秒 空间限制:32768K 易老师购买了一盒饼干,盒子中一共有k块饼干,但是数字k有些数位变得模糊了,看不清楚数字具体是多少了。易老师需要你帮忙把这k块饼干平分给n个小朋友,易老师保证这盒饼干能平分给n个小朋友。现在你需要计算出k有多少种可能的数值 输入描述: 输入包括两行: 第一行为盒子上的数值k,模糊的数位用X表示,长度小于18(可能有多个模糊的数位) 第二行为小朋友的人数n 输出描述: 输出k可能的数值种数,保证至少为1 输入例子1: 9999999999999X 3 输出例子1: 4 a=input() b=int(input()) #小朋友数量是b n=b #dfs显然超时,尝试用动态规划才是正确的方法.dp[i][j]表示使用字符前i个,除小朋友个数n后余j的个数. dp=[[0]*b for _ in range(len(a)+1)] dp[0][0]=1#表示什么字符都不用,所以i取len(a)就表示用了全部字符 for i in range(1,len(a)+1): for j in range((b)): if a[i-1]=='X': for _ in range((10)): dp[i][(10*j+_)%n]+=dp[i-1][j] else: dp[i][(10*j+int(a[i-1]))%n]+=dp[i-1][j] print(dp[-1][0]) ''' ''' [编程题] 年终奖 时间限制:3秒 空间限制:32768K 小东所在公司要发年终奖,而小东恰好获得了最高福利,他要在公司年会上参与一个抽奖游戏,游戏在一个6*6的棋盘上进行,上面放着36个价值不等的礼物,每个小的棋盘上面放置着一个礼物,他需要从左上角开始游戏,每次只能向下或者向右移动一步,到达右下角停止,一路上的格子里的礼物小东都能拿到,请设计一个算法使小东拿到价值最高的礼物。 给定一个6*6的矩阵board,其中每个元素为对应格子的礼物价值,左上角为[0,0],请返回能获得的最大价值,保证每个礼物价值大于100小于1000。 动规划基本题 ''' ''' [编程题] 小东分苹果 时间限制:3秒 空间限制:32768K 果园里有一堆苹果,一共n头(n大于1小于9)熊来分,第一头为小东,它把苹果均分n份后,多出了一个,它扔掉了这一个,拿走了自己的一份苹果,接着第二头熊重复这一过程,即先均分n份,扔掉一个然后拿走一份,以此类推直到最后一头熊都是这样(最后一头熊扔掉后可以拿走0个,也算是n份均分)。问最初这堆苹果最少有多少个。 给定一个整数n,表示熊的个数,返回最初的苹果数。保证有解。 测试样例: 2 返回:3 #最后的熊拿之前显然有一个苹果,这样最好 倒数第二个熊是,last*(n)/(n-1)+1 # -*- coding:utf-8 -*- class Apples: def getInitial(self, n): # write code here a=n for k in range(99999): out=1+k*a #out表示最后一个熊拿之前的苹果数. for i in range((a-1)): if int(out*a/(a-1))!=out*a/(a-1): break out=out*a//(a-1)+1 else: return out a=Apples() print(a.getInitial(6)) ''' ''' python2 class Apples: def getInitial(self, n): # write code here a=n for k in range(99999): out=1+k*a #out表示最后一个熊拿之前的苹果数. for i in range((a-1)): if int(out*a/(a-1+0.0))!=out*a/(a-1+0.0): break out=out*a/(a-1)+1 else: return out ''' ''' 链接:https://www.nowcoder.com/questionTerminal/532d89889b974506a0805062fd1089fb 来源:牛客网 import java.util.*; /**思路:因为每次分n堆都会多出来1个,所以我们借给熊n-1个,以致每次都可以刚好分成n堆*/ public class Apples { public int getInitial(int n) { long a = (long)Math.pow(n, n); return (int)a-n+1; } } ''' ''' 所以python代码可以写: # -*- coding:utf-8 -*- class Apples: def getInitial(self, n): # write code here return n**n-n++1 ''' ''' 继续做京东的题目: [编程题] 保卫方案 时间限制:2秒 空间限制:65536K 战争游戏的至关重要环节就要到来了,这次的结果将决定王国的生死存亡,小B负责首都的防卫工作。首都位于一个四面环山的盆地中,周围的n个小山构成一个环,作为预警措施,小B计划在每个小山上设置一个观察哨,日夜不停的瞭望周围发生的情况。 一旦发生外地入侵事件,山顶上的岗哨将点燃烽烟,若两个岗哨所在的山峰之间没有更高的山峰遮挡且两者之间有相连通路,则岗哨可以观察到另一个山峰上的烽烟是否点燃。由于小山处于环上,任意两个小山之间存在两个不同的连接通路。满足上述不遮挡的条件下,一座山峰上岗哨点燃的烽烟至少可以通过一条通路被另一端观察到。对于任意相邻的岗哨,一端的岗哨一定可以发现一端点燃的烽烟。 小B设计的这种保卫方案的一个重要特性是能够观测到对方烽烟的岗哨对的数量,她希望你能够帮她解决这个问题。 输入描述: 输入中有多组测试数据,每一组测试数据的第一行为一个整数n(3<=n<=10^6),为首都周围的小山数量,第二行为n个整数,依次表示为小山的高度h(1<=h<=10^9). 输出描述: 对每组测试数据,在单独的一行中输出能相互观察到的岗哨的对数。 输入例子1: 5 1 2 4 5 3 输出例子1: 7 ''' ''' 尽管是一个CS专业的学生,小B的数学基础很好并对数值计算有着特别的兴趣,喜欢用计算机程序来解决数学问题,现在,她正在玩一个数值变换的游戏。她发现计算机中经常用不同的进制表示一个数,如十进制数123表达为16进制时只包含两位数7、11(B),用八进制表示为三位数1、7、3,按不同进制表达时,各个位数的和也不同,如上述例子中十六进制和八进制中各位数的和分别是18和11,。 小B感兴趣的是,一个数A如果按2到A-1进制表达时,各个位数之和的均值是多少?她希望你能帮她解决这个问题? 所有的计算均基于十进制进行,结果也用十进制表示为不可约简的分数形式。 反复算mod就行了 #一个数字按不同进制的各个位加和,反复取mod n=123 def main(n,k): cnt=0 while n!=0: cnt+=n%k #余的数就是我们要的,进制转换算法,就是不停的取mod,算完一个写到最低位. #一直到被除数是0就停止. n=n//k return cnt print(main(123,16)) ''' ''' [编程题] 神奇数 时间限制:1秒 空间限制:32768K 东东在一本古籍上看到有一种神奇数,如果能够将一个数的数字分成两组,其中一组数字的和等于另一组数字的和,我们就将这个数称为神奇数。例如242就是一个神奇数,我们能够将这个数的数字分成两组,分别是{2,2}以及{4},而且这两组数的和都是4.东东现在需要统计给定区间中有多少个神奇数,即给定区间[l, r],统计这个区间中有多少个神奇数,请你来帮助他。 输入描述: 输入包括一行,一行中两个整数l和r(1 ≤ l, r ≤ 10^9, 0 ≤ r - l ≤ 10^6),以空格分割 输出描述: 输出一个整数,即区间内的神奇数个数 输入例子1: 1 50 输出例子1: 4 写一个判断是否是神奇数的函数,然后遍历.这个题目的取值范围写大了.没有1e9这么多 def main(k): save=[] while k!=0: save.append(k%10) k=k//10 # 下面就是判断这个save数组是否能拆成2块和一样的.背包问题 a=sum(save) if a%2==0: half=sum(save)//2 # 是否能拼成half dp =[[0]*(half+1) for _ in range(len(save))] #dp[i][j]表示用到index i,背包空闲为j,最高放的重量 for i in range(len(save)): for j in range((half+1)): if j<save[i]: dp[i][j]=dp[i-1][j] else: dp[i][j]=max(dp[i-1][j],dp[i-1][j-save[i]]+save[i]) return half in dp[-1] else: return False l,r=map(int,input().split()) cnt=0 for i in range(l,r+1): if main(i): cnt+=1 print(cnt) ''' ''' [编程题] 求幂 时间限制:1秒 空间限制:32768K 东东对幂运算很感兴趣,在学习的过程中东东发现了一些有趣的性质: 9^3 = 27^2, 2^10 = 32^2 东东对这个性质充满了好奇,东东现在给出一个整数n,希望你能帮助他求出满足 a^b = c^d(1 ≤ a,b,c,d ≤ n)的式子有多少个。 例如当n = 2: 1^1=1^1 1^1=1^2 1^2=1^1 1^2=1^2 2^1=2^1 2^2=2^2 一共有6个满足要求的式子 输入描述: 输入包括一个整数n(1 ≤ n ≤ 10^6) 输出描述: 输出一个整数,表示满足要求的式子个数。因为答案可能很大,输出对1000000007求模的结果 输入例子1: 2 输出例子1: 6 #为什么这个题目跟公约数有关???? ''' ''' //这个才是正确的代码 作者:牛妹 链接:https://www.nowcoder.com/discuss/38889?type=0&order=3&pos=6&page=1 来源:牛客网 我们考虑去枚举n范围内的所有i,然后处理出i的幂那些数。 这个i就叫做底. 因为a^b=c^d 那么必然存在一个i s.t.下面的十字成立.这个证明做因数分解即可. 考虑对于i ^ x, 我们需要计算满足 (i ^ x) ^ c = (i ^ y) ^ d的数量,其中i ^ x, i ^ y <= n. 这些我们可以通过预处理出来。 然后对于(i ^ x) ^ c = (i ^ y) ^ d 其实意味着x c = y d, 意味着(x / y) = (d / c),(因为c,d可以做到互素) 其中x, y我们可以在预处理之后枚举出来,于是我们就可以借此计算出n范围内有多少不同这种c和d去满足等式。 其实就等于 n / max(x / gcd(x, y), y / gcd(x, y)),然后都累加进答案。gcd()表示最大公约数。 中间可能产生重复枚举,我们用一个set或者hash容器标记一下就好。 以上枚举对于2~sqrt(n)。最后对于大于sqrt(n)的部分,每个的贡献都是n。 import java.util.HashSet; import java.util.Scanner; import java.util.Set; public class Main { public final static long MOD = 1000000000 + 7; public static int max(int a, int b){ return (a>b) ? a : b; } public static long gcd(long a,long b){ return (a % b == 0) ? b : gcd(b,a%b); } public static void main(String[] args) { Scanner in = new Scanner(System.in); long n = in.nextInt(); long ans = (long)1*n*(2*n-1) % MOD;//以1为底的个数,这个计算方式是 1.计算1**x=1**y 有n**2个 2.计算x**y=x**y这个有 n**2-n个 减去这个n表示第一种1里面1为底的已经算过了. //3.所以下面讨论的情况是(i ^ x) ^ c = (i ^ y) ^ d且x!=y且i>1 这种情况.所以i从2取到根号n. Set<Integer> set = new HashSet<>(); for (int i = 2; i*i <= n; i++){ //下面的底至少是2,指数至少也是2,所以i**2<=n if ( set.contains(i)) continue; long tmp = i; int cnt = 0; while(tmp <= n) { set.add((int)tmp); tmp = tmp * i; cnt++; }//比如i取2,n=10的时候,那么set就是{2,4,8} cnt=3,之后4,8就不用算了,因为他们属于2这个底 //cnt表示最高能取多少次幂. for(int k = 1; k <= cnt; k++) { for(int j = k + 1; j <= cnt; j++) { ans = (ans + n / (j / gcd(k, j) ) * (long)2 ) % MOD; //(j / gcd(k, j) )这个操作就是把k,j这个分数变成互素的. //比如k取1,j取2的时候,ans=ans+10/2*2:因为(i ^ x) ^ c = (i ^ y) ^ d且x!=y且i>1 所以这时也就是 (i ^ 1) ^ c = (i ^ 2) ^ d ,那么d最高取5个数分别是1到5,因为c<=10 //又如k=2,j=3, (i ^ 2) ^ c = (i ^ 3) ^ d ,那么d最高取3个分别是2,4,6,因为c<=10 //这个地方为什么这么计算呢因为k,j互素化之后,为了乘积xk=jy,那么x必须是j的倍数,但是x必须小于n //所以x的取法只有n/j种.(这时j已经是(j / gcd(k, j) )了!) } } } System.out.println(ans); } } --------------------- 作者:生命奇迹泉 来源:CSDN 原文:https://blog.csdn.net/shengmingqijiquan/article/details/77899446?utm_source=copy 版权声明:本文为博主原创文章,转载请附上博文链接! ''' ''' sql语句:删除表属于DDL 用的是drop 删除表中数据 是DML 用的是delete 在关系代数运算中,五种基本运算为()。 正确答案: C 你的答案: D (错误) 并、差、选择、投影、自然连接 并、差、交、选择、投影 并、差、选择、投影、乘积 并、差、交、选择、乘积 OSI是开放式系统互连,由ISO制定,按功能可分为物理层、数据链路层、网络层、传输层、会话层、表示层和应用层共七层 在数据库的数据模型中有()。 网状模型、层次模型、关系模型 0-100的N个数(数的值范围为0~100 1 < N <= 1000),分成两组A、B:怎样分|meanA-meanB|最大? 排序后前50一组,后50一组 ''' ''' [编程题] 解码 时间限制:1秒 空间限制:65536K 有一种将字母编码成数字的方式:'a'->1, 'b->2', ... , 'z->26'。 现在给一串数字,给出有多少种可能的译码结果。 输入描述: 编码后数字串 输出描述: 可能的译码结果数 输入例子1: 12 输出例子1: 2 例子说明1: 2种可能的译码结果(”ab” 或”l”) 输入例子2: 31717126241541717 输出例子2: 192 例子说明2: 192种可能的译码结果 a=input() memo={} def main(a):#返回a有多少种编码结果 if a in memo: return memo[a] if a=='0': return 0 if len(a)==0: return 1 if len(a)==1: return 1 tmp=a[:2] hou=a[2:] if int(tmp)==10: return main(hou) if int(tmp)==20: return main(hou) if int(tmp)<27: case1=main(a[1:]) case2=main(a[2:]) memo[a]=case1+case2 return memo[a] else: case1=main(a[1:]) memo[a]=case1 return memo[a] if a=='0': print(0) else: print(main(a)) ''' ''' [编程题] water 时间限制:1秒 空间限制:131072K 给定四个空杯子,容量分别为S1 S2 S3 S4,允许进行以下操作: 1. 将某个杯子接满水 2. 将某个杯子里的水全部倒掉 3. 将杯子A中的水倒进杯子B,直到A倒空或者B被倒满 问最少要多少步操作才能使得这四个杯子装的水分别为T1 T2 T3 T4 输入描述: 第一行四个非负整数S1 S2 S3 S4 第二行四个非负整数T1 T2 T3 T4 输出描述: 最少的步数,若无法完成则输出-1 输入例子1: 0 2 3 4 0 1 2 4 输出例子1: 6 例子说明1: 过程如下: (0,0,0,0)->(0,2,0,0)->(0,2,3,0)->(0,2,0,3)->(0,0,2,3)->(0,2,2,3)->(0,1,2,4) ''' ''' #include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<bitset> using namespace std; bitset<17043521> Hash; const int MAX_STEP = 100000; int WQ[MAX_STEP][6]; int Goal[5]; int Cap[5]; int goalval; int head = 0; int tail = 0; void movw(int numfrom, int numto, int other1, int other2, int other3) { int total = WQ[head][numfrom] + WQ[head][numto]; WQ[tail][other1] = WQ[head][other1]; WQ[tail][other2] = WQ[head][other2]; WQ[tail][other3] = WQ[head][other3]; WQ[tail][5] = WQ[head][5] + 1; if (total>Cap[numto]) { WQ[tail][numfrom] = total - Cap[numto]; WQ[tail][numto] = Cap[numto]; } else { WQ[tail][numfrom] = 0; WQ[tail][numto] = total; } int hashval = WQ[tail][1] * 262144 + WQ[tail][2] * 4096 + WQ[tail][3] * 64 + WQ[tail][4]; if (hashval == goalval) throw WQ[head][5] + 1; if (!Hash[hashval]) { Hash[hashval] = true; if (++tail == MAX_STEP) tail = 0; } } int main() { Hash.reset(); scanf("%d %d %d %d", &Cap[1], &Cap[2], &Cap[3], &Cap[4]); scanf("%d %d %d %d", &Goal[1], &Goal[2], &Goal[3], &Goal[4]); head = 0; tail = 0; goalval = Goal[1] * 262144 + Goal[2] * 4096 + Goal[3] * 64 + Goal[4]; if (Goal[1] == 0 && Goal[2] == 0 && Goal[3] == 0 && Goal[4] == 0) { printf("0"); return 0; } Cap[0] = 6400; WQ[tail][0] = 6400; WQ[tail][1] = 0; WQ[tail][2] = 0; WQ[tail][3] = 0; WQ[tail][4] = 0; WQ[tail][5] = 0; ++tail; try { while (head != tail) { if (WQ[head][0]) { if (Cap[1]) movw(0, 1, 2, 3, 4); if (Cap[2]) movw(0, 2, 1, 3, 4); if (Cap[3]) movw(0, 3, 1, 2, 4); if (Cap[4]) movw(0, 4, 1, 2, 3); } if (WQ[head][1]) { if (Cap[0]) movw(1, 0, 2, 3, 4); if (Cap[2]) movw(1, 2, 0, 3, 4); if (Cap[3]) movw(1, 3, 0, 2, 4); if (Cap[4]) movw(1, 4, 0, 2, 3); } if (WQ[head][2]) { if (Cap[0]) movw(2, 0, 1, 3, 4); if (Cap[1]) movw(2, 1, 0, 3, 4); if (Cap[3]) movw(2, 3, 0, 1, 4); if (Cap[4]) movw(2, 4, 0, 1, 3); } if (WQ[head][3]) { if (Cap[0]) movw(3, 0, 1, 2, 4); if (Cap[1]) movw(3, 1, 0, 2, 4); if (Cap[2]) movw(3, 2, 0, 1, 4); if (Cap[4]) movw(3, 4, 0, 1, 2); } if (WQ[head][4]) { if (Cap[0]) movw(4, 0, 1, 2, 3); if (Cap[1]) movw(4, 1, 0, 2, 3); if (Cap[2]) movw(4, 2, 0, 1, 3); if (Cap[3]) movw(4, 3, 0, 1, 2); } if (++head == MAX_STEP) { head = 0; } } printf("-1"); } catch (int step) { printf("%d ", step); } } ''' ''' #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <bitset> using namespace std; bitset<17043521> Hash; //把ABCD杯子需要的状态抽象为一个值 const int MAX_STEP = 100000; int WQ[MAX_STEP][6];//记录每步操作后0和ABCD的当前容量,最后一个记录操作次数 int Goal[5]; int Cap[5]; int goalval; int head = 0; int tail = 0; void movw(int numfrom, int numto, int other1,int other2,int other3) { int total = WQ[head][numfrom] + WQ[head][numto]; WQ[tail][other1] = WQ[head][other1]; WQ[tail][other2] = WQ[head][other2]; WQ[tail][other3] = WQ[head][other3]; WQ[tail][5] = WQ[head][5] + 1; if (total>Cap[numto]) { WQ[tail][numfrom] = total - Cap[numto]; WQ[tail][numto] = Cap[numto]; } else { WQ[tail][numfrom] = 0; WQ[tail][numto] = total; } int hashval = WQ[tail][1] * 262144 + WQ[tail][2] * 4096 + WQ[tail][3] * 64 + WQ[tail][4]; if (hashval == goalval) throw WQ[head][5] + 1; if (!Hash[hashval])//该次操作之后的状态之前未存在过并记录 { Hash[hashval] = true; if (++tail == MAX_STEP) tail = 0; } } int main() { Hash.reset(); scanf("%d %d %d %d", &Cap[1], &Cap[2], &Cap[3],&Cap[4]); scanf("%d %d %d %d", &Goal[1], &Goal[2], &Goal[3], &Goal[4]); head = 0; tail = 0; goalval = Goal[1] * 262144 + Goal[2] * 4096 + Goal[3]*64+Goal[4]; if (Goal[1] == 0 && Goal[2] == 0 && Goal[3] == 0 && Goal[4] == 0 ) { printf("0"); return 0; } Cap[0] = 6400;//0杯子为足够大的杯子 //初始化0和ABCD杯子当前值 WQ[tail][0] = 6400; WQ[tail][1] = 0; WQ[tail][2] = 0; WQ[tail][3] = 0; WQ[tail][4] = 0; WQ[tail][5] = 0; ++tail; try { while (head != tail) { //A导入B,外层if判断A中当前容量不为零,内层判断B的最大容量不为0 if (WQ[head][0]) { if(Cap[1]) movw(0, 1, 2, 3, 4); if (Cap[2]) movw(0, 2, 1, 3, 4); if (Cap[3]) movw(0, 3, 1, 2, 4); if (Cap[4]) movw(0, 4, 1, 2, 3); } if (WQ[head][1]) { if (Cap[0]) movw(1, 0, 2, 3, 4); if (Cap[2]) movw(1, 2, 0, 3, 4); if (Cap[3]) movw(1, 3, 0, 2, 4); if (Cap[4]) movw(1, 4, 0, 2, 3); } if (WQ[head][2]) { if (Cap[0]) movw(2, 0, 1, 3, 4); if (Cap[1]) movw(2, 1, 0, 3, 4); if (Cap[3]) movw(2, 3, 0, 1, 4); if (Cap[4]) movw(2, 4, 0, 1, 3); } if (WQ[head][3]) { if (Cap[0]) movw(3, 0, 1, 2, 4); if (Cap[1]) movw(3, 1, 0, 2, 4); if (Cap[2]) movw(3, 2, 0, 1, 4); if (Cap[4]) movw(3, 4, 0, 1, 2); } if (WQ[head][4]) { if (Cap[0]) movw(4, 0, 1, 2, 3); if (Cap[1]) movw(4, 1, 0, 2, 3); if (Cap[2]) movw(4, 2, 0, 1, 3); if (Cap[3]) movw(4, 3, 0, 1, 2); } if (++head == MAX_STEP) { head = 0; } } printf("-1"); } catch (int step) { printf("%d ", step); } } ''' ''' 无聊时候可以刷刷 https://www.freecodecamp.cn/ ''' ''' 网易游戏(互娱)-游戏研发/初级游戏研发/平台开发岗部分真题汇总 [编程题] 时钟 时间限制:1秒 空间限制:65536K 注意:本题允许使用C/C++/Java/python进行解答,其他编程语言提交均视作无效处理。 小W有一个电子时钟用于显示时间,显示的格式为HH:MM:SS,HH,MM,SS分别表示时,分,秒。其中时的范围为[‘00’,‘01’…‘23’],分的范围为[‘00’,‘01’…‘59’],秒的范围为[‘00’,‘01’…‘59’]。 #但是有一天小W发现钟表似乎坏了,显示了一个不可能存在的时间“98:23:00”,小W希望改变最少的数字,使得电子时钟显示的时间为一个真实存在的时间,譬如“98:23:00”通过修改第一个’9’为’1’,即可成为一个真实存在的时间“18:23:00”。修改的方法可能有很多,小W想知道,在满足改变最少的数字的前提下,符合条件的字典序最小的时间是多少。其中字典序比较为用“HHMMSS”的6位字符串进行比较。 输入描述: 每个输入数据包含多个测试点。每个测试点后有一个空行。 第一行为测试点的个数T(T<=100)。 每个测试点包含1行,为一个字符串”HH:MM:SS”,表示钟表显示的时间。 输出描述: 对于每个测试点,输出一行。如果钟表显示的时间为真实存在的时间,则不做改动输出该时间,否则输出一个新的”HH:MM:SS”,表示修改最少的数字情况下,字典序最小的真实存在的时间。 输入例子1: 2 19:90:23 23:59:59 输出例子1: 19:00:23 23:59:59 玩字典序的题目. n=int(input()) for i in range(n): str1=input().strip() str2=list(str1) time=str1.split(':') for i in range(len(time)): time[i]=int(time[i]) if time[0]>=24: str2[0]='0' if time[1]>=60: str2[3] = '0' if time[2]>=60: str2[6] = '0' print ("".join(str2)) ''' ''' [编程题] 会话列表 时间限制:1秒 空间限制:32768K 小云正在参与开发一个即时聊天工具,他负责其中的会话列表部分。 会话列表为显示为一个从上到下的多行控件,其中每一行表示一个会话,每一个会话都可以以一个唯一正整数id表示。 当用户在一个会话中发送或接收信息时,如果该会话已经在会话列表中,则会从原来的位置移到列表的最上方;如果没有在会话列表中,则在会话列表最上方插入该会话。 小云在现在要做的工作是测试,他会先把会话列表清空等待接收信息。当接收完大量来自不同会话的信息后,就输出当前的会话列表,以检查其中是否有bug。 输入描述: 输入的第一行为一个正整数T(T<=10),表示测试数据组数。 接下来有T组数据。每组数据的第一行为一个正整数N(1<=N<=200),表示接收到信息的次数。第二行为N个正整数,按时间从先到后的顺序表示接收到信息的会话id。会话id不大于1000000000。 输出描述: 对于每一组数据,输出一行,按会话列表从上到下的顺序,输出会话id。 相邻的会话id以一个空格分隔,行末没有空格。 输入例子1: 3 5 1 2 3 4 5 6 1 100 1000 1000 100 1 7 1 6 3 3 1 8 1 输出例子1: 5 4 3 2 1 1 100 1000 1 8 3 6 num=int(input()) for i in range((num)): a=int(input()) tmp=[int(i)for i in input().split()] out=[] for i in range(len(tmp)): if tmp[i] not in out: out=[tmp[i]]+out else: dex=out.index(tmp[i]) out=[out[dex]]+out[:dex]+out[dex+1:] for i in range(len(out)): out[i]=str(out[i]) print(' '.join(out)) ''' ''' 字符迷阵是一种经典的智力游戏。玩家需要在给定的矩形的字符迷阵中寻找特定的单词。 在这题的规则中,单词是如下规定的: 1. 在字符迷阵中选取一个字符作为单词的开头; 2. 选取右方、下方、或右下45度方向作为单词的延伸方向; 3. 以开头的字符,以选定的延伸方向,把连续得到的若干字符拼接在一起,则称为一个单词。 以图1为例,如果要在其中寻找单词"WORD",则绿色框所标示的都是合法的方案,而红色框所标示的都是不合法的方案。 现在的问题是,给出一个字符迷阵,及一个要寻找的单词,问能在字符迷阵中找到多少个该单词的合法方案。注意合法方案是可以重叠的,如图1所示的字符迷阵,其中单词"WORD"的合法方案有4种。 输入描述: #输入的第一行为一个正整数T,表示测试数据组数。 接下来有T组数据。每组数据的第一行包括两个整数m和n,表示字符迷阵的行数和列数。接下来有m行,每一行为一个长度为n的字符串,按顺序表示每一行之中的字符。再接下来还有一行包括一个字符串,表示要寻找的单词。 数据范围: 对于所有数据,都满足1<=T<=9,且输入的所有位于字符迷阵和单词中的字符都为大写字母。要寻找的单词最短为2个字符,最长为9个字符。字符迷阵和行列数,最小为1,最多为99。 对于其中50%的数据文件,字符迷阵的行列数更限制为最多为20。 输出描述: 对于每一组数据,输出一行,包含一个整数,为在给定的字符迷阵中找到给定的单词的合法方案数。 输入例子1: 3 10 10 AAAAAADROW WORDBBBBBB OCCCWCCCCC RFFFFOFFFF DHHHHHRHHH ZWZVVVVDID ZOZVXXDKIR ZRZVXRXKIO ZDZVOXXKIW ZZZWXXXKIK WORD 3 3 AAA AAA AAA AA 5 8 WORDSWOR ORDSWORD RDSWORDS DSWORDSW SWORDSWO SWORD 输出例子1: 4 16 5 num=int(input()) for i in range((num)): chang,kuan=map(int,input().split()) ditu=[] for h in range((chang)): yihang=[] now=input() for i in now: yihang.append(i) ditu.append(yihang) word=input() #下面就是对于ditu里面找word,经典2维搜索dp问题. #如何写好2维搜索:需要套路!: # 第一步就是构造函数:需要参数至少有chang,kuan,i,j,target,k这5个,必要时候需要一个flag来记录. # 第二部就是判断界线,超界线直接return false#并且写法也是永远不变的 # 第三部是判断target的边界 #第四部直接return 递归 所以前3部边界加最后递归即可. #注意这个题目是一条路走到黑,所以需要些3个函数即可!也算是2维dp的经典题目. def judge1(chang,kuan,i,j,target,k):#棋盘chang*kuan 在位置(i,j)处找是否能拼出target[k:]. if i>=chang or j >=kuan or i<0 or j<0 or ditu[i][j]!=target[k]: return False if k==len(target)-1: return True #以上都是套路模板 return judge1(chang,kuan,i+1,j,target,k+1) def judge2(chang,kuan,i,j,target,k):#棋盘chang*kuan 在位置(i,j)处找是否能拼出target[k:]. if i>=chang or j >=kuan or i<0 or j<0 or ditu[i][j]!=target[k]: return False if k==len(target)-1: return True #以上都是套路模板 return judge2(chang,kuan,i,j+1,target,k+1) def judge3(chang,kuan,i,j,target,k):#棋盘chang*kuan 在位置(i,j)处找是否能拼出target[k:]. if i>=chang or j >=kuan or i<0 or j<0 or ditu[i][j]!=target[k]: return False if k==len(target)-1: return True #以上都是套路模板 return judge3(chang,kuan,i+1,j+1,target,k+1) cnt=0 for i in range((chang)): for j in range((kuan)): if judge1(chang,kuan,i,j,word,0): cnt+=1 if judge2(chang,kuan,i,j,word,0): cnt+=1 if judge3(chang,kuan,i,j,word,0): cnt+=1 print(cnt) 总结:其实写多了这种题目变化很少,套路比较深,对智商要求不高,对编程经验需要比较高而已 10分钟之内搞定,说难题还是那种动态规划类型的题目需要智商高 ''' ''' [编程题] 一封奇怪的信 时间限制:1秒 空间限制:32768K 现在你需要用一台奇怪的打字机书写一封书信。信的每行只能容纳宽度为100的字符,也就是说如果写下某个字符会导致行宽超过100,那么就要另起一行书写 信的内容由a-z的26个小写字母构成,而每个字母的宽度均会事先约定。例如字符宽度约定为[1,2,3,4,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5],那么就代表'a'到'd'四个字母的宽度分别是1,2,3,4,而'e'到'z'的宽度均为5 那么按照上述规则将给定内容S书写成一封信后,这封信共有几行?最后一行宽度是多少? 输入描述: 输入为两行: 第一行是存储了每个字符宽度的字符串,包含26个数字,以1个空格分隔,每个数字均小于等于10 第二行是存储了待输入字符的字符串S,字符串S的长度在1到1000之间 输出描述: 输出为信的行数以及最后一行所包含的字符个数,中间以1个空格分隔 输入例子1: 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 helloworld 输出例子1: 1 50 例子说明1: "5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5"规定每个字符宽度为5 "helloworld"是输入的字符串S 由于S共包含10个字符,也即共占用50个字符宽度,因此可以写在同一行 输入例子2: 5 5 5 5 5 5 10 10 10 10 10 10 10 10 10 10 10 10 5 5 5 5 5 5 5 5 hahahahahahahaha 输出例子2: 2 20 例子说明2: "5 5 5 5 5 5 10 10 10 10 10 10 10 10 10 10 10 10 5 5 5 5 5 5 5 5"规定了每个字符宽度 "hahahahahahahaha"是输入的字符串S 由于h宽度为10,a宽度为5,因此'hahahahahahah'占用100字符宽度可以写在第一行,‘aha’写在第二行也即最后一行。因此字符宽度为20 典型的计算机模拟过程的题目,意义不大. ''' ''' [编程题] 糖果谜题 时间限制:1秒 空间限制:32768K 小明是幼儿园的一名老师。某天幼儿园园长给小朋友们每人发一颗糖果,小朋友们拿到后发现有一些同学拿到的糖果颜色和自己相同,有一些同学糖果颜色和自己不同。 假定每个小朋友只知道有多少同学和自己拿到了相同颜色的糖果。 上课后,有一部分小朋友兴奋的把这一结果告诉小明老师,并让小明老师猜一猜,最少有多少同学拿到了糖果。 例如有三个小朋友告诉小明老师这一结果如下: 其中第一个小朋友发现有1人和自己糖果颜色一样,第二个小朋友也发现有1人和自己糖果颜色一样,第三个小朋友发现有3人和自己糖果颜色一样。 第一二个小朋友可互相认为对方和自己颜色相同,比如红色; 第三个小朋友不可能再为红色(否则第一二个小朋友会发现有2人和自己糖果颜色相同),假设他拿到的为蓝色糖果,那么至少还有另外3位同学拿到蓝色的糖果,最终至少有6位小朋友拿到了糖果。 现在请你帮助小明老师解答下这个谜题。 输入描述: 假定部分小朋友的回答用空格间隔,如 1 1 3 输出描述: 直接打印最少有多少位小朋友拿到糖果 如 6 输入例子1: 1 1 3 输出例子1: 6 输入例子2: 0 0 0 输出例子2: 3 例子说明2: 三位小朋友都没发现有人和自己的颜色相同,所以最少的情况就是三位小朋友糖果的颜色均不同 也就是相同数字合并.来判断. tmp=[int(i)for i in input().split()] a=set(tmp) suoyouren=0 for i in a: #比如有5个2那么,每一个2只能跟2个其他2进行配对,所以需要 suoyouren+=(tmp.count(i)+i)//(i+1)*(i+1) #太帅了,居然一下过! print(suoyouren) 还是讲一下思路,就是小朋友配对问题.里面也用到了分宿舍技巧. 比如有5个小朋友多说看到2个人跟自己颜色相同,那么我们需要每3个小朋友分配一个颜色,这样最省颜色,也就达到了小朋友的利用率最高,也就让小朋友的数量最少. 那么5个小朋友,每3个分配一个颜色,还剩下2个小鹏有,但是他们也说看到2个颜色,所以要把5个2补成6个2的情况就可以了.就是这一行:(tmp.count(i)+i)//(i+1)*(i+1) ''' ''' [编程题] 字符串编码 时间限制:1秒 空间限制:32768K 给定一个字符串,请你将字符串重新编码,将连续的字符替换成“连续出现的个数+字符”。比如字符串AAAABCCDAA会被编码成4A1B2C1D2A。 输入描述: 每个测试输入包含1个测试用例 每个测试用例输入只有一行字符串,字符串只包括大写英文字母,长度不超过10000。 输出描述: 输出编码后的字符串 输入例子1: AAAABCCDAA 输出例子1: 4A1B2C1D2A 感觉就是单纯考编程技术而已.设置2个指针,一个start一个now.然后不一样就now-start计数即可. ''' ''' [编程题] 最大和 时间限制:1秒 空间限制:32768K 在一个N*N的数组中寻找所有横,竖,左上到右下,右上到左下,四种方向的直线连续D个数字的和里面最大的值 输入描述: 每个测试输入包含1个测试用例,第一行包括两个整数 N 和 D : 3 <= N <= 100 1 <= D <= N 接下来有N行,每行N个数字d: 0 <= d <= 100 输出描述: 输出一个整数,表示找到的和的最大值 输入例子1: 4 2 87 98 79 61 10 27 95 70 20 64 73 29 71 65 15 0 输出例子1: 193 也就是98+98=193 #也是2维搜索问题 n,d=map(int,input().split()) ditu=[] chang=n kuan=n for i in range((n)): tmp=[int(i)for i in input().split()] ditu.append(tmp) def qiuhe1(chang,kuan,i,j,step):#沿着横着走step步能得到的和 #上来就写边界条件: if i>chang-1 or j>kuan-1 or i<0 or j<0 or step==0: return -float('inf')#因为题目不要长度不够的数!!!!!!!!所以设置负无穷即可. if step==1: return ditu[i][j] return ditu[i][j]+qiuhe1(chang,kuan,i,j+1,step-1) def qiuhe2(chang,kuan,i,j,step):#沿着横着走step步能得到的和 #上来就写边界条件: if i>chang-1 or j>kuan-1 or i<0 or j<0 or step==0: return -float('inf') if step==1: return ditu[i][j] return ditu[i][j]+qiuhe2(chang,kuan,i+1,j,step-1) def qiuhe3(chang,kuan,i,j,step):#沿着横着走step步能得到的和 #上来就写边界条件: if i>chang-1 or j>kuan-1 or i<0 or j<0 or step==0: return -float('inf') if step==1: return ditu[i][j] return ditu[i][j]+qiuhe3(chang,kuan,i+1,j+1,step-1) def qiuhe4(chang,kuan,i,j,step):#沿着横着走step步能得到的和 #上来就写边界条件: if i>chang-1 or j>kuan-1 or i<0 or j<0 or step==0: return -float('inf') if step==1: return ditu[i][j] return ditu[i][j]+qiuhe4(chang,kuan,i+1,j-1,step-1) maxi=0 for i in range((chang)): for j in range((kuan)): maxi=max(maxi,qiuhe1(chang,kuan,i,j,d),qiuhe2(chang,kuan,i,j,d),qiuhe3(chang,kuan,i,j,d),qiuhe4(chang,kuan,i,j,d)) print(maxi) ''' ''' [编程题] 推箱子 时间限制:1秒 空间限制:32768K 大家一定玩过“推箱子”这个经典的游戏。具体规则就是在一个N*M的地图上,有1个玩家、1个箱子、1个目的地以及若干障碍,其余是空地。玩家可以往上下左右4个方向移动,但是不能移动出地图或者移动到障碍里去。如果往这个方向移动推到了箱子,箱子也会按这个方向移动一格,当然,箱子也不能被推出地图或推到障碍里。当箱子被推到目的地以后,游戏目标达成。现在告诉你游戏开始是初始的地图布局,请你求出玩家最少需要移动多少步才能够将游戏目标达成。 输入描述: 每个测试输入包含1个测试用例 第一行输入两个数字N,M表示地图的大小。其中0<N,M<=8。 接下来有N行,每行包含M个字符表示该行地图。其中 . 表示空地、X表示玩家、*表示箱子、#表示障碍、@表示目的地。 每个地图必定包含1个玩家、1个箱子、1个目的地。 输出描述: 输出一个数字表示玩家最少需要移动多少步才能将游戏目标达成。当无论如何达成不了的时候,输出-1。 输入例子1: 4 4 .... ..*@ .... .X.. 6 6 ...#.. ...... #*##.. ..##.# ..X... .@#... 输出例子1: 3 11 ''' ''' [编程题] 赛马 时间限制:1秒 空间限制:32768K 在一条无限长的跑道上,有N匹马在不同的位置上出发开始赛马。当开始赛马比赛后,所有的马开始以自己的速度一直匀速前进。每匹马的速度都不一样,且全部是同样的均匀随机分布。在比赛中当某匹马追上了前面的某匹马时,被追上的马就出局。 请问按以上的规则比赛无限长的时间后,赛道上剩余的马匹数量的数学期望是多少 输入描述: 每个测试输入包含1个测试用例 输入只有一行,一个正整数N 1 <= N <= 1000 输出描述: 输出一个浮点数,精确到小数点后四位数字,表示剩余马匹数量的数学期望 输入例子1: 1 2 输出例子1: 1.0000 1.5000 #看看数学上如何分析的,第i快的马货到最后概率是1/i+1 把马的速度设置为0到1之间的实数. 1.看每个马对于最后期望的贡献是多少? 2.最快的马显然是1 3.第二块的马,那么假设他的位置距离原点是x.初始位置是0到1的实数, 那么只有当最快的马在他前面他才能贡献期望1,否则贡献0.所以是(1-x)从0到1做积分.得到1/2 4........类似分析即可答案是调和级数. n = int(raw_input()) res = 0 for i in range(n): res += 1.0/(i+1) print r"%.4f" %res ''' ''' 倒水问题:这个题目的版本非常之多,有微软版的,腾讯版的,新浪版的等等,最常见的是给你一个容量为5升的桶和一个容量为3升的桶,水不限使用,要求精确得到4升水。 倒2次就完事了. [问题]有两个容桶,小桶的容量是4升,大桶的容量是9升,怎样才能从河中恰好打上6升水呢? 先大桶中弄好1升,然后给小桶,之后大桶从9开始给小桶即可. ''' ''' 为了解决倒水问题:先从基础抓起: 倒水问题 总时间限制: 1000ms 内存限制: 65536kB 描述 有三个分别容量分别为a升、b升和c升的杯子(a>b>c>0,且b与c互质)。 a杯装满水,b与c均为空。 三个筒相互倒水且不准把水倒往三个筒之外。 请用最少的倒水次数,倒出d升水(任一杯中正好水量为d 即可),并输出倒水的过程。 输入 只有一行:a、b、c、d 四个整数。 输出 第一行为倒水过程的总步骤 N ,其后N行为倒水的过程; 若无解,则输出“No find”。 样例输入 10 7 3 4 样例输出 3 10 0 0 3 7 0 3 4 3 明显的广搜,这里把vector、queue、stack都用了一遍 --------------------- 作者:zjc_617445 来源:CSDN 原文:https://blog.csdn.net/hsfz_zjc/article/details/75005668 版权声明:本文为博主原创文章,转载请附上博文链接! #include <cstdio> #include <queue> #include <stack> #include <vector> #include <algorithm> #include <iostream> #include <cstdlib> using namespace std; //结构体 struct node { int v[3]; int f; }; //全局变量 const int maxn=200+5; int a,b,c,d; bool tf[maxn][maxn]; int cap[3]; vector <node> vec; bool isok(int i) //判断是否倒水已经成功 { return vec[i].v[0]==d||vec[i].v[1]==d||vec[i].v[2]==d; } void out(int i) { int j; stack<int> sta; do { sta.push(i); if(vec[i].f!=i) i=vec[i].f; else break; }while(1) ; printf("%d ",sta.size() ); while(!sta.empty()) { j=sta.top() ;sta.pop() ; printf("%d %d %d ",vec[j].v[0],vec[j].v[1],vec[j].v[2]); } } void work(int a,int b,int c,int d) { //初始化 for(int i=0;i<maxn;i++) for(int j=0;j<maxn;j++) tf[i][j]=false; vec.clear() ; //准备 queue<int> que; int curr,ii; cap[0]=a; cap[1]=b; cap[2]=c; node s; if(a<d) { printf("No find");return; } s.v[0]=a;s.v[1]=0;s.v[2]=0;s.f =0; vec.push_back(s); if(isok(0)) { printf("1 %d 0 0",a);return; } tf[a][0]=true; que.push(0); //开始 while(!que.empty()) { curr=que.front(); que.pop() ; for(int i=0;i<3;i++) for(int j=0;j<3;j++) { //i->j // printf("** "); if(i==j||vec[curr].v[i]==0||vec[curr].v[j]==cap[j]) continue; // printf("44 "); ii=min(cap[j]-vec[curr].v[j],vec[curr].v[i]); s.f =curr; for(int o=0;o<3;o++) s.v [o]=vec[curr].v[o]; s.v[i]-=ii; s.v[j]+=ii; if(!tf[s.v[0]][s.v[1]]) { tf[s.v[0]][s.v[1]]=true; vec.push_back(s); if(isok(vec.size()-1)) { out(vec.size()-1); return; } que.push(vec.size() -1) ; } } } printf("No find"); } int main() { scanf("%d%d%d%d",&a,&b,&c,&d); work(a,b,c,d); return 0; } ''' ''' 题目要求 有两个容器,容积分别为A升和B升,有无限多的水,现在需要C升水。 我们还有一个足够大的水缸,足够容纳C升水。起初它是空的,我们只能往水缸里倒入水,而不能倒出。 可以进行的操作是: 把一个容器灌满; 把一个容器清空(容器里剩余的水全部倒掉,或者倒入水缸); 用一个容器的水倒入另外一个容器,直到倒出水的容器空或者倒入水的容器满。 问是否能够通过有限次操作,使得水缸最后恰好有C升水。 输入:三个整数A, B, C,其中 0 < A , B, C <= 1000000000 输出:0或1,表示能否达到要求。 函数头部: c语言:1表示可以,0表示不可以 int can(int a,int b,int c); c++语言: true表示可以,false表示不可以 bool can(int a,int b,int c); java语言:true表示可以,false表示不可以 public class Main { public static boolean can(int a,int b,int c); } 解题思路 自己分析: 比如按照大小顺序是a,b 那么可以拼出(ax-by) 这个恰好是最大公约数的公式,所以知道最大公约数可以被拼出来.从而公约数的倍数也是一样表达, 所以一样可以拼出来.那么需要证明的是不是最大公约数的倍数一定拼不出来! 证明:从倒水过程可以看出来能拼出来的数,算上倒掉的水.总体一定是ax+by.因为每一次加水都是加a或者加b,(因为杯子没有刻度).那么每一次倒掉的水也一定是a或者b的倍数.所以最后剩下的水也是ax+by. 所以显然是最大公约数的倍数.所以判断一个target是否能倒出来,只需要判断他是否是最大公钥数的倍数即可. 这是一个典型的倒水问题/量水问题,使用欧几里得算法就可解出来。 这里有一篇文章给出了简单的倒水问题的解法,可以解决笔试面试里面一些简单的填空题,可以看一看:http://blog.csdn.net/morewindows/article/details/7481851 基本思想是:不断用小桶装水倒入大桶,大桶满了立即清空,每次判断下二个桶中水的容量是否等于指定容量。也就是用小桶容量的倍数对大桶的容量进行取余,直到余数等于指定容量。 例如,用7升的桶和11升的桶得到2升水可以这样做: 7 % 11 = 7 14 % 11 = 3 21 % 11 = 10 28 % 11 = 6 35 % 11 = 2 成功得到2升水。 对于明确说明可以得到xx升水,需要我们给出如何倒出来的步骤,可以用这个方法,很快捷。但是这个方法不适合解这道题。 欧几里德算法又称辗转相除法,用于计算两个正整数a,b的最大公约数。 用gcd(a,b) 表示a, b的最大公约数,则有定理:gcd(a,b) = gcd(b,a mod b) (a>b 且a mod b 不为0) 具体的算法实现有循环和递归两种,我用的是循环的方法。 扩展欧几里得算法 定理:对于不完全为 0 的非负整数 a,b,gcd(a, b)表示 a, b 的最大公约数,必然存在整数对 x, y ,使得 gcd(a,b)=ax+by。 本题实际上是问是否存在整数x, y,使得ax+by=c成立。如果c可以被gcd(a,b)整除,则成立。 因此解题步骤如下: 1. 求出gcd(a,b) 2. 判断c是否能被gcd(a,b)整除,若能则返回true,否则返回false ''' ''' dfs:倒水 #这个题目看起来好像是一道模拟题,其实不然,这是一道dfs搜索题,只不过看起来好像无从下手,其实想想就好了,我们可以用一个vis数组来保存当前的状态如果之前某一次倒水出现过这种情况,我们就无需再次去遍历这种情况,只需要遍历其他情况就好了,还有一个重要的剪枝就是假如说我们已经找到某一种情况可以到达目标状态,那么深度再深的我们就无需再次去遍历,因为绝对不是最优解。 --------------------- 作者:caojiangxia 来源:CSDN 原文:https://blog.csdn.net/caojiangxia/article/details/46341005 版权声明:本文为博主原创文章,转载请附上博文链接! 抄点歌曲 [原][歌曲]感动的歌曲排序 故事: 起风了 买辣椒也用券 《起风了》情感历程 成长: 木马城市 毛不易 男孩长大为人 感悟: 在人间 王建房 爱情: 你还要我怎样 薛之谦 分手后的怀念 非常非常精彩的dp问题!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 理解了一点dp的本质就是函数递归,写好函数,然后递归调用.期间用动态规划. 注意flag的使用,和递归出来一般需要flag归位!!!!!!!!!! //当然这种题目也是,弄个几千或者几万直接就炸.毕竟np hard问题. #include<cstdio> #include<cstring> int a,b,c,t,vis[105][105];//题目:用a,b两个杯子如何倒出c这么多的水 //t表示深度,如果深度大于t就停止dp char s[205][15],s2[205][15],choice[][10]={"FILL(1)","FILL(2)","DROP(1)","DROP(2)","POUR(1,2)","POUR(2,1)"}; void dfs(int n,int m,int deep){ int dn,dm,i,j; if(deep>=t) return; //如果其中一个水杯已经满足有c单位的水就成功,所以这时候就让全局变量t设置为deep if(n==c||m==c){ t=deep; for(i=0;i<t;i++) strcpy(s2[i],s[i]);//把s的所有操作都给s2,作为保存 } //下面是6种操作分类讨论. strcpy(s[deep],choice[0]);//表示当前方法的第deep步使用的方法是choice[0] if(!vis[a][m]){//因为操作0是fill(1),所以得到的结果是第一个杯子满了是a,第二个杯子是m vis[a][m]=1;//表示进入 dfs(a,m,deep+1);//出来递归的时候,把这个flag再变回去,所以下面一行再设置为未访问. //非常牛逼的思路.当然比较朴素,但是我就是dp垃圾,感觉还是8皇后问题理解不够.自己想不到dp思路. vis[a][m]=0; } // strcpy(s[deep],choice[1]); if(!vis[n][b]){ vis[n][b]=1; dfs(n,b,deep+1); vis[n][b]=0;//递归出来一般需要flag归位!!!!!!!!!! } strcpy(s[deep],choice[2]); if(!vis[0][m]){ vis[0][m]=1; dfs(0,m,deep+1); vis[0][m]=0; } strcpy(s[deep],choice[3]); if(!vis[n][0]){ vis[n][0]=1; dfs(n,0,deep+1); vis[n][0]=0; } strcpy(s[deep],choice[4]); if(b-m>=n){ dn=0; dm=m+n; } else { dn=n-(b-m); dm=b; } if(!vis[dn][dm]){ vis[dn][dm]=1; dfs(dn,dm,deep+1); vis[dn][dm]=0; } strcpy(s[deep],choice[5]); if(a-n>=m){ dm=0; dn=m+n; }//不够倒满第一个杯子,所以第一个杯子m+n第二杯0 else { dm=m-(a-n); dn=a; }//够倒满所以第一个杯子a,第二个杯子m-a+n if(!vis[dn][dm]){ vis[dn][dm]=1; dfs(dn,dm,deep+1); vis[dn][dm]=0; } } int main(void){ int i; while(scanf("%d %d %d",&a,&b,&c)!=EOF){ t=1000000000; memset(vis,0,sizeof(vis)); dfs(0,0,0); if(t==1000000000) printf("impossible "); else{ printf("%d ",t); for(i=0;i<t;i++) printf("%s ",s2[i]); } } } ''' ''' [编程题] 倒置字符串 时间限制:1秒 空间限制:32768K 将一句话的单词进行倒置,标点不倒置。比如 I like beijing. 经过函数后变为:beijing. like I 输入描述: 每个测试输入包含1个测试用例: I like beijing. 输入用例长度不超过100 输出描述: 依次输出倒置之后的字符串,以空格分割 输入例子1: I like beijing. 输出例子1: beijing. like I a=input().split(' ') a=a[::-1] print(' '.join(a)) ''' ''' [编程题] 删除公共字符 时间限制:1秒 空间限制:32768K 输入两个字符串,从第一字符串中删除第二个字符串中所有的字符。例如,输入”They are students.”和”aeiou”,则删除之后的第一个字符串变成”Thy r stdnts.” 输入描述: 每个测试输入包含2个字符串 输出描述: 输出删除后的字符串 输入例子1: They are students. aeiou 输出例子1: Thy r stdnts. a1=input() a2=input() dex=[] for i in range(len(a1)): for j in range(len(a2)): if a1[i]==a2[j]: dex.append(i) out='' for i in range(len(a1)): if i not in dex: out+=a1[i] print(out) ''' ''' [编程题] 求和 时间限制:1秒 空间限制:32768K 输入两个整数 n 和 m,从数列1,2,3.......n 中随意取几个数,使其和等于 m ,要求将其中所有的可能组合列出来 //注意是取几个数,没说数量. 输入描述: 每个测试输入包含2个整数,n和m 输出描述: 按每个组合的字典序排列输出,每行输出一种组合 输入例子1: 5 5 输出例子1: 1 4 2 3 5 #又没写出来dp问题 [n,m]=[int(x) for x in input().split(' ')] l=[] #之前选的数 #总结这种需要返回分类后的结果的dp问题的思路: #1.先定义一个数组来存结果,因为这种递归问题都是逐步的解答,最后需要拼起来才是答案,所以需要数组2.之后定义函数f(n,m,k) k是开始index 3.对于函数先写边界值.也就是最后的判断输出点.即这个题目就是最后的m==0,就可以输出l了.4进行每一个分类的递归来跑遍.每一次都是先加入解l中跑完后再从l中剔除.跟倒水问题很像!!!!!!! def f(n,m,k): if m==0: print (' '.join(str(x)for x in l)) for i in range(k,n+1): if i>m: break l.append(i) f(n,m-i,i+1) l.pop() f(n,m,1) 自己写的: n,m=map(int,input().split()) l=[] out=[] def main(n,m,k):#k是index if m==0: out.append(l[:]) #注意因为数组的mutable属性.所以这里要复制 for i in range(k,(n)+1): if i>m: break l.append(i) main(n,m-i,k+1) l.pop() main(n,m,1) print(out) ''' ''' [编程题] 字符串中找出连续最长的数字串 时间限制:1秒 空间限制:32768K 读入一个字符串str,输出字符串str中的连续最长的数字串 输入描述: 个测试输入包含1个测试用例,一个字符串str,长度不超过255。 输出描述: 在一行内输出str中里连续最长的数字串。 输入例子1: abcd12345ed125ss123456789 输出例子1: 123456789 ''' ''' [编程题] n个数里最小的k个 时间限制:1秒 空间限制:32768K 找出n个数里最小的k个 输入描述: 每个测试输入包含空格分割的n+1个整数,最后一个整数为k值,n 不超过100。 输出描述: 输出n个整数里最小的k个数。升序输出 输入例子1: 3 9 6 8 -10 7 -11 19 30 12 23 5 输出例子1: -11 -10 3 6 7 ''' ''' [编程题] n个数里出现次数大于等于n/2的数 时间限制:1秒 空间限制:32768K 输入n个整数,输出出现次数大于等于数组长度一半的数。 输入描述: 每个测试输入包含 n个空格分割的n个整数,n不超过100,其中有一个整数出现次数大于等于n/2。 输出描述: 输出出现次数大于等于n/2的数。 输入例子1: 3 9 3 2 5 6 7 3 2 3 3 3 输出例子1: 3 都是水题不写了. ''' ''' [编程题] 幂运算 时间限制:1秒 空间限制:131072K 给定两个数R和n,输出R的n次方,其中0.0<R<99.999, 0<n<=25 输入描述: 多组测试用例,请参考例题的输入处理 输入每行一个浮点数 R 其中0.0 < R <99.999, 一个整数 n 其中0 < n <=25 输出描述: 输出R的n次方 输入例子1: 95.123 12 0.1 1 输出例子1: 548815620517731830194541.899025343415715973535967221869852721 0.1 ''' ''' [编程题] 几个岛 时间限制:1秒 空间限制:65536K 给定一个m行n列的二维地图, 初始化每个单元都是水. 操作addLand 把单元格(row,col)变成陆地. 岛屿定义为一系列相连的被水单元包围的陆地单元, 横向或纵向相邻的陆地称为相连(斜对角不算). 在一系列addLand的操作过程中, 给出每次addLand操作后岛屿的个数. 二维地图的每条边界外侧假定都是水. 输入描述: 多组测试数据,请参考例题处理 每组数据k+3行, k表示addLand操作次数 第一行:表示行数m 第二行:表示列数n 第三行:表示addLand操作次数k 第4~k+3行:row col 表示addLand的坐标。注意超过边界的坐标是无效的。 输出描述: 一行,k个整数, 表示每次addLand操作后岛屿的个数, 用空格隔开,结尾无空格 输入例子1: 3 3 4 0 0 0 1 1 2 2 1 输出例子1: 1 1 2 3 hang=int(input()) lie=int(input()) cishu=int(input()) if hang==0 or lie==0: print('') else: ditu=[[0]*lie for _ in range(hang)] output=[] for i in range((cishu)): a,b=map(int, input().split()) try:#因为有一个测试用例有bug,不在地图范围,所以用try ditu[a][b]=1 except: pass #下面判断当前ditu有几个岛屿,还是dp上下左右遍历. flag=[[0]*lie for _ in range(hang)] cnt=[0]#用这个cnt[0]来记录多少个独立的岛(因为数组是自动全局的所以这样写方便一些) def dp(hang,lie, a,b):#把a,b坐标的能连接岛屿的都设置为1 if a>hang-1 or b>lie-1 or a<0 or b<0 or ditu[a][b]==0 or flag[a][b]==1: return flag[a][b]=1 #判断是不是一个新岛 beixuan=[(a-1,b),(a,b-1),(a+1,b),(a,b+1)] beixuan2=[] for i in range(len(beixuan)): if beixuan[i][0]>hang-1 or beixuan[i][0]<0 or beixuan[i][1]>lie-1 or beixuan[i][1]<0: pass else: beixuan2.append(beixuan[i]) for i in range(len(beixuan2)): if ditu[beixuan2[i][0]][beixuan2[i][1]]==1 and flag[beixuan2[i][0]][beixuan2[i][1]]==1:#周围的点有走过的岛屿就是不是新的 shiNew=0 break else: shiNew=1 if shiNew==1: cnt[0]+=1 dp(hang,lie, a-1,b) dp(hang,lie, a,b-1) dp(hang,lie, a+1,b) dp(hang,lie, a,b+1) return for i in range((hang)): for j in range((lie)): dp(hang,lie,i,j) output.append(cnt[0]) for i in range(len(output)): output[i]=str(output[i]) print(' '.join(output)) ''' ''' 别人写 的上个题目.简练多了 m = int(input()) n = int(input()) k = int(input()) adl = [] for i in range(k): adl.append(map(int,raw_input().split()))#adl是添加过程 matrix是地图 def addland(i, j, m, n, matrix): #i, j = d[0], d[1] if i>=m or j >= n or i<0 or j<0 or matrix[i][j] == 0:return if matrix[i][j] == 1: matrix[i][j] = 0 addland(i+1, j, m, n, matrix) addland(i-1, j, m, n, matrix) addland(i, j+1, m, n, matrix) addland(i, j-1, m, n, matrix) return 1 result = [] for l in range(len(adl)): res = 0 matrix_g = [[0 for i in range(n)] for j in range(m)] for w in adl[:l+1]: if w[0]<m and w[1]<n: matrix_g[w[0]][w[1]] = 1 #matrix_g生成了当前步奏所生成的地图 for i in range(m): for j in range(n): if matrix_g[i][j] == 1: res += addland(i, j, m, n, matrix_g) result.append(str(res)) print ' '.join(result) 看看别人写的.我加上注释.果然牛逼.非常经典的题目,又学了很多技巧.!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! m = int(input()) n = int(input()) k = int(input()) adl = [] for i in range(k): adl.append([int(i)for i in input().split()])#adl是添加过程 matrix是地图 def addland(i, j, m, n, matrix): #i, j = d[0], d[1] if i>=m or j >= n or i<0 or j<0 :return 0 if matrix[i][j] == 1: matrix[i][j] = 0 #下面4步把周围的1变0,所以再访问到1就是一个孤立的岛屿!牛逼,这个太牛逼了. #道理就是比如矩阵[[1, 1], [0, 0]],访问第一个一的时候,就进入递归调用访问addland(0, 1, m, n, matrix),但是调用后不管他返回多少,我都没获得,因为我只回收addland(0, 0, m, n, matrix),但是这部调用把[0,1]坐标的值给修改成0了,所以下次访问就访问不到[0,1]坐标了.从而这个4步递归等效于把岛屿这个点临街的岛屿都给抹杀了.递归下去就是把跟[0,0]相连的岛屿都抹杀,从而下次加的就是新的独立岛屿!虽然短但是牛逼的代码! addland(i+1, j, m, n, matrix) addland(i-1, j, m, n, matrix) addland(i, j+1, m, n, matrix) addland(i, j-1, m, n, matrix) return 1 result = [] for l in range(len(adl)): res = 0 matrix_g = [[0 for i in range(n)] for j in range(m)] for w in adl[:l+1]: if w[0]<m and w[1]<n: matrix_g[w[0]][w[1]] = 1 #matrix_g生成了当前步奏所生成的地图 print(matrix_g) for i in range(m): for j in range(n): if matrix_g[i][j] == 1: res += addland(i, j, m, n, matrix_g) result.append(str(res)) print (' '.join(result)) ''' ''' 首页 题库 学习 求职 讨论区 发现 搜索 APP 消息 44/44 00:03:45 [编程题] CIDR去重 时间限制:1秒 空间限制:65536K #无类别域间路由(CIDR)是一个用于对IPV4地址进行分类表述的方法。CIDR 路由描述的IP地址组的子网mask长度是可变长度, 例如10.0.0.0/22 表示前22位和10.0.0.0相同的网络地址都被覆盖, 22包含了10.0这前两个字段(0-7位,8-15位)和第三个字段的前6位(16-21,即0b000000**), 涵盖了 10.0.0.*, 10.0.1.*, 10.0.2.*, 10.0.3.* 四组ip地址. 在此前提下请实现IP网络中的一个常用的去重操作: 给定一系列 CIDR 路由地址, 其中没有完全等价的路由, 去掉被重复表示的 CIDR 路由, 即去掉已经被其他CIDR路由表示覆盖的路由地址. 例如 10.0.1.1/32 已经被 10.0.0.0/22覆盖了, 如果路由列表中已经有了后者, 就可以去掉前者. 输入描述: k+1行, k表示输入的CIDR路由个数 第1行:表示路由个数k 第2~k+1行: 表示一个CIDR路由, 形如 x.x.x.x/x 输出描述: n+1行, n表示去重后剩下的CIDR路由个数 第1行:n 第2~n+1行: 表示一个去重后的CIDR路由, 输出按照输入顺序 输入例子1: 13 192.168.0.0/16 172.24.96.17/32 172.50.137.225/32 202.139.219.192/32 172.24.68.0/24 192.183.125.71/32 201.45.111.138/32 192.168.59.211/32 192.168.26.13/32 172.24.0.0/17 172.24.5.1/32 172.24.68.37/32 172.24.168.32/32 输出例子1: 7 192.168.0.0/16 172.50.137.225/32 202.139.219.192/32 192.183.125.71/32 201.45.111.138/32 172.24.0.0/17 172.24.168.32/32 ''' ''' [编程题] 最短字符编码 时间限制:1秒 空间限制:65536K 给定一个非空字符串, 按照如下方式编码, 使得编码后长度最小, 返回编码后的长度: 编码规则为: k[encoding_string], 表示重复k次encoding_strng, 例如'abcdefabcdefabc'可表示为'2[abcdef]abc', 但是'aaa'仅能编码成'aaa', 因为len('3[a]')>len('aaa'). 补充: 1. k为正整数, []内的encoding_string不得含有空格不得为空; 2. []内的encoding_string 本身可以为编码过的字符串, 例如'abcdabcdeabcdabcde' 可以编码为 '2[abcdabcde]'(编码后长度从18减少到12), []内的'abcdabcde'又可以编码为 '2[abcd]e', 最终编码为 '2[2[abcd]e]', 编码后长度为11, 应返回11; 这个编码路径也能是: 'abcdabcdeabcdabcde' -> '2[abcd]e2[abcd]e' -> '2[2[abcd]e]'; 2. 输入字符串为全小写英文字母, 长度<=160; 3. 如果编码后长度没有更小, 则保留原有字符串; 输入描述: 一行数据, 表示输入字符串 输出描述: 输出一个字符串表示编码后长度 输入例子1: aaa 输出例子1: 3 例子说明1: aaa,长度3 输入例子2: aaaaa 输出例子2: 4 例子说明2: 5[a],长度4 输入例子3: aabcaabcd 输出例子3: 8 例子说明3: 2[aabc]d,长度8 a=input() memo={} def main(a):#返回a最小能压缩到的结果 if a in memo: return memo[a] new=a mini=len(a) for j in range(len(a)-4):#切分点是j for i in range(1,len(a)//2+1):#长度是i start=0 while a[j:i+j]==a[j+(start+1)*i:j+(start+2)*i]: start+=1 tmp=main(a[:j])+str(start+1)+'['+main(a[j:i+j])+']'+main(a[j+(start+1)*i:]) if len(tmp)<mini: new=tmp mini=len(tmp) memo[a]=new return memo[a] #还需要继续讨论不是从头开始折叠的情况. #print((main(a)) ) print(len(main(a)) )#这么写超时 #通过对下面别人代码的分析,他的memo里面是记录可以压缩才进去,而我的是都放进去,所以他的更节省空间和时间. ''' ''' def check(a, i, j): if i + (j - i) * 2 > len(a): return False, a p, q = i, j adjust = 0 while q <= len(a): if a[p:q] == a[q:q + q - p]: p, q = q, q + q - p adjust = adjust + 1 else: break if adjust > 0: res = a[:i] + str(adjust+1) + '[' + a[i:j] + ']' + a[q:] if len(res) <= len(a): return True, res return False, a def solve(a): res = [len(a)] table = dict() def change(a): if len(a) > 4: for i in range(len(a) - 1): for j in range( i+1,len(a) - 1): c, tmp = check(a, i, j) if c: if len(tmp) < res[0]: res[0] = len(tmp) if tmp not in table: table[tmp] = True change(tmp)#原来是在这里来进行递归操作!!!!!!!!!! change(a) return res[0] if __name__ == "__main__": a = input().strip() print(solve(a)) ''' ''' [编程题] xor 时间限制:1秒 空间限制:65536K 给出n个数字 a_1,...,a_n,问最多有多少不重叠的非空区间,使得每个区间内数字的xor都等于0。 输入描述: 第一行一个整数n; 第二行n个整数 a_1,...,a_n; 对于30%的数据,n<=20; 对于100%的数据,n<=100000, a_i<=100000; 输出描述: 一个整数表示最多的区间个数; 输入例子1: 4 3 0 2 2 输出例子1: 2 题意不懂.直接看答案 n=int(input()) #n=4 A=[] l=raw_input() A=[int(x) for x in l.split()] #3 0 2 2 m={} m[0]=1 r=0 ans=0 for a in A: ans^=a if ans in m: r+=1 m.clear() m[ans]=1 print r ''' ''' [编程题] CIDR去重 时间限制:1秒 空间限制:65536K #无类别域间路由(CIDR)是一个用于对IPV4地址进行分类表述的方法。CIDR 路由描述的IP地址组的子网mask长度是可变长度, 例如10.0.0.0/22 表示前22位和10.0.0.0相同的网络地址都被覆盖, 22包含了10.0这前两个字段(0-7位,8-15位)和第三个字段的前6位(16-21,即0b000000**), 涵盖了 10.0.0.*, 10.0.1.*, 10.0.2.*, 10.0.3.* 四组ip地址. 因为前面22为是网络地址,所以已经确定了.所以是0*....4*这些可以变化. 在此前提下请实现IP网络中的一个常用的去重操作: 给定一系列 CIDR 路由地址, 其中没有完全等价的路由, 去掉被重复表示的 CIDR 路由, 即去掉已经被其他CIDR路由表示覆盖的路由地址. 例如 10.0.1.1/32 已经被 10.0.0.0/22覆盖了, 为什么覆盖了?需要转化成2进制来看 如果路由列表中已经有了后者, 就可以去掉前者. 输入描述: k+1行, k表示输入的CIDR路由个数 第1行:表示路由个数k 第2~k+1行: 表示一个CIDR路由, 形如 x.x.x.x/x 输出描述: n+1行, n表示去重后剩下的CIDR路由个数 第1行:n 第2~n+1行: 表示一个去重后的CIDR路由, 输出按照输入顺序 输入例子1: 13 192.168.0.0/16 172.24.96.17/32 172.50.137.225/32 202.139.219.192/32 172.24.68.0/24 192.183.125.71/32 201.45.111.138/32 192.168.59.211/32 192.168.26.13/32 172.24.0.0/17 172.24.5.1/32 172.24.68.37/32 172.24.168.32/32 输出例子1: 7 192.168.0.0/16 172.50.137.225/32 202.139.219.192/32 192.183.125.71/32 201.45.111.138/32 172.24.0.0/17 172.24.168.32/32 根据分析,用2进制转化后按照长度排序后去重即可.最后按照原始顺序输出即可 num=int(input()) save=[] save3=[] for i in range((num)): tmp=input() a=tmp.split('/')[0] b=int(tmp.split('/')[1]) arr=a.split('.') save.append((arr,b)) save3.append(tmp) save=sorted(save,key=lambda x:x[1]) save2=[] for i in save: arr=i[0] b=str(i[1]) save2.append('.'.join(arr)+'/'+b) #按照长度排序,因为为了避免先判断长的. #转化到2进制 out_dex=[] out=[] for i in range(len(save)): arr=save[i][0] b=save[i][1] for j in range(len(arr)): arr[j]=bin(int(arr[j]))[2:] arr[j]=(8-len(arr[j]))*'0'+arr[j] b=int(b) now=''.join(arr)[:b] for j in out: if now[:len(j)]==j: break else: out.append(now) out_dex.append(i) output=[] for i in out_dex: output.append(save2[i]) print(len(output)) for i in save3: #为了变回之前的顺序. if i in output: print(i) ''' ''' 滴滴出行2017秋招笔试真题-编程题汇总 [编程题] 连续最大和 时间限制:1秒 空间限制:32768K 一个数组有 N 个元素,求连续子数组的最大和。 例如:[-1,2,1],和最大的连续子数组为[2,1],其和为 3 输入描述: 输入为两行。 第一行一个整数n(1 <= n <= 100000),表示一共有n个元素 第二行为n个数,即每个元素,每个整数都在32位int范围内。以空格分隔。 输出描述: 所有连续子数组中和最大的值。 输入例子1: 3 -1 2 1 输出例子1: 3 继续联系基本功. a=int(input()) b=[int(i)for i in input().split()] out=b[0] maxi=b[0] for i in range(1,len(b)): if out<0: out=0 out+=b[i] maxi=max(out,maxi) print(maxi) ''' ''' [编程题] 餐馆 时间限制:1秒 空间限制:65536K 某餐馆有n张桌子,每张桌子有一个参数:a 可容纳的最大人数; 有m批客人,每批客人有两个参数:b人数,c预计消费金额。 在不允许拼桌的情况下,请实现一个算法选择其中一部分客人,使得总预计消费金额最大 输入描述: 输入包括m+2行。 第一行两个整数n(1 <= n <= 50000),m(1 <= m <= 50000) 第二行为n个参数a,即每个桌子可容纳的最大人数,以空格分隔,范围均在32位int范围内。 接下来m行,每行两个参数b,c。分别表示第i批客人的人数和预计消费金额,以空格分隔,范围均在32位int范围内。 输出描述: 输出一个整数,表示最大的总预计消费金额 输入例子1: 3 5 2 4 2 1 3 3 5 3 7 5 9 1 10 输出例子1: 20 贪心法:选人数少,消费高的给最小的桌子. n,m=map(int,input().split()) arr=[int(i)for i in input().split()] keren=[] for i in range(m): keren.append([int(i)for i in input().split()]) keren=sorted(keren,key=lambda x:(x[0],-x[1]))#第一个升序如果相同按照第二个降序 out=0 arr.sort() # print(arr) # print(keren) dex=[] for i in range(len(arr)): tmp_dex=None tmp=0 for j in range(len(keren)): if keren[j][0]<=arr[i] and j not in dex and keren[j][1]>tmp: tmp=keren[j][1] tmp_dex=j # print(99999999999) # print(tmp_dex) dex.append(tmp_dex) newdex=[] for i in range(len(dex)): if dex[i]!=None: newdex.append(dex[i]) dex=newdex # print(newdex) he=0 # print(keren) # print(he) for i in ((newdex)): he+=keren[i][1] print(he) ''' ''' 上面问题完全ac代码.用2分加速查找! import sys #用2分来找index def getindex(data,k):#返回data这个数组中大于=k的最小坐标 i = 0 j = len(data)-1 result=1<<30 while(i<=j): mid = (i+j)//2 if data[mid]>=k: result = min(mid,result) j = mid-1 else: i = mid+1 return result n,m = map(int,input().split()) data = map(int,input().split())#桌子大小 mat = []#客人数据 for i in range(m): mat.append([int(i)for i in input().split()]) data=list(data) data.sort() mat=list(mat) newmat=sorted(mat,key=lambda x:(-x[1],x[0])) #排序按照,消费大的顾客优先.反正:如果消费最大的顾客可以满足,但是你不选他,那么最大的桌子的顾客肯定没有这个消费最大的顾客消费的多,所以如果不选这个消费最大的可以满足他的顾客,那么你得到的解就不是最优的.#所以排序要按照消费排序,当消费一样的时候优先满足要求低的,因为他可以最大限度的节省桌子这个资源. #print(newmat) #print newmat result = 0 #print(data) while(len(data)>0 and len(newmat)>0): num = newmat.pop(0) nums = num[0] #每一次为消费最大的顾客分配一个桌子 k = getindex(data,nums) if k != 1<<30: result+=num[1] data.pop(k) print (result) ''' ''' 按照相同思路自己写一份: import sys #用2分来找index def getindex(data,k):#返回data这个数组中大于=k的最小坐标,如果找不到就返回None first=0 end=len(data)-1 res=1<<30 #大神都用res作为结果 while end-first>1: mid=(first+end)//2 if data[mid]>=k: end=mid res=min(res,end) else: first=mid if data[first]>=k: return first if data[end]>=k: return end return res n,m = map(int,input().split()) data = map(int,input().split())#桌子大小 mat = []#客人数据 for i in range(m): mat.append([int(i)for i in input().split()]) data=list(data) data.sort() mat=list(mat) newmat=sorted(mat,key=lambda x:(-x[1],x[0])) #排序按照,消费大的顾客优先.反正:如果消费最大的顾客可以满足,但是你不选他,那么最大的桌子的顾客肯定没有这个消费最大的顾客消费的多,所以如果不选这个消费最大的可以满足他的顾客,那么你得到的解就不是最优的.#所以排序要按照消费排序,当消费一样的时候优先满足要求低的,因为他可以最大限度的节省桌子这个资源. #print(newmat) #print (newmat) result = 0 #print(data) while(len(data)>0 and len(newmat)>0): num = newmat.pop(0) nums = num[0] #每一次为消费最大的顾客分配一个桌子 k = getindex(data,nums) # print(k) if k != 1<<30: result+=num[1] data.pop(k) print (result) ''' ''' [编程题] 地下迷宫 时间限制:1秒 空间限制:32768K ##小青蛙有一天不小心落入了一个地下迷宫,小青蛙希望用自己仅剩的体力值P跳出这个地下迷宫。为了让问题简单,假设这是一个n*m的格子迷宫,迷宫每个位置为0或者1,0代表这个位置有障碍物,小青蛙达到不了这个位置;1代表小青蛙可以达到的位置。小青蛙初始在(0,0)位置,地下迷宫的出口在(0,m-1)(保证这两个位置都是1,并且保证一定有起点到终点可达的路径),小青蛙在迷宫中水平移动一个单位距离需要消耗1点体力值,向上爬一个单位距离需要消耗3个单位的体力值,向下移动不消耗体力值,当小青蛙的体力值等于0的时候还没有到达出口,小青蛙将无法逃离迷宫。现在需要你帮助小青蛙计算出能否用仅剩的体力值跳出迷宫(即达到(0,m-1)位置)。 输入描述: 输入包括n+1行: 第一行为三个整数n,m(3 <= m,n <= 10),P(1 <= P <= 100) 接下来的n行: 每行m个0或者1,以空格分隔 输出描述: 如果能逃离迷宫,则输出一行体力消耗最小的路径,输出格式见样例所示;如果不能逃离迷宫,则输出"Can not escape!"。 测试数据保证答案唯一 输入例子1: 4 4 10 1 0 0 1 1 1 0 1 0 1 1 1 0 0 1 1 输出例子1: [0,0],[1,0],[1,1],[2,1],[2,2],[2,3],[1,3],[0,3] 非常精彩的题目:是滴滴2017年的笔试题目.相当考验2维map的dp算法. n,m,p=map(int,input().split()) ditu=[] for i in range((n)): ditu.append([int(i)for i in input().split()]) flag=[[0]*m for _ in range(n)] lujing=[] mini=float('inf') save=[1] dic={} #通过立flag来避免循环递归,递归出去再flag回来 def search(n,m,i,j,p):#返回这个点到终点的最好路线,其实就是按照倒水问题套dp算法 #地图n*m 当前位置i,j, 返回当前位置到最终点最好路线需要多少个p值 #p表示从入口到现在消耗的p,因为这个题目需要设置p值,所以比倒水问题难一点应该. lujing.append([i,j]) # print(lujing) if i==0 and j == m-1: #现在拼出最后路径做保存即可 global mini#因为需要修改mini#python对于变量是默认都能访问,但是只有global的才能修改.数组默认global if p<mini: #save=lujing#保存列表不能直接写等,只能用元素赋值来传出去 #下面问题就是怎么把这个传出去,因为数组mutable特性,所以这里别忘了复制列表 dic[1]=lujing[:] mini=p return if i>n-1 or j>m-1 or i<0 or j<0 or ditu[i][j]==0 or flag[i][j]==1: return flag[i][j]=1 #递归 search(n,m,i-1,j,p+3) lujing.pop() search(n,m,i+1,j,p) lujing.pop() search(n,m,i,j-1,p+1) lujing.pop() search(n,m,i,j+1,p+1) lujing.pop() flag[i][j]=0 search(n,m,0,0,0) out=dic[1] out=str(out) out=out.replace(' ','') if mini<=p: print(out[1:-1]) else: print("Can not escape!") '''
2018-10-23,21点43 笔试题先做到这些,学习项目,等学无聊了再回来做算法题

#下面这一段用一个txt来保存input的信息来模拟input.最后提交代码时候删除这一段即可. a9999=open('1.txt','r') def input(): return a9999.readline().rstrip(' ') #输入数据的一些模板 # n,a=map(int,input().split()) # arr=[int(i)for i in input().split()] # 格式化输出 # print('%.2f'%(maxi/2)) ''' # 最大公约数用 import fractions fractions.gcd(a,b) #多个分隔符: import re b=re.split('[+*-]',a) ''' ''' [编程题] 魔力手环 时间限制:1秒 空间限制:32768K 小易拥有一个拥有魔力的手环上面有n个数字(构成一个环),当这个魔力手环每次使用魔力的时候就会发生一种奇特的变化:每个数字会变成自己跟后面一个数字的和(最后一个数字的后面一个数字是第一个),一旦某个位置的数字大于等于100就马上对100取模(比如某个位置变为103,就会自动变为3).现在给出这个魔力手环的构成,请你计算出使用k次魔力之后魔力手环的状态。 输入描述: 输入数据包括两行: 第一行为两个整数n(2 ≤ n ≤ 50)和k(1 ≤ k ≤ 2000000000),以空格分隔 第二行为魔力手环初始的n个数,以空格分隔。范围都在0至99. 输出描述: 输出魔力手环使用k次之后的状态,以空格分隔,行末无空格。 输入例子1: 3 2 1 2 3 输出例子1: 8 9 7 Python3(3.5.2)重置自测 1 先找规律: 比如3个数: a,b,c turn1: a+b b+c c+a turn2: a+2b+c b+2c+a c+2a+b turn3: 2a+3b+3c 2b+3c+3a 2c+3a+3b turn4: 5a+5b+6c 5b+6a+5c 5c+5a+6b #只能这样了,应该是因为python3的速度太慢了 #看了网友的答案,原来这种高效率递归问题用矩阵幂来解决. #(a1,....an)=(a1,....an)(x1,...xn) 就是对角线和次对焦都是1的矩阵. #矩阵高次幂用算2次.....2^n次拼起来即可. n,k=map(int,input().split())#题目k取2e11 arr=[int(i)for i in input().split()] def multi(a,b):#a,b是同介方阵 c=[[0]*len(a)for _ in range(len(a))] #注意二维矩阵的写法,外层不要写乘因为list的mute属性问题!!!!!!! for i in range(len(a)): for j in range(len(a)): for k in range(len(a)): c[i][j]+=a[i][k]*b[k][j] c[i][j]%=100 return (c) matrix=[[0]*len(arr)for _ in range (len(arr))] #变换矩阵 matrix[0][0]=1 matrix[0][len(matrix)-1]=1 for i in range(1,len(matrix)): matrix[i][i]=1 matrix[i][i-1]=1 def multiK(mat,k):#求矩阵mat的k次幂,这个算法需要熟悉理解 danwei=[[0]*len(mat)for _ in range(len(mat))] for i in range(len(danwei)): danwei[i][i]=1 out=danwei #这里用单位矩阵来出事话 while k : if k&1==1:#当k的2进制最后一位是1,那么输出就乘一下mat,然后mat自平方,k>>1 out = multi(out,mat) mat = multi(mat,mat) k = k>>1 else: mat = multi(mat,mat) k = k>>1 return out #下面把arr跟multiK(matrix,k)乘一下,注意行列 out=[0]*len(matrix) for i in range(len(matrix)): for j in range(len(matrix)): out[i]+=arr[j]*multiK(matrix,k)[j][i] out[i]%=100 for i in range(len(out)): out[i]=str(out[i]) print(' '.join(out)) 提交运行 提前交卷下一题 收藏本题 标记一下 提交结果有问题? 收起答题卡 ''' ''' # [编程题] 工作安排 # 时间限制:1秒 # 空间限制:32768K # 现在有n位工程师和6项工作(编号为0至5),现在给出每个人能够胜任的工作序号表(用一个字符串表示,比如:045,表示某位工程师能够胜任0号,4号,5号工作)。现在需要进行工作安排,每位工程师只能被安排到自己能够胜任的工作当中去,两位工程师不能安排到同一项工作当中去。如果两种工作安排中有一个人被安排在的工作序号不一样就被视为不同的工作安排,现在需要计算出有多少种不同工作安排计划。 输入描述: 输入数据有n+1行: 第一行为工程师人数n(1 ≤ n ≤ 6) 接下来的n行,每行一个字符串表示第i(1 ≤ i ≤ n)个人能够胜任的工作(字符串不一定等长的) 输出描述: 输出一个整数,表示有多少种不同的工作安排方案 输入例子1: 6 012345 012345 012345 012345 012345 012345 输出例子1: 720 n=int(input()) arr=[input() for _ in range(n)] left=range(6) def main(dex,left):#返回剩余工作left,给dex拍工作 这个数量. cnt=0 if dex==n-1: tmp=[str(i) for i in left] a=0 for i in tmp: if i in arr[dex]: a+=1 return a for i in range(len(left)): if str(left[i]) in arr[dex]: now=left[:] now=list(now) now.pop(i) cnt+=main(dex+1,now) return cnt if left==[]: print(0) else: print(main(0,left)) ''' ''' [编程题] 集合 时间限制:1秒 空间限制:32768K 小易最近在数学课上学习到了集合的概念,集合有三个特征:1.确定性 2.互异性 3.无序性. 小易的老师给了小易这样一个集合: S = { p/q | w ≤ p ≤ x, y ≤ q ≤ z } 需要根据给定的w,x,y,z,求出集合中一共有多少个元素。小易才学习了集合还解决不了这个复杂的问题,需要你来帮助他。 输入描述: 输入包括一行: 一共4个整数分别是w(1 ≤ w ≤ x),x(1 ≤ x ≤ 100),y(1 ≤ y ≤ z),z(1 ≤ z ≤ 100).以空格分隔 输出描述: 输出集合中元素的个数 输入例子1: 1 10 1 1 输出例子1: 10 w,x,y,z=map(int,input().split()) a=set([]) for i in range(w,x+1): for j in range(y,z+1): a.add(i/j) print(len(a)) ''' ''' [编程题] 奇怪的表达式求值 时间限制:1秒 空间限制:32768K 常规的表达式求值,我们都会根据计算的优先级来计算。比如*/的优先级就高于+-。但是小易所生活的世界的表达式规则很简单,从左往右依次计算即可,而且小易所在的世界没有除法,意味着表达式中没有/,只有(+, - 和 *)。现在给出一个表达式,需要你帮忙计算出小易所在的世界这个表达式的值为多少 输入描述: 输入为一行字符串,即一个表达式。其中运算符只有-,+,*。参与计算的数字只有0~9. 保证表达式都是合法的,排列规则如样例所示。 输出描述: 输出一个数,即表达式的值 输入例子1: 3+5*7 输出例子1: 56 a=input() import re b=re.split('[+*-]',a) fuhao=[] for i in range(len(a)): if a[i] in '+-*': fuhao.append(a[i]) while len(b)!=1: tmp=b[0]+fuhao[0]+b[1] fuhao.pop(0) b=[str(eval(tmp))]+b[2:] print(b[0]) ''' ''' 编程题] 涂棋盘 时间限制:1秒 空间限制:32768K 小易有一块n*n的棋盘,棋盘的每一个格子都为黑色或者白色,小易现在要用他喜欢的红色去涂画棋盘。小易会找出棋盘中某一列中拥有相同颜色的最大的区域去涂画,帮助小易算算他会涂画多少个棋格。 输入描述: 输入数据包括n+1行: 第一行为一个整数n(1 ≤ n ≤ 50),即棋盘的大小 接下来的n行每行一个字符串表示第i行棋盘的颜色,'W'表示白色,'B'表示黑色 输出描述: 输出小易会涂画的区域大小 输入例子1: 3 BWW BBB BWB 输出例子1: 3 a=int(input()) b=[] for i in range((a)): tmp=input() base=[] for i in tmp: base.append(i) b.append(base) #不用numpy实现矩阵转至 tmp=[] for i in range(len(b)): save=[] for j in range(len(b)): save.append(b[j][i]) tmp.append(save) memo=[] for i in tmp: maxi=0 cnt=1 for j in range(1,len(i)): if i[j]==i[j-1]: cnt+=1 maxi=max(maxi,cnt) else: maxi=max(maxi,cnt) cnt=1 memo.append(maxi) print(max(memo)) ''' ''' [编程题] 小易记单词 时间限制:1秒 空间限制:32768K 小易参与了一个记单词的小游戏。游戏开始系统提供了m个不同的单词,小易记忆一段时间之后需要在纸上写出他记住的单词。小易一共写出了n个他能记住的单词,如果小易写出的单词是在系统提供的,将获得这个单词长度的平方的分数。注意小易写出的单词可能重复,但是对于每个正确的单词只能计分一次。 输入描述: 输入数据包括三行: 第一行为两个整数n(1 ≤ n ≤ 50)和m(1 ≤ m ≤ 50)。以空格分隔 第二行为n个字符串,表示小易能记住的单词,以空格分隔,每个单词的长度小于等于50。 第三行为m个字符串,系统提供的单词,以空格分隔,每个单词的长度小于等于50。 输出描述: 输出一个整数表示小易能获得的分数 输入例子1: 3 4 apple orange strawberry strawberry orange grapefruit watermelon 输出例子1: 136 n,m=map(int,input().split()) jiyi=input().split()[:n] #这个题目有bug这里面他给的多了,所以需要些:n来切片即可. xitong=input().split()[:m] jiyi=set(jiyi) xitong=set(xitong) cnt=0 for i in jiyi: if i in xitong: cnt+=len(i)**2 print(cnt) ''' ''' [编程题] 堆砖块 时间限制:1秒 空间限制:32768K 小易有n块砖块,每一块砖块有一个高度。小易希望利用这些砖块堆砌两座相同高度的塔。为了让问题简单,砖块堆砌就是简单的高度相加,某一块砖只能使用在一座塔中一次。小易现在让能够堆砌出来的两座塔的高度尽量高,小易能否完成呢。 输入描述: 输入包括两行: 第一行为整数n(1 ≤ n ≤ 50),即一共有n块砖块 第二行为n个整数,表示每一块砖块的高度height[i] (1 ≤ height[i] ≤ 500000) 输出描述: 如果小易能堆砌出两座高度相同的塔,输出最高能拼凑的高度,如果不能则输出-1. 保证答案不大于500000。 输入例子1: 3 2 3 5 输出例子1: 5 这个题目动态规划还可以.是相当可以了,非常难.因为他的递归不是按照index,而是按照高度差 ''' ''' 别人的java答案:非常牛逼: 链接:https://www.nowcoder.com/questionTerminal/040924ba0e64423b8a3fe2f75a56934a 来源:牛客网 /** 思路来自于csdn上,大概看了一次,这次是完全凭记忆写出来的,主要的就是利用动态规划的思想, dp[i][j]表示在使用前i块砖,高度差为j时低塔的高度,考虑四种情况: 1. 新砖块放在低塔上,:低塔依然是低塔,即 dp[i][j] = dp[i-1][j+high] + high; 2. 新砖块放在低塔上,低塔变成了高塔,即: dp[i][j] = dp[i-1][high-j] + high-j; 3. 新砖块放在高塔上,高塔只可能是高塔,即: dp[i][j] = dp[i-1][j-high]; 4. 放弃新砖块,不放在任何一个塔上,即: dp[i][j] = dp[i-1][j]; 最终dp[i][j]取以上四种情况的最大值即可; 如果直接定义n*sum维的数组,内存会不够,所以优化了一下内存,应该有更好的方法,再学习了 */ import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); while (sc.hasNext()) { int n = sc.nextInt(); int[] h = new int[n]; int sum = 0; for (int i = 0; i < n; i++) { h[i] = sc.nextInt(); sum += h[i]; } //sum表示所有砖块的总和 int[][] dp = new int[2][sum+1]; //dp[i][j] 定义2 是因为利用滚动数组,表示前i个砖块中,堆成的塔,高度差为j时,低塔的最高高度 所以最后需要返回i是n,j为0的时候的解即可. for (int i = 0; i < 2; i++) { for (int j = 0; j < sum + 1; j++) { dp[i][j] = Integer.MIN_VALUE; //初始化为负无穷,表示没有这种高度的堆法 } } dp[0][0] = 0; //如果没有放砖的时候,低塔为0,高度差为0 for (int i = 0; i < n; i++) { int high = h[i]; //比如放第二个砖块之前,high就是第一个砖块????????这个地方不理解 //核心就是下面4行代码! for (int j = 0; j <= sum; j++) { //非常精彩的4个推理!!!!!!!!!!!!!!!!!!!!!!!!!!!!! if(j > high) { //如果将砖块放在高塔上,则低塔高度不变,高度差增加 //之前的差是j-high,现在的高是j,high表示当前需要插入的砖的高度 dp[1][j] = Math.max(dp[1][j], dp[0][j - high]); } else {//如果当前插入砖的高度>=j //如果将砖块放在低塔上,低塔变高塔,高塔高度变低塔高度,高度差改变 dp[1][j] = Math.max(dp[1][j], dp[0][high - j] + (high - j)); } //如果将新砖块放在低塔上,并且依然是低塔,则低塔高度增加 if(j + high <= sum) dp[1][j] = Math.max(dp[1][j], dp[0][j + high] + high); //放弃该砖块,不放在任何一个塔上 dp[1][j] = Math.max(dp[1][j], dp[0][j]); } System.arraycopy(dp[1], 0, dp[0], 0, sum + 1);//交换数组的数据,所以不管数据n是多少,最后的数据总是在dp[0]里面. for (int j = 0; j <= sum; j++) { dp[1][0] = Integer.MIN_VALUE; } } if(dp[0][0] > 0) System.out.println(dp[0][0]); else System.out.println(-1); } } } ''' ''' [编程题] 分饼干 时间限制:1秒 空间限制:32768K 易老师购买了一盒饼干,盒子中一共有k块饼干,但是数字k有些数位变得模糊了,看不清楚数字具体是多少了。易老师需要你帮忙把这k块饼干平分给n个小朋友,易老师保证这盒饼干能平分给n个小朋友。现在你需要计算出k有多少种可能的数值 输入描述: 输入包括两行: 第一行为盒子上的数值k,模糊的数位用X表示,长度小于18(可能有多个模糊的数位) 第二行为小朋友的人数n 输出描述: 输出k可能的数值种数,保证至少为1 输入例子1: 9999999999999X 3 输出例子1: 4 a=input() b=int(input()) #小朋友数量是b n=b #dfs显然超时,尝试用动态规划才是正确的方法.dp[i][j]表示使用字符前i个,除小朋友个数n后余j的个数. dp=[[0]*b for _ in range(len(a)+1)] dp[0][0]=1#表示什么字符都不用,所以i取len(a)就表示用了全部字符 for i in range(1,len(a)+1): for j in range((b)): if a[i-1]=='X': for _ in range((10)): dp[i][(10*j+_)%n]+=dp[i-1][j] else: dp[i][(10*j+int(a[i-1]))%n]+=dp[i-1][j] print(dp[-1][0]) ''' ''' [编程题] 年终奖 时间限制:3秒 空间限制:32768K 小东所在公司要发年终奖,而小东恰好获得了最高福利,他要在公司年会上参与一个抽奖游戏,游戏在一个6*6的棋盘上进行,上面放着36个价值不等的礼物,每个小的棋盘上面放置着一个礼物,他需要从左上角开始游戏,每次只能向下或者向右移动一步,到达右下角停止,一路上的格子里的礼物小东都能拿到,请设计一个算法使小东拿到价值最高的礼物。 给定一个6*6的矩阵board,其中每个元素为对应格子的礼物价值,左上角为[0,0],请返回能获得的最大价值,保证每个礼物价值大于100小于1000。 动规划基本题 ''' ''' [编程题] 小东分苹果 时间限制:3秒 空间限制:32768K 果园里有一堆苹果,一共n头(n大于1小于9)熊来分,第一头为小东,它把苹果均分n份后,多出了一个,它扔掉了这一个,拿走了自己的一份苹果,接着第二头熊重复这一过程,即先均分n份,扔掉一个然后拿走一份,以此类推直到最后一头熊都是这样(最后一头熊扔掉后可以拿走0个,也算是n份均分)。问最初这堆苹果最少有多少个。 给定一个整数n,表示熊的个数,返回最初的苹果数。保证有解。 测试样例: 2 返回:3 #最后的熊拿之前显然有一个苹果,这样最好 倒数第二个熊是,last*(n)/(n-1)+1 # -*- coding:utf-8 -*- class Apples: def getInitial(self, n): # write code here a=n for k in range(99999): out=1+k*a #out表示最后一个熊拿之前的苹果数. for i in range((a-1)): if int(out*a/(a-1))!=out*a/(a-1): break out=out*a//(a-1)+1 else: return out a=Apples() print(a.getInitial(6)) ''' ''' python2 class Apples: def getInitial(self, n): # write code here a=n for k in range(99999): out=1+k*a #out表示最后一个熊拿之前的苹果数. for i in range((a-1)): if int(out*a/(a-1+0.0))!=out*a/(a-1+0.0): break out=out*a/(a-1)+1 else: return out ''' ''' 链接:https://www.nowcoder.com/questionTerminal/532d89889b974506a0805062fd1089fb 来源:牛客网 import java.util.*; /**思路:因为每次分n堆都会多出来1个,所以我们借给熊n-1个,以致每次都可以刚好分成n堆*/ public class Apples { public int getInitial(int n) { long a = (long)Math.pow(n, n); return (int)a-n+1; } } ''' ''' 所以python代码可以写: # -*- coding:utf-8 -*- class Apples: def getInitial(self, n): # write code here return n**n-n++1 ''' ''' 继续做京东的题目: [编程题] 保卫方案 时间限制:2秒 空间限制:65536K 战争游戏的至关重要环节就要到来了,这次的结果将决定王国的生死存亡,小B负责首都的防卫工作。首都位于一个四面环山的盆地中,周围的n个小山构成一个环,作为预警措施,小B计划在每个小山上设置一个观察哨,日夜不停的瞭望周围发生的情况。 一旦发生外地入侵事件,山顶上的岗哨将点燃烽烟,若两个岗哨所在的山峰之间没有更高的山峰遮挡且两者之间有相连通路,则岗哨可以观察到另一个山峰上的烽烟是否点燃。由于小山处于环上,任意两个小山之间存在两个不同的连接通路。满足上述不遮挡的条件下,一座山峰上岗哨点燃的烽烟至少可以通过一条通路被另一端观察到。对于任意相邻的岗哨,一端的岗哨一定可以发现一端点燃的烽烟。 小B设计的这种保卫方案的一个重要特性是能够观测到对方烽烟的岗哨对的数量,她希望你能够帮她解决这个问题。 输入描述: 输入中有多组测试数据,每一组测试数据的第一行为一个整数n(3<=n<=10^6),为首都周围的小山数量,第二行为n个整数,依次表示为小山的高度h(1<=h<=10^9). 输出描述: 对每组测试数据,在单独的一行中输出能相互观察到的岗哨的对数。 输入例子1: 5 1 2 4 5 3 输出例子1: 7 ''' ''' 尽管是一个CS专业的学生,小B的数学基础很好并对数值计算有着特别的兴趣,喜欢用计算机程序来解决数学问题,现在,她正在玩一个数值变换的游戏。她发现计算机中经常用不同的进制表示一个数,如十进制数123表达为16进制时只包含两位数7、11(B),用八进制表示为三位数1、7、3,按不同进制表达时,各个位数的和也不同,如上述例子中十六进制和八进制中各位数的和分别是18和11,。 小B感兴趣的是,一个数A如果按2到A-1进制表达时,各个位数之和的均值是多少?她希望你能帮她解决这个问题? 所有的计算均基于十进制进行,结果也用十进制表示为不可约简的分数形式。 反复算mod就行了 #一个数字按不同进制的各个位加和,反复取mod n=123 def main(n,k): cnt=0 while n!=0: cnt+=n%k #余的数就是我们要的,进制转换算法,就是不停的取mod,算完一个写到最低位. #一直到被除数是0就停止. n=n//k return cnt print(main(123,16)) ''' ''' [编程题] 神奇数 时间限制:1秒 空间限制:32768K 东东在一本古籍上看到有一种神奇数,如果能够将一个数的数字分成两组,其中一组数字的和等于另一组数字的和,我们就将这个数称为神奇数。例如242就是一个神奇数,我们能够将这个数的数字分成两组,分别是{2,2}以及{4},而且这两组数的和都是4.东东现在需要统计给定区间中有多少个神奇数,即给定区间[l, r],统计这个区间中有多少个神奇数,请你来帮助他。 输入描述: 输入包括一行,一行中两个整数l和r(1 ≤ l, r ≤ 10^9, 0 ≤ r - l ≤ 10^6),以空格分割 输出描述: 输出一个整数,即区间内的神奇数个数 输入例子1: 1 50 输出例子1: 4 写一个判断是否是神奇数的函数,然后遍历.这个题目的取值范围写大了.没有1e9这么多 def main(k): save=[] while k!=0: save.append(k%10) k=k//10 # 下面就是判断这个save数组是否能拆成2块和一样的.背包问题 a=sum(save) if a%2==0: half=sum(save)//2 # 是否能拼成half dp =[[0]*(half+1) for _ in range(len(save))] #dp[i][j]表示用到index i,背包空闲为j,最高放的重量 for i in range(len(save)): for j in range((half+1)): if j<save[i]: dp[i][j]=dp[i-1][j] else: dp[i][j]=max(dp[i-1][j],dp[i-1][j-save[i]]+save[i]) return half in dp[-1] else: return False l,r=map(int,input().split()) cnt=0 for i in range(l,r+1): if main(i): cnt+=1 print(cnt) ''' ''' [编程题] 求幂 时间限制:1秒 空间限制:32768K 东东对幂运算很感兴趣,在学习的过程中东东发现了一些有趣的性质: 9^3 = 27^2, 2^10 = 32^2 东东对这个性质充满了好奇,东东现在给出一个整数n,希望你能帮助他求出满足 a^b = c^d(1 ≤ a,b,c,d ≤ n)的式子有多少个。 例如当n = 2: 1^1=1^1 1^1=1^2 1^2=1^1 1^2=1^2 2^1=2^1 2^2=2^2 一共有6个满足要求的式子 输入描述: 输入包括一个整数n(1 ≤ n ≤ 10^6) 输出描述: 输出一个整数,表示满足要求的式子个数。因为答案可能很大,输出对1000000007求模的结果 输入例子1: 2 输出例子1: 6 #为什么这个题目跟公约数有关???? ''' ''' //这个才是正确的代码 作者:牛妹 链接:https://www.nowcoder.com/discuss/38889?type=0&order=3&pos=6&page=1 来源:牛客网 我们考虑去枚举n范围内的所有i,然后处理出i的幂那些数。 这个i就叫做底. 因为a^b=c^d 那么必然存在一个i s.t.下面的十字成立.这个证明做因数分解即可. 考虑对于i ^ x, 我们需要计算满足 (i ^ x) ^ c = (i ^ y) ^ d的数量,其中i ^ x, i ^ y <= n. 这些我们可以通过预处理出来。 然后对于(i ^ x) ^ c = (i ^ y) ^ d 其实意味着x c = y d, 意味着(x / y) = (d / c),(因为c,d可以做到互素) 其中x, y我们可以在预处理之后枚举出来,于是我们就可以借此计算出n范围内有多少不同这种c和d去满足等式。 其实就等于 n / max(x / gcd(x, y), y / gcd(x, y)),然后都累加进答案。gcd()表示最大公约数。 中间可能产生重复枚举,我们用一个set或者hash容器标记一下就好。 以上枚举对于2~sqrt(n)。最后对于大于sqrt(n)的部分,每个的贡献都是n。 import java.util.HashSet; import java.util.Scanner; import java.util.Set; public class Main { public final static long MOD = 1000000000 + 7; public static int max(int a, int b){ return (a>b) ? a : b; } public static long gcd(long a,long b){ return (a % b == 0) ? b : gcd(b,a%b); } public static void main(String[] args) { Scanner in = new Scanner(System.in); long n = in.nextInt(); long ans = (long)1*n*(2*n-1) % MOD;//以1为底的个数,这个计算方式是 1.计算1**x=1**y 有n**2个 2.计算x**y=x**y这个有 n**2-n个 减去这个n表示第一种1里面1为底的已经算过了. //3.所以下面讨论的情况是(i ^ x) ^ c = (i ^ y) ^ d且x!=y且i>1 这种情况.所以i从2取到根号n. Set<Integer> set = new HashSet<>(); for (int i = 2; i*i <= n; i++){ //下面的底至少是2,指数至少也是2,所以i**2<=n if ( set.contains(i)) continue; long tmp = i; int cnt = 0; while(tmp <= n) { set.add((int)tmp); tmp = tmp * i; cnt++; }//比如i取2,n=10的时候,那么set就是{2,4,8} cnt=3,之后4,8就不用算了,因为他们属于2这个底 //cnt表示最高能取多少次幂. for(int k = 1; k <= cnt; k++) { for(int j = k + 1; j <= cnt; j++) { ans = (ans + n / (j / gcd(k, j) ) * (long)2 ) % MOD; //(j / gcd(k, j) )这个操作就是把k,j这个分数变成互素的. //比如k取1,j取2的时候,ans=ans+10/2*2:因为(i ^ x) ^ c = (i ^ y) ^ d且x!=y且i>1 所以这时也就是 (i ^ 1) ^ c = (i ^ 2) ^ d ,那么d最高取5个数分别是1到5,因为c<=10 //又如k=2,j=3, (i ^ 2) ^ c = (i ^ 3) ^ d ,那么d最高取3个分别是2,4,6,因为c<=10 //这个地方为什么这么计算呢因为k,j互素化之后,为了乘积xk=jy,那么x必须是j的倍数,但是x必须小于n //所以x的取法只有n/j种.(这时j已经是(j / gcd(k, j) )了!) } } } System.out.println(ans); } } --------------------- 作者:生命奇迹泉 来源:CSDN 原文:https://blog.csdn.net/shengmingqijiquan/article/details/77899446?utm_source=copy 版权声明:本文为博主原创文章,转载请附上博文链接! ''' ''' sql语句:删除表属于DDL 用的是drop 删除表中数据 是DML 用的是delete 在关系代数运算中,五种基本运算为()。 正确答案: C 你的答案: D (错误) 并、差、选择、投影、自然连接 并、差、交、选择、投影 并、差、选择、投影、乘积 并、差、交、选择、乘积 OSI是开放式系统互连,由ISO制定,按功能可分为物理层、数据链路层、网络层、传输层、会话层、表示层和应用层共七层 在数据库的数据模型中有()。 网状模型、层次模型、关系模型 0-100的N个数(数的值范围为0~100 1 < N <= 1000),分成两组A、B:怎样分|meanA-meanB|最大? 排序后前50一组,后50一组 ''' ''' [编程题] 解码 时间限制:1秒 空间限制:65536K 有一种将字母编码成数字的方式:'a'->1, 'b->2', ... , 'z->26'。 现在给一串数字,给出有多少种可能的译码结果。 输入描述: 编码后数字串 输出描述: 可能的译码结果数 输入例子1: 12 输出例子1: 2 例子说明1: 2种可能的译码结果(”ab” 或”l”) 输入例子2: 31717126241541717 输出例子2: 192 例子说明2: 192种可能的译码结果 a=input() memo={} def main(a):#返回a有多少种编码结果 if a in memo: return memo[a] if a=='0': return 0 if len(a)==0: return 1 if len(a)==1: return 1 tmp=a[:2] hou=a[2:] if int(tmp)==10: return main(hou) if int(tmp)==20: return main(hou) if int(tmp)<27: case1=main(a[1:]) case2=main(a[2:]) memo[a]=case1+case2 return memo[a] else: case1=main(a[1:]) memo[a]=case1 return memo[a] if a=='0': print(0) else: print(main(a)) ''' ''' [编程题] water 时间限制:1秒 空间限制:131072K 给定四个空杯子,容量分别为S1 S2 S3 S4,允许进行以下操作: 1. 将某个杯子接满水 2. 将某个杯子里的水全部倒掉 3. 将杯子A中的水倒进杯子B,直到A倒空或者B被倒满 问最少要多少步操作才能使得这四个杯子装的水分别为T1 T2 T3 T4 输入描述: 第一行四个非负整数S1 S2 S3 S4 第二行四个非负整数T1 T2 T3 T4 输出描述: 最少的步数,若无法完成则输出-1 输入例子1: 0 2 3 4 0 1 2 4 输出例子1: 6 例子说明1: 过程如下: (0,0,0,0)->(0,2,0,0)->(0,2,3,0)->(0,2,0,3)->(0,0,2,3)->(0,2,2,3)->(0,1,2,4) ''' ''' #include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<bitset> using namespace std; bitset<17043521> Hash; const int MAX_STEP = 100000; int WQ[MAX_STEP][6]; int Goal[5]; int Cap[5]; int goalval; int head = 0; int tail = 0; void movw(int numfrom, int numto, int other1, int other2, int other3) { int total = WQ[head][numfrom] + WQ[head][numto]; WQ[tail][other1] = WQ[head][other1]; WQ[tail][other2] = WQ[head][other2]; WQ[tail][other3] = WQ[head][other3]; WQ[tail][5] = WQ[head][5] + 1; if (total>Cap[numto]) { WQ[tail][numfrom] = total - Cap[numto]; WQ[tail][numto] = Cap[numto]; } else { WQ[tail][numfrom] = 0; WQ[tail][numto] = total; } int hashval = WQ[tail][1] * 262144 + WQ[tail][2] * 4096 + WQ[tail][3] * 64 + WQ[tail][4]; if (hashval == goalval) throw WQ[head][5] + 1; if (!Hash[hashval]) { Hash[hashval] = true; if (++tail == MAX_STEP) tail = 0; } } int main() { Hash.reset(); scanf("%d %d %d %d", &Cap[1], &Cap[2], &Cap[3], &Cap[4]); scanf("%d %d %d %d", &Goal[1], &Goal[2], &Goal[3], &Goal[4]); head = 0; tail = 0; goalval = Goal[1] * 262144 + Goal[2] * 4096 + Goal[3] * 64 + Goal[4]; if (Goal[1] == 0 && Goal[2] == 0 && Goal[3] == 0 && Goal[4] == 0) { printf("0"); return 0; } Cap[0] = 6400; WQ[tail][0] = 6400; WQ[tail][1] = 0; WQ[tail][2] = 0; WQ[tail][3] = 0; WQ[tail][4] = 0; WQ[tail][5] = 0; ++tail; try { while (head != tail) { if (WQ[head][0]) { if (Cap[1]) movw(0, 1, 2, 3, 4); if (Cap[2]) movw(0, 2, 1, 3, 4); if (Cap[3]) movw(0, 3, 1, 2, 4); if (Cap[4]) movw(0, 4, 1, 2, 3); } if (WQ[head][1]) { if (Cap[0]) movw(1, 0, 2, 3, 4); if (Cap[2]) movw(1, 2, 0, 3, 4); if (Cap[3]) movw(1, 3, 0, 2, 4); if (Cap[4]) movw(1, 4, 0, 2, 3); } if (WQ[head][2]) { if (Cap[0]) movw(2, 0, 1, 3, 4); if (Cap[1]) movw(2, 1, 0, 3, 4); if (Cap[3]) movw(2, 3, 0, 1, 4); if (Cap[4]) movw(2, 4, 0, 1, 3); } if (WQ[head][3]) { if (Cap[0]) movw(3, 0, 1, 2, 4); if (Cap[1]) movw(3, 1, 0, 2, 4); if (Cap[2]) movw(3, 2, 0, 1, 4); if (Cap[4]) movw(3, 4, 0, 1, 2); } if (WQ[head][4]) { if (Cap[0]) movw(4, 0, 1, 2, 3); if (Cap[1]) movw(4, 1, 0, 2, 3); if (Cap[2]) movw(4, 2, 0, 1, 3); if (Cap[3]) movw(4, 3, 0, 1, 2); } if (++head == MAX_STEP) { head = 0; } } printf("-1"); } catch (int step) { printf("%d ", step); } } ''' ''' #include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <bitset> using namespace std; bitset<17043521> Hash; //把ABCD杯子需要的状态抽象为一个值 const int MAX_STEP = 100000; int WQ[MAX_STEP][6];//记录每步操作后0和ABCD的当前容量,最后一个记录操作次数 int Goal[5]; int Cap[5]; int goalval; int head = 0; int tail = 0; void movw(int numfrom, int numto, int other1,int other2,int other3) { int total = WQ[head][numfrom] + WQ[head][numto]; WQ[tail][other1] = WQ[head][other1]; WQ[tail][other2] = WQ[head][other2]; WQ[tail][other3] = WQ[head][other3]; WQ[tail][5] = WQ[head][5] + 1; if (total>Cap[numto]) { WQ[tail][numfrom] = total - Cap[numto]; WQ[tail][numto] = Cap[numto]; } else { WQ[tail][numfrom] = 0; WQ[tail][numto] = total; } int hashval = WQ[tail][1] * 262144 + WQ[tail][2] * 4096 + WQ[tail][3] * 64 + WQ[tail][4]; if (hashval == goalval) throw WQ[head][5] + 1; if (!Hash[hashval])//该次操作之后的状态之前未存在过并记录 { Hash[hashval] = true; if (++tail == MAX_STEP) tail = 0; } } int main() { Hash.reset(); scanf("%d %d %d %d", &Cap[1], &Cap[2], &Cap[3],&Cap[4]); scanf("%d %d %d %d", &Goal[1], &Goal[2], &Goal[3], &Goal[4]); head = 0; tail = 0; goalval = Goal[1] * 262144 + Goal[2] * 4096 + Goal[3]*64+Goal[4]; if (Goal[1] == 0 && Goal[2] == 0 && Goal[3] == 0 && Goal[4] == 0 ) { printf("0"); return 0; } Cap[0] = 6400;//0杯子为足够大的杯子 //初始化0和ABCD杯子当前值 WQ[tail][0] = 6400; WQ[tail][1] = 0; WQ[tail][2] = 0; WQ[tail][3] = 0; WQ[tail][4] = 0; WQ[tail][5] = 0; ++tail; try { while (head != tail) { //A导入B,外层if判断A中当前容量不为零,内层判断B的最大容量不为0 if (WQ[head][0]) { if(Cap[1]) movw(0, 1, 2, 3, 4); if (Cap[2]) movw(0, 2, 1, 3, 4); if (Cap[3]) movw(0, 3, 1, 2, 4); if (Cap[4]) movw(0, 4, 1, 2, 3); } if (WQ[head][1]) { if (Cap[0]) movw(1, 0, 2, 3, 4); if (Cap[2]) movw(1, 2, 0, 3, 4); if (Cap[3]) movw(1, 3, 0, 2, 4); if (Cap[4]) movw(1, 4, 0, 2, 3); } if (WQ[head][2]) { if (Cap[0]) movw(2, 0, 1, 3, 4); if (Cap[1]) movw(2, 1, 0, 3, 4); if (Cap[3]) movw(2, 3, 0, 1, 4); if (Cap[4]) movw(2, 4, 0, 1, 3); } if (WQ[head][3]) { if (Cap[0]) movw(3, 0, 1, 2, 4); if (Cap[1]) movw(3, 1, 0, 2, 4); if (Cap[2]) movw(3, 2, 0, 1, 4); if (Cap[4]) movw(3, 4, 0, 1, 2); } if (WQ[head][4]) { if (Cap[0]) movw(4, 0, 1, 2, 3); if (Cap[1]) movw(4, 1, 0, 2, 3); if (Cap[2]) movw(4, 2, 0, 1, 3); if (Cap[3]) movw(4, 3, 0, 1, 2); } if (++head == MAX_STEP) { head = 0; } } printf("-1"); } catch (int step) { printf("%d ", step); } } ''' ''' 无聊时候可以刷刷 https://www.freecodecamp.cn/ ''' ''' 网易游戏(互娱)-游戏研发/初级游戏研发/平台开发岗部分真题汇总 [编程题] 时钟 时间限制:1秒 空间限制:65536K 注意:本题允许使用C/C++/Java/python进行解答,其他编程语言提交均视作无效处理。 小W有一个电子时钟用于显示时间,显示的格式为HH:MM:SS,HH,MM,SS分别表示时,分,秒。其中时的范围为[‘00’,‘01’…‘23’],分的范围为[‘00’,‘01’…‘59’],秒的范围为[‘00’,‘01’…‘59’]。 #但是有一天小W发现钟表似乎坏了,显示了一个不可能存在的时间“98:23:00”,小W希望改变最少的数字,使得电子时钟显示的时间为一个真实存在的时间,譬如“98:23:00”通过修改第一个’9’为’1’,即可成为一个真实存在的时间“18:23:00”。修改的方法可能有很多,小W想知道,在满足改变最少的数字的前提下,符合条件的字典序最小的时间是多少。其中字典序比较为用“HHMMSS”的6位字符串进行比较。 输入描述: 每个输入数据包含多个测试点。每个测试点后有一个空行。 第一行为测试点的个数T(T<=100)。 每个测试点包含1行,为一个字符串”HH:MM:SS”,表示钟表显示的时间。 输出描述: 对于每个测试点,输出一行。如果钟表显示的时间为真实存在的时间,则不做改动输出该时间,否则输出一个新的”HH:MM:SS”,表示修改最少的数字情况下,字典序最小的真实存在的时间。 输入例子1: 2 19:90:23 23:59:59 输出例子1: 19:00:23 23:59:59 玩字典序的题目. n=int(input()) for i in range(n): str1=input().strip() str2=list(str1) time=str1.split(':') for i in range(len(time)): time[i]=int(time[i]) if time[0]>=24: str2[0]='0' if time[1]>=60: str2[3] = '0' if time[2]>=60: str2[6] = '0' print ("".join(str2)) ''' ''' [编程题] 会话列表 时间限制:1秒 空间限制:32768K 小云正在参与开发一个即时聊天工具,他负责其中的会话列表部分。 会话列表为显示为一个从上到下的多行控件,其中每一行表示一个会话,每一个会话都可以以一个唯一正整数id表示。 当用户在一个会话中发送或接收信息时,如果该会话已经在会话列表中,则会从原来的位置移到列表的最上方;如果没有在会话列表中,则在会话列表最上方插入该会话。 小云在现在要做的工作是测试,他会先把会话列表清空等待接收信息。当接收完大量来自不同会话的信息后,就输出当前的会话列表,以检查其中是否有bug。 输入描述: 输入的第一行为一个正整数T(T<=10),表示测试数据组数。 接下来有T组数据。每组数据的第一行为一个正整数N(1<=N<=200),表示接收到信息的次数。第二行为N个正整数,按时间从先到后的顺序表示接收到信息的会话id。会话id不大于1000000000。 输出描述: 对于每一组数据,输出一行,按会话列表从上到下的顺序,输出会话id。 相邻的会话id以一个空格分隔,行末没有空格。 输入例子1: 3 5 1 2 3 4 5 6 1 100 1000 1000 100 1 7 1 6 3 3 1 8 1 输出例子1: 5 4 3 2 1 1 100 1000 1 8 3 6 num=int(input()) for i in range((num)): a=int(input()) tmp=[int(i)for i in input().split()] out=[] for i in range(len(tmp)): if tmp[i] not in out: out=[tmp[i]]+out else: dex=out.index(tmp[i]) out=[out[dex]]+out[:dex]+out[dex+1:] for i in range(len(out)): out[i]=str(out[i]) print(' '.join(out)) ''' ''' 字符迷阵是一种经典的智力游戏。玩家需要在给定的矩形的字符迷阵中寻找特定的单词。 在这题的规则中,单词是如下规定的: 1. 在字符迷阵中选取一个字符作为单词的开头; 2. 选取右方、下方、或右下45度方向作为单词的延伸方向; 3. 以开头的字符,以选定的延伸方向,把连续得到的若干字符拼接在一起,则称为一个单词。 以图1为例,如果要在其中寻找单词"WORD",则绿色框所标示的都是合法的方案,而红色框所标示的都是不合法的方案。 现在的问题是,给出一个字符迷阵,及一个要寻找的单词,问能在字符迷阵中找到多少个该单词的合法方案。注意合法方案是可以重叠的,如图1所示的字符迷阵,其中单词"WORD"的合法方案有4种。 输入描述: #输入的第一行为一个正整数T,表示测试数据组数。 接下来有T组数据。每组数据的第一行包括两个整数m和n,表示字符迷阵的行数和列数。接下来有m行,每一行为一个长度为n的字符串,按顺序表示每一行之中的字符。再接下来还有一行包括一个字符串,表示要寻找的单词。 数据范围: 对于所有数据,都满足1<=T<=9,且输入的所有位于字符迷阵和单词中的字符都为大写字母。要寻找的单词最短为2个字符,最长为9个字符。字符迷阵和行列数,最小为1,最多为99。 对于其中50%的数据文件,字符迷阵的行列数更限制为最多为20。 输出描述: 对于每一组数据,输出一行,包含一个整数,为在给定的字符迷阵中找到给定的单词的合法方案数。 输入例子1: 3 10 10 AAAAAADROW WORDBBBBBB OCCCWCCCCC RFFFFOFFFF DHHHHHRHHH ZWZVVVVDID ZOZVXXDKIR ZRZVXRXKIO ZDZVOXXKIW ZZZWXXXKIK WORD 3 3 AAA AAA AAA AA 5 8 WORDSWOR ORDSWORD RDSWORDS DSWORDSW SWORDSWO SWORD 输出例子1: 4 16 5 num=int(input()) for i in range((num)): chang,kuan=map(int,input().split()) ditu=[] for h in range((chang)): yihang=[] now=input() for i in now: yihang.append(i) ditu.append(yihang) word=input() #下面就是对于ditu里面找word,经典2维搜索dp问题. #如何写好2维搜索:需要套路!: # 第一步就是构造函数:需要参数至少有chang,kuan,i,j,target,k这5个,必要时候需要一个flag来记录. # 第二部就是判断界线,超界线直接return false#并且写法也是永远不变的 # 第三部是判断target的边界 #第四部直接return 递归 所以前3部边界加最后递归即可. #注意这个题目是一条路走到黑,所以需要些3个函数即可!也算是2维dp的经典题目. def judge1(chang,kuan,i,j,target,k):#棋盘chang*kuan 在位置(i,j)处找是否能拼出target[k:]. if i>=chang or j >=kuan or i<0 or j<0 or ditu[i][j]!=target[k]: return False if k==len(target)-1: return True #以上都是套路模板 return judge1(chang,kuan,i+1,j,target,k+1) def judge2(chang,kuan,i,j,target,k):#棋盘chang*kuan 在位置(i,j)处找是否能拼出target[k:]. if i>=chang or j >=kuan or i<0 or j<0 or ditu[i][j]!=target[k]: return False if k==len(target)-1: return True #以上都是套路模板 return judge2(chang,kuan,i,j+1,target,k+1) def judge3(chang,kuan,i,j,target,k):#棋盘chang*kuan 在位置(i,j)处找是否能拼出target[k:]. if i>=chang or j >=kuan or i<0 or j<0 or ditu[i][j]!=target[k]: return False if k==len(target)-1: return True #以上都是套路模板 return judge3(chang,kuan,i+1,j+1,target,k+1) cnt=0 for i in range((chang)): for j in range((kuan)): if judge1(chang,kuan,i,j,word,0): cnt+=1 if judge2(chang,kuan,i,j,word,0): cnt+=1 if judge3(chang,kuan,i,j,word,0): cnt+=1 print(cnt) 总结:其实写多了这种题目变化很少,套路比较深,对智商要求不高,对编程经验需要比较高而已 10分钟之内搞定,说难题还是那种动态规划类型的题目需要智商高 ''' ''' [编程题] 一封奇怪的信 时间限制:1秒 空间限制:32768K 现在你需要用一台奇怪的打字机书写一封书信。信的每行只能容纳宽度为100的字符,也就是说如果写下某个字符会导致行宽超过100,那么就要另起一行书写 信的内容由a-z的26个小写字母构成,而每个字母的宽度均会事先约定。例如字符宽度约定为[1,2,3,4,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5,5],那么就代表'a'到'd'四个字母的宽度分别是1,2,3,4,而'e'到'z'的宽度均为5 那么按照上述规则将给定内容S书写成一封信后,这封信共有几行?最后一行宽度是多少? 输入描述: 输入为两行: 第一行是存储了每个字符宽度的字符串,包含26个数字,以1个空格分隔,每个数字均小于等于10 第二行是存储了待输入字符的字符串S,字符串S的长度在1到1000之间 输出描述: 输出为信的行数以及最后一行所包含的字符个数,中间以1个空格分隔 输入例子1: 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 helloworld 输出例子1: 1 50 例子说明1: "5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5"规定每个字符宽度为5 "helloworld"是输入的字符串S 由于S共包含10个字符,也即共占用50个字符宽度,因此可以写在同一行 输入例子2: 5 5 5 5 5 5 10 10 10 10 10 10 10 10 10 10 10 10 5 5 5 5 5 5 5 5 hahahahahahahaha 输出例子2: 2 20 例子说明2: "5 5 5 5 5 5 10 10 10 10 10 10 10 10 10 10 10 10 5 5 5 5 5 5 5 5"规定了每个字符宽度 "hahahahahahahaha"是输入的字符串S 由于h宽度为10,a宽度为5,因此'hahahahahahah'占用100字符宽度可以写在第一行,‘aha’写在第二行也即最后一行。因此字符宽度为20 典型的计算机模拟过程的题目,意义不大. ''' ''' [编程题] 糖果谜题 时间限制:1秒 空间限制:32768K 小明是幼儿园的一名老师。某天幼儿园园长给小朋友们每人发一颗糖果,小朋友们拿到后发现有一些同学拿到的糖果颜色和自己相同,有一些同学糖果颜色和自己不同。 假定每个小朋友只知道有多少同学和自己拿到了相同颜色的糖果。 上课后,有一部分小朋友兴奋的把这一结果告诉小明老师,并让小明老师猜一猜,最少有多少同学拿到了糖果。 例如有三个小朋友告诉小明老师这一结果如下: 其中第一个小朋友发现有1人和自己糖果颜色一样,第二个小朋友也发现有1人和自己糖果颜色一样,第三个小朋友发现有3人和自己糖果颜色一样。 第一二个小朋友可互相认为对方和自己颜色相同,比如红色; 第三个小朋友不可能再为红色(否则第一二个小朋友会发现有2人和自己糖果颜色相同),假设他拿到的为蓝色糖果,那么至少还有另外3位同学拿到蓝色的糖果,最终至少有6位小朋友拿到了糖果。 现在请你帮助小明老师解答下这个谜题。 输入描述: 假定部分小朋友的回答用空格间隔,如 1 1 3 输出描述: 直接打印最少有多少位小朋友拿到糖果 如 6 输入例子1: 1 1 3 输出例子1: 6 输入例子2: 0 0 0 输出例子2: 3 例子说明2: 三位小朋友都没发现有人和自己的颜色相同,所以最少的情况就是三位小朋友糖果的颜色均不同 也就是相同数字合并.来判断. tmp=[int(i)for i in input().split()] a=set(tmp) suoyouren=0 for i in a: #比如有5个2那么,每一个2只能跟2个其他2进行配对,所以需要 suoyouren+=(tmp.count(i)+i)//(i+1)*(i+1) #太帅了,居然一下过! print(suoyouren) 还是讲一下思路,就是小朋友配对问题.里面也用到了分宿舍技巧. 比如有5个小朋友多说看到2个人跟自己颜色相同,那么我们需要每3个小朋友分配一个颜色,这样最省颜色,也就达到了小朋友的利用率最高,也就让小朋友的数量最少. 那么5个小朋友,每3个分配一个颜色,还剩下2个小鹏有,但是他们也说看到2个颜色,所以要把5个2补成6个2的情况就可以了.就是这一行:(tmp.count(i)+i)//(i+1)*(i+1) ''' ''' [编程题] 字符串编码 时间限制:1秒 空间限制:32768K 给定一个字符串,请你将字符串重新编码,将连续的字符替换成“连续出现的个数+字符”。比如字符串AAAABCCDAA会被编码成4A1B2C1D2A。 输入描述: 每个测试输入包含1个测试用例 每个测试用例输入只有一行字符串,字符串只包括大写英文字母,长度不超过10000。 输出描述: 输出编码后的字符串 输入例子1: AAAABCCDAA 输出例子1: 4A1B2C1D2A 感觉就是单纯考编程技术而已.设置2个指针,一个start一个now.然后不一样就now-start计数即可. ''' ''' [编程题] 最大和 时间限制:1秒 空间限制:32768K 在一个N*N的数组中寻找所有横,竖,左上到右下,右上到左下,四种方向的直线连续D个数字的和里面最大的值 输入描述: 每个测试输入包含1个测试用例,第一行包括两个整数 N 和 D : 3 <= N <= 100 1 <= D <= N 接下来有N行,每行N个数字d: 0 <= d <= 100 输出描述: 输出一个整数,表示找到的和的最大值 输入例子1: 4 2 87 98 79 61 10 27 95 70 20 64 73 29 71 65 15 0 输出例子1: 193 也就是98+98=193 #也是2维搜索问题 n,d=map(int,input().split()) ditu=[] chang=n kuan=n for i in range((n)): tmp=[int(i)for i in input().split()] ditu.append(tmp) def qiuhe1(chang,kuan,i,j,step):#沿着横着走step步能得到的和 #上来就写边界条件: if i>chang-1 or j>kuan-1 or i<0 or j<0 or step==0: return -float('inf')#因为题目不要长度不够的数!!!!!!!!所以设置负无穷即可. if step==1: return ditu[i][j] return ditu[i][j]+qiuhe1(chang,kuan,i,j+1,step-1) def qiuhe2(chang,kuan,i,j,step):#沿着横着走step步能得到的和 #上来就写边界条件: if i>chang-1 or j>kuan-1 or i<0 or j<0 or step==0: return -float('inf') if step==1: return ditu[i][j] return ditu[i][j]+qiuhe2(chang,kuan,i+1,j,step-1) def qiuhe3(chang,kuan,i,j,step):#沿着横着走step步能得到的和 #上来就写边界条件: if i>chang-1 or j>kuan-1 or i<0 or j<0 or step==0: return -float('inf') if step==1: return ditu[i][j] return ditu[i][j]+qiuhe3(chang,kuan,i+1,j+1,step-1) def qiuhe4(chang,kuan,i,j,step):#沿着横着走step步能得到的和 #上来就写边界条件: if i>chang-1 or j>kuan-1 or i<0 or j<0 or step==0: return -float('inf') if step==1: return ditu[i][j] return ditu[i][j]+qiuhe4(chang,kuan,i+1,j-1,step-1) maxi=0 for i in range((chang)): for j in range((kuan)): maxi=max(maxi,qiuhe1(chang,kuan,i,j,d),qiuhe2(chang,kuan,i,j,d),qiuhe3(chang,kuan,i,j,d),qiuhe4(chang,kuan,i,j,d)) print(maxi) ''' ''' [编程题] 推箱子 时间限制:1秒 空间限制:32768K 大家一定玩过“推箱子”这个经典的游戏。具体规则就是在一个N*M的地图上,有1个玩家、1个箱子、1个目的地以及若干障碍,其余是空地。玩家可以往上下左右4个方向移动,但是不能移动出地图或者移动到障碍里去。如果往这个方向移动推到了箱子,箱子也会按这个方向移动一格,当然,箱子也不能被推出地图或推到障碍里。当箱子被推到目的地以后,游戏目标达成。现在告诉你游戏开始是初始的地图布局,请你求出玩家最少需要移动多少步才能够将游戏目标达成。 输入描述: 每个测试输入包含1个测试用例 第一行输入两个数字N,M表示地图的大小。其中0<N,M<=8。 接下来有N行,每行包含M个字符表示该行地图。其中 . 表示空地、X表示玩家、*表示箱子、#表示障碍、@表示目的地。 每个地图必定包含1个玩家、1个箱子、1个目的地。 输出描述: 输出一个数字表示玩家最少需要移动多少步才能将游戏目标达成。当无论如何达成不了的时候,输出-1。 输入例子1: 4 4 .... ..*@ .... .X.. 6 6 ...#.. ...... #*##.. ..##.# ..X... .@#... 输出例子1: 3 11 ''' ''' [编程题] 赛马 时间限制:1秒 空间限制:32768K 在一条无限长的跑道上,有N匹马在不同的位置上出发开始赛马。当开始赛马比赛后,所有的马开始以自己的速度一直匀速前进。每匹马的速度都不一样,且全部是同样的均匀随机分布。在比赛中当某匹马追上了前面的某匹马时,被追上的马就出局。 请问按以上的规则比赛无限长的时间后,赛道上剩余的马匹数量的数学期望是多少 输入描述: 每个测试输入包含1个测试用例 输入只有一行,一个正整数N 1 <= N <= 1000 输出描述: 输出一个浮点数,精确到小数点后四位数字,表示剩余马匹数量的数学期望 输入例子1: 1 2 输出例子1: 1.0000 1.5000 #看看数学上如何分析的,第i快的马货到最后概率是1/i+1 把马的速度设置为0到1之间的实数. 1.看每个马对于最后期望的贡献是多少? 2.最快的马显然是1 3.第二块的马,那么假设他的位置距离原点是x.初始位置是0到1的实数, 那么只有当最快的马在他前面他才能贡献期望1,否则贡献0.所以是(1-x)从0到1做积分.得到1/2 4........类似分析即可答案是调和级数. n = int(raw_input()) res = 0 for i in range(n): res += 1.0/(i+1) print r"%.4f" %res ''' ''' 倒水问题:这个题目的版本非常之多,有微软版的,腾讯版的,新浪版的等等,最常见的是给你一个容量为5升的桶和一个容量为3升的桶,水不限使用,要求精确得到4升水。 倒2次就完事了. [问题]有两个容桶,小桶的容量是4升,大桶的容量是9升,怎样才能从河中恰好打上6升水呢? 先大桶中弄好1升,然后给小桶,之后大桶从9开始给小桶即可. ''' ''' 为了解决倒水问题:先从基础抓起: 倒水问题 总时间限制: 1000ms 内存限制: 65536kB 描述 有三个分别容量分别为a升、b升和c升的杯子(a>b>c>0,且b与c互质)。 a杯装满水,b与c均为空。 三个筒相互倒水且不准把水倒往三个筒之外。 请用最少的倒水次数,倒出d升水(任一杯中正好水量为d 即可),并输出倒水的过程。 输入 只有一行:a、b、c、d 四个整数。 输出 第一行为倒水过程的总步骤 N ,其后N行为倒水的过程; 若无解,则输出“No find”。 样例输入 10 7 3 4 样例输出 3 10 0 0 3 7 0 3 4 3 明显的广搜,这里把vector、queue、stack都用了一遍 --------------------- 作者:zjc_617445 来源:CSDN 原文:https://blog.csdn.net/hsfz_zjc/article/details/75005668 版权声明:本文为博主原创文章,转载请附上博文链接! #include <cstdio> #include <queue> #include <stack> #include <vector> #include <algorithm> #include <iostream> #include <cstdlib> using namespace std; //结构体 struct node { int v[3]; int f; }; //全局变量 const int maxn=200+5; int a,b,c,d; bool tf[maxn][maxn]; int cap[3]; vector <node> vec; bool isok(int i) //判断是否倒水已经成功 { return vec[i].v[0]==d||vec[i].v[1]==d||vec[i].v[2]==d; } void out(int i) { int j; stack<int> sta; do { sta.push(i); if(vec[i].f!=i) i=vec[i].f; else break; }while(1) ; printf("%d ",sta.size() ); while(!sta.empty()) { j=sta.top() ;sta.pop() ; printf("%d %d %d ",vec[j].v[0],vec[j].v[1],vec[j].v[2]); } } void work(int a,int b,int c,int d) { //初始化 for(int i=0;i<maxn;i++) for(int j=0;j<maxn;j++) tf[i][j]=false; vec.clear() ; //准备 queue<int> que; int curr,ii; cap[0]=a; cap[1]=b; cap[2]=c; node s; if(a<d) { printf("No find");return; } s.v[0]=a;s.v[1]=0;s.v[2]=0;s.f =0; vec.push_back(s); if(isok(0)) { printf("1 %d 0 0",a);return; } tf[a][0]=true; que.push(0); //开始 while(!que.empty()) { curr=que.front(); que.pop() ; for(int i=0;i<3;i++) for(int j=0;j<3;j++) { //i->j // printf("** "); if(i==j||vec[curr].v[i]==0||vec[curr].v[j]==cap[j]) continue; // printf("44 "); ii=min(cap[j]-vec[curr].v[j],vec[curr].v[i]); s.f =curr; for(int o=0;o<3;o++) s.v [o]=vec[curr].v[o]; s.v[i]-=ii; s.v[j]+=ii; if(!tf[s.v[0]][s.v[1]]) { tf[s.v[0]][s.v[1]]=true; vec.push_back(s); if(isok(vec.size()-1)) { out(vec.size()-1); return; } que.push(vec.size() -1) ; } } } printf("No find"); } int main() { scanf("%d%d%d%d",&a,&b,&c,&d); work(a,b,c,d); return 0; } ''' ''' 题目要求 有两个容器,容积分别为A升和B升,有无限多的水,现在需要C升水。 我们还有一个足够大的水缸,足够容纳C升水。起初它是空的,我们只能往水缸里倒入水,而不能倒出。 可以进行的操作是: 把一个容器灌满; 把一个容器清空(容器里剩余的水全部倒掉,或者倒入水缸); 用一个容器的水倒入另外一个容器,直到倒出水的容器空或者倒入水的容器满。 问是否能够通过有限次操作,使得水缸最后恰好有C升水。 输入:三个整数A, B, C,其中 0 < A , B, C <= 1000000000 输出:0或1,表示能否达到要求。 函数头部: c语言:1表示可以,0表示不可以 int can(int a,int b,int c); c++语言: true表示可以,false表示不可以 bool can(int a,int b,int c); java语言:true表示可以,false表示不可以 public class Main { public static boolean can(int a,int b,int c); } 解题思路 自己分析: 比如按照大小顺序是a,b 那么可以拼出(ax-by) 这个恰好是最大公约数的公式,所以知道最大公约数可以被拼出来.从而公约数的倍数也是一样表达, 所以一样可以拼出来.那么需要证明的是不是最大公约数的倍数一定拼不出来! 证明:从倒水过程可以看出来能拼出来的数,算上倒掉的水.总体一定是ax+by.因为每一次加水都是加a或者加b,(因为杯子没有刻度).那么每一次倒掉的水也一定是a或者b的倍数.所以最后剩下的水也是ax+by. 所以显然是最大公约数的倍数.所以判断一个target是否能倒出来,只需要判断他是否是最大公钥数的倍数即可. 这是一个典型的倒水问题/量水问题,使用欧几里得算法就可解出来。 这里有一篇文章给出了简单的倒水问题的解法,可以解决笔试面试里面一些简单的填空题,可以看一看:http://blog.csdn.net/morewindows/article/details/7481851 基本思想是:不断用小桶装水倒入大桶,大桶满了立即清空,每次判断下二个桶中水的容量是否等于指定容量。也就是用小桶容量的倍数对大桶的容量进行取余,直到余数等于指定容量。 例如,用7升的桶和11升的桶得到2升水可以这样做: 7 % 11 = 7 14 % 11 = 3 21 % 11 = 10 28 % 11 = 6 35 % 11 = 2 成功得到2升水。 对于明确说明可以得到xx升水,需要我们给出如何倒出来的步骤,可以用这个方法,很快捷。但是这个方法不适合解这道题。 欧几里德算法又称辗转相除法,用于计算两个正整数a,b的最大公约数。 用gcd(a,b) 表示a, b的最大公约数,则有定理:gcd(a,b) = gcd(b,a mod b) (a>b 且a mod b 不为0) 具体的算法实现有循环和递归两种,我用的是循环的方法。 扩展欧几里得算法 定理:对于不完全为 0 的非负整数 a,b,gcd(a, b)表示 a, b 的最大公约数,必然存在整数对 x, y ,使得 gcd(a,b)=ax+by。 本题实际上是问是否存在整数x, y,使得ax+by=c成立。如果c可以被gcd(a,b)整除,则成立。 因此解题步骤如下: 1. 求出gcd(a,b) 2. 判断c是否能被gcd(a,b)整除,若能则返回true,否则返回false ''' ''' dfs:倒水 #这个题目看起来好像是一道模拟题,其实不然,这是一道dfs搜索题,只不过看起来好像无从下手,其实想想就好了,我们可以用一个vis数组来保存当前的状态如果之前某一次倒水出现过这种情况,我们就无需再次去遍历这种情况,只需要遍历其他情况就好了,还有一个重要的剪枝就是假如说我们已经找到某一种情况可以到达目标状态,那么深度再深的我们就无需再次去遍历,因为绝对不是最优解。 --------------------- 作者:caojiangxia 来源:CSDN 原文:https://blog.csdn.net/caojiangxia/article/details/46341005 版权声明:本文为博主原创文章,转载请附上博文链接! 抄点歌曲 [原][歌曲]感动的歌曲排序 故事: 起风了 买辣椒也用券 《起风了》情感历程 成长: 木马城市 毛不易 男孩长大为人 感悟: 在人间 王建房 爱情: 你还要我怎样 薛之谦 分手后的怀念 非常非常精彩的dp问题!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! 理解了一点dp的本质就是函数递归,写好函数,然后递归调用.期间用动态规划. 注意flag的使用,和递归出来一般需要flag归位!!!!!!!!!! //当然这种题目也是,弄个几千或者几万直接就炸.毕竟np hard问题. #include<cstdio> #include<cstring> int a,b,c,t,vis[105][105];//题目:用a,b两个杯子如何倒出c这么多的水 //t表示深度,如果深度大于t就停止dp char s[205][15],s2[205][15],choice[][10]={"FILL(1)","FILL(2)","DROP(1)","DROP(2)","POUR(1,2)","POUR(2,1)"}; void dfs(int n,int m,int deep){ int dn,dm,i,j; if(deep>=t) return; //如果其中一个水杯已经满足有c单位的水就成功,所以这时候就让全局变量t设置为deep if(n==c||m==c){ t=deep; for(i=0;i<t;i++) strcpy(s2[i],s[i]);//把s的所有操作都给s2,作为保存 } //下面是6种操作分类讨论. strcpy(s[deep],choice[0]);//表示当前方法的第deep步使用的方法是choice[0] if(!vis[a][m]){//因为操作0是fill(1),所以得到的结果是第一个杯子满了是a,第二个杯子是m vis[a][m]=1;//表示进入 dfs(a,m,deep+1);//出来递归的时候,把这个flag再变回去,所以下面一行再设置为未访问. //非常牛逼的思路.当然比较朴素,但是我就是dp垃圾,感觉还是8皇后问题理解不够.自己想不到dp思路. vis[a][m]=0; } // strcpy(s[deep],choice[1]); if(!vis[n][b]){ vis[n][b]=1; dfs(n,b,deep+1); vis[n][b]=0;//递归出来一般需要flag归位!!!!!!!!!! } strcpy(s[deep],choice[2]); if(!vis[0][m]){ vis[0][m]=1; dfs(0,m,deep+1); vis[0][m]=0; } strcpy(s[deep],choice[3]); if(!vis[n][0]){ vis[n][0]=1; dfs(n,0,deep+1); vis[n][0]=0; } strcpy(s[deep],choice[4]); if(b-m>=n){ dn=0; dm=m+n; } else { dn=n-(b-m); dm=b; } if(!vis[dn][dm]){ vis[dn][dm]=1; dfs(dn,dm,deep+1); vis[dn][dm]=0; } strcpy(s[deep],choice[5]); if(a-n>=m){ dm=0; dn=m+n; }//不够倒满第一个杯子,所以第一个杯子m+n第二杯0 else { dm=m-(a-n); dn=a; }//够倒满所以第一个杯子a,第二个杯子m-a+n if(!vis[dn][dm]){ vis[dn][dm]=1; dfs(dn,dm,deep+1); vis[dn][dm]=0; } } int main(void){ int i; while(scanf("%d %d %d",&a,&b,&c)!=EOF){ t=1000000000; memset(vis,0,sizeof(vis)); dfs(0,0,0); if(t==1000000000) printf("impossible "); else{ printf("%d ",t); for(i=0;i<t;i++) printf("%s ",s2[i]); } } } ''' ''' [编程题] 倒置字符串 时间限制:1秒 空间限制:32768K 将一句话的单词进行倒置,标点不倒置。比如 I like beijing. 经过函数后变为:beijing. like I 输入描述: 每个测试输入包含1个测试用例: I like beijing. 输入用例长度不超过100 输出描述: 依次输出倒置之后的字符串,以空格分割 输入例子1: I like beijing. 输出例子1: beijing. like I a=input().split(' ') a=a[::-1] print(' '.join(a)) ''' ''' [编程题] 删除公共字符 时间限制:1秒 空间限制:32768K 输入两个字符串,从第一字符串中删除第二个字符串中所有的字符。例如,输入”They are students.”和”aeiou”,则删除之后的第一个字符串变成”Thy r stdnts.” 输入描述: 每个测试输入包含2个字符串 输出描述: 输出删除后的字符串 输入例子1: They are students. aeiou 输出例子1: Thy r stdnts. a1=input() a2=input() dex=[] for i in range(len(a1)): for j in range(len(a2)): if a1[i]==a2[j]: dex.append(i) out='' for i in range(len(a1)): if i not in dex: out+=a1[i] print(out) ''' ''' [编程题] 求和 时间限制:1秒 空间限制:32768K 输入两个整数 n 和 m,从数列1,2,3.......n 中随意取几个数,使其和等于 m ,要求将其中所有的可能组合列出来 //注意是取几个数,没说数量. 输入描述: 每个测试输入包含2个整数,n和m 输出描述: 按每个组合的字典序排列输出,每行输出一种组合 输入例子1: 5 5 输出例子1: 1 4 2 3 5 #又没写出来dp问题 [n,m]=[int(x) for x in input().split(' ')] l=[] #之前选的数 #总结这种需要返回分类后的结果的dp问题的思路: #1.先定义一个数组来存结果,因为这种递归问题都是逐步的解答,最后需要拼起来才是答案,所以需要数组2.之后定义函数f(n,m,k) k是开始index 3.对于函数先写边界值.也就是最后的判断输出点.即这个题目就是最后的m==0,就可以输出l了.4进行每一个分类的递归来跑遍.每一次都是先加入解l中跑完后再从l中剔除.跟倒水问题很像!!!!!!! def f(n,m,k): if m==0: print (' '.join(str(x)for x in l)) for i in range(k,n+1): if i>m: break l.append(i) f(n,m-i,i+1) l.pop() f(n,m,1) 自己写的: n,m=map(int,input().split()) l=[] out=[] def main(n,m,k):#k是index if m==0: out.append(l[:]) #注意因为数组的mutable属性.所以这里要复制 for i in range(k,(n)+1): if i>m: break l.append(i) main(n,m-i,k+1) l.pop() main(n,m,1) print(out) ''' ''' [编程题] 字符串中找出连续最长的数字串 时间限制:1秒 空间限制:32768K 读入一个字符串str,输出字符串str中的连续最长的数字串 输入描述: 个测试输入包含1个测试用例,一个字符串str,长度不超过255。 输出描述: 在一行内输出str中里连续最长的数字串。 输入例子1: abcd12345ed125ss123456789 输出例子1: 123456789 ''' ''' [编程题] n个数里最小的k个 时间限制:1秒 空间限制:32768K 找出n个数里最小的k个 输入描述: 每个测试输入包含空格分割的n+1个整数,最后一个整数为k值,n 不超过100。 输出描述: 输出n个整数里最小的k个数。升序输出 输入例子1: 3 9 6 8 -10 7 -11 19 30 12 23 5 输出例子1: -11 -10 3 6 7 ''' ''' [编程题] n个数里出现次数大于等于n/2的数 时间限制:1秒 空间限制:32768K 输入n个整数,输出出现次数大于等于数组长度一半的数。 输入描述: 每个测试输入包含 n个空格分割的n个整数,n不超过100,其中有一个整数出现次数大于等于n/2。 输出描述: 输出出现次数大于等于n/2的数。 输入例子1: 3 9 3 2 5 6 7 3 2 3 3 3 输出例子1: 3 都是水题不写了. ''' ''' [编程题] 幂运算 时间限制:1秒 空间限制:131072K 给定两个数R和n,输出R的n次方,其中0.0<R<99.999, 0<n<=25 输入描述: 多组测试用例,请参考例题的输入处理 输入每行一个浮点数 R 其中0.0 < R <99.999, 一个整数 n 其中0 < n <=25 输出描述: 输出R的n次方 输入例子1: 95.123 12 0.1 1 输出例子1: 548815620517731830194541.899025343415715973535967221869852721 0.1 ''' ''' [编程题] 几个岛 时间限制:1秒 空间限制:65536K 给定一个m行n列的二维地图, 初始化每个单元都是水. 操作addLand 把单元格(row,col)变成陆地. 岛屿定义为一系列相连的被水单元包围的陆地单元, 横向或纵向相邻的陆地称为相连(斜对角不算). 在一系列addLand的操作过程中, 给出每次addLand操作后岛屿的个数. 二维地图的每条边界外侧假定都是水. 输入描述: 多组测试数据,请参考例题处理 每组数据k+3行, k表示addLand操作次数 第一行:表示行数m 第二行:表示列数n 第三行:表示addLand操作次数k 第4~k+3行:row col 表示addLand的坐标。注意超过边界的坐标是无效的。 输出描述: 一行,k个整数, 表示每次addLand操作后岛屿的个数, 用空格隔开,结尾无空格 输入例子1: 3 3 4 0 0 0 1 1 2 2 1 输出例子1: 1 1 2 3 hang=int(input()) lie=int(input()) cishu=int(input()) if hang==0 or lie==0: print('') else: ditu=[[0]*lie for _ in range(hang)] output=[] for i in range((cishu)): a,b=map(int, input().split()) try:#因为有一个测试用例有bug,不在地图范围,所以用try ditu[a][b]=1 except: pass #下面判断当前ditu有几个岛屿,还是dp上下左右遍历. flag=[[0]*lie for _ in range(hang)] cnt=[0]#用这个cnt[0]来记录多少个独立的岛(因为数组是自动全局的所以这样写方便一些) def dp(hang,lie, a,b):#把a,b坐标的能连接岛屿的都设置为1 if a>hang-1 or b>lie-1 or a<0 or b<0 or ditu[a][b]==0 or flag[a][b]==1: return flag[a][b]=1 #判断是不是一个新岛 beixuan=[(a-1,b),(a,b-1),(a+1,b),(a,b+1)] beixuan2=[] for i in range(len(beixuan)): if beixuan[i][0]>hang-1 or beixuan[i][0]<0 or beixuan[i][1]>lie-1 or beixuan[i][1]<0: pass else: beixuan2.append(beixuan[i]) for i in range(len(beixuan2)): if ditu[beixuan2[i][0]][beixuan2[i][1]]==1 and flag[beixuan2[i][0]][beixuan2[i][1]]==1:#周围的点有走过的岛屿就是不是新的 shiNew=0 break else: shiNew=1 if shiNew==1: cnt[0]+=1 dp(hang,lie, a-1,b) dp(hang,lie, a,b-1) dp(hang,lie, a+1,b) dp(hang,lie, a,b+1) return for i in range((hang)): for j in range((lie)): dp(hang,lie,i,j) output.append(cnt[0]) for i in range(len(output)): output[i]=str(output[i]) print(' '.join(output)) ''' ''' 别人写 的上个题目.简练多了 m = int(input()) n = int(input()) k = int(input()) adl = [] for i in range(k): adl.append(map(int,raw_input().split()))#adl是添加过程 matrix是地图 def addland(i, j, m, n, matrix): #i, j = d[0], d[1] if i>=m or j >= n or i<0 or j<0 or matrix[i][j] == 0:return if matrix[i][j] == 1: matrix[i][j] = 0 addland(i+1, j, m, n, matrix) addland(i-1, j, m, n, matrix) addland(i, j+1, m, n, matrix) addland(i, j-1, m, n, matrix) return 1 result = [] for l in range(len(adl)): res = 0 matrix_g = [[0 for i in range(n)] for j in range(m)] for w in adl[:l+1]: if w[0]<m and w[1]<n: matrix_g[w[0]][w[1]] = 1 #matrix_g生成了当前步奏所生成的地图 for i in range(m): for j in range(n): if matrix_g[i][j] == 1: res += addland(i, j, m, n, matrix_g) result.append(str(res)) print ' '.join(result) 看看别人写的.我加上注释.果然牛逼.非常经典的题目,又学了很多技巧.!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! m = int(input()) n = int(input()) k = int(input()) adl = [] for i in range(k): adl.append([int(i)for i in input().split()])#adl是添加过程 matrix是地图 def addland(i, j, m, n, matrix): #i, j = d[0], d[1] if i>=m or j >= n or i<0 or j<0 :return 0 if matrix[i][j] == 1: matrix[i][j] = 0 #下面4步把周围的1变0,所以再访问到1就是一个孤立的岛屿!牛逼,这个太牛逼了. #道理就是比如矩阵[[1, 1], [0, 0]],访问第一个一的时候,就进入递归调用访问addland(0, 1, m, n, matrix),但是调用后不管他返回多少,我都没获得,因为我只回收addland(0, 0, m, n, matrix),但是这部调用把[0,1]坐标的值给修改成0了,所以下次访问就访问不到[0,1]坐标了.从而这个4步递归等效于把岛屿这个点临街的岛屿都给抹杀了.递归下去就是把跟[0,0]相连的岛屿都抹杀,从而下次加的就是新的独立岛屿!虽然短但是牛逼的代码! addland(i+1, j, m, n, matrix) addland(i-1, j, m, n, matrix) addland(i, j+1, m, n, matrix) addland(i, j-1, m, n, matrix) return 1 result = [] for l in range(len(adl)): res = 0 matrix_g = [[0 for i in range(n)] for j in range(m)] for w in adl[:l+1]: if w[0]<m and w[1]<n: matrix_g[w[0]][w[1]] = 1 #matrix_g生成了当前步奏所生成的地图 print(matrix_g) for i in range(m): for j in range(n): if matrix_g[i][j] == 1: res += addland(i, j, m, n, matrix_g) result.append(str(res)) print (' '.join(result)) ''' ''' 首页 题库 学习 求职 讨论区 发现 搜索 APP 消息 44/44 00:03:45 [编程题] CIDR去重 时间限制:1秒 空间限制:65536K #无类别域间路由(CIDR)是一个用于对IPV4地址进行分类表述的方法。CIDR 路由描述的IP地址组的子网mask长度是可变长度, 例如10.0.0.0/22 表示前22位和10.0.0.0相同的网络地址都被覆盖, 22包含了10.0这前两个字段(0-7位,8-15位)和第三个字段的前6位(16-21,即0b000000**), 涵盖了 10.0.0.*, 10.0.1.*, 10.0.2.*, 10.0.3.* 四组ip地址. 在此前提下请实现IP网络中的一个常用的去重操作: 给定一系列 CIDR 路由地址, 其中没有完全等价的路由, 去掉被重复表示的 CIDR 路由, 即去掉已经被其他CIDR路由表示覆盖的路由地址. 例如 10.0.1.1/32 已经被 10.0.0.0/22覆盖了, 如果路由列表中已经有了后者, 就可以去掉前者. 输入描述: k+1行, k表示输入的CIDR路由个数 第1行:表示路由个数k 第2~k+1行: 表示一个CIDR路由, 形如 x.x.x.x/x 输出描述: n+1行, n表示去重后剩下的CIDR路由个数 第1行:n 第2~n+1行: 表示一个去重后的CIDR路由, 输出按照输入顺序 输入例子1: 13 192.168.0.0/16 172.24.96.17/32 172.50.137.225/32 202.139.219.192/32 172.24.68.0/24 192.183.125.71/32 201.45.111.138/32 192.168.59.211/32 192.168.26.13/32 172.24.0.0/17 172.24.5.1/32 172.24.68.37/32 172.24.168.32/32 输出例子1: 7 192.168.0.0/16 172.50.137.225/32 202.139.219.192/32 192.183.125.71/32 201.45.111.138/32 172.24.0.0/17 172.24.168.32/32 ''' ''' [编程题] 最短字符编码 时间限制:1秒 空间限制:65536K 给定一个非空字符串, 按照如下方式编码, 使得编码后长度最小, 返回编码后的长度: 编码规则为: k[encoding_string], 表示重复k次encoding_strng, 例如'abcdefabcdefabc'可表示为'2[abcdef]abc', 但是'aaa'仅能编码成'aaa', 因为len('3[a]')>len('aaa'). 补充: 1. k为正整数, []内的encoding_string不得含有空格不得为空; 2. []内的encoding_string 本身可以为编码过的字符串, 例如'abcdabcdeabcdabcde' 可以编码为 '2[abcdabcde]'(编码后长度从18减少到12), []内的'abcdabcde'又可以编码为 '2[abcd]e', 最终编码为 '2[2[abcd]e]', 编码后长度为11, 应返回11; 这个编码路径也能是: 'abcdabcdeabcdabcde' -> '2[abcd]e2[abcd]e' -> '2[2[abcd]e]'; 2. 输入字符串为全小写英文字母, 长度<=160; 3. 如果编码后长度没有更小, 则保留原有字符串; 输入描述: 一行数据, 表示输入字符串 输出描述: 输出一个字符串表示编码后长度 输入例子1: aaa 输出例子1: 3 例子说明1: aaa,长度3 输入例子2: aaaaa 输出例子2: 4 例子说明2: 5[a],长度4 输入例子3: aabcaabcd 输出例子3: 8 例子说明3: 2[aabc]d,长度8 a=input() memo={} def main(a):#返回a最小能压缩到的结果 if a in memo: return memo[a] new=a mini=len(a) for j in range(len(a)-4):#切分点是j for i in range(1,len(a)//2+1):#长度是i start=0 while a[j:i+j]==a[j+(start+1)*i:j+(start+2)*i]: start+=1 tmp=main(a[:j])+str(start+1)+'['+main(a[j:i+j])+']'+main(a[j+(start+1)*i:]) if len(tmp)<mini: new=tmp mini=len(tmp) memo[a]=new return memo[a] #还需要继续讨论不是从头开始折叠的情况. #print((main(a)) ) print(len(main(a)) )#这么写超时 #通过对下面别人代码的分析,他的memo里面是记录可以压缩才进去,而我的是都放进去,所以他的更节省空间和时间. ''' ''' def check(a, i, j): if i + (j - i) * 2 > len(a): return False, a p, q = i, j adjust = 0 while q <= len(a): if a[p:q] == a[q:q + q - p]: p, q = q, q + q - p adjust = adjust + 1 else: break if adjust > 0: res = a[:i] + str(adjust+1) + '[' + a[i:j] + ']' + a[q:] if len(res) <= len(a): return True, res return False, a def solve(a): res = [len(a)] table = dict() def change(a): if len(a) > 4: for i in range(len(a) - 1): for j in range( i+1,len(a) - 1): c, tmp = check(a, i, j) if c: if len(tmp) < res[0]: res[0] = len(tmp) if tmp not in table: table[tmp] = True change(tmp)#原来是在这里来进行递归操作!!!!!!!!!! change(a) return res[0] if __name__ == "__main__": a = input().strip() print(solve(a)) ''' ''' [编程题] xor 时间限制:1秒 空间限制:65536K 给出n个数字 a_1,...,a_n,问最多有多少不重叠的非空区间,使得每个区间内数字的xor都等于0。 输入描述: 第一行一个整数n; 第二行n个整数 a_1,...,a_n; 对于30%的数据,n<=20; 对于100%的数据,n<=100000, a_i<=100000; 输出描述: 一个整数表示最多的区间个数; 输入例子1: 4 3 0 2 2 输出例子1: 2 题意不懂.直接看答案 n=int(input()) #n=4 A=[] l=raw_input() A=[int(x) for x in l.split()] #3 0 2 2 m={} m[0]=1 r=0 ans=0 for a in A: ans^=a if ans in m: r+=1 m.clear() m[ans]=1 print r ''' ''' [编程题] CIDR去重 时间限制:1秒 空间限制:65536K #无类别域间路由(CIDR)是一个用于对IPV4地址进行分类表述的方法。CIDR 路由描述的IP地址组的子网mask长度是可变长度, 例如10.0.0.0/22 表示前22位和10.0.0.0相同的网络地址都被覆盖, 22包含了10.0这前两个字段(0-7位,8-15位)和第三个字段的前6位(16-21,即0b000000**), 涵盖了 10.0.0.*, 10.0.1.*, 10.0.2.*, 10.0.3.* 四组ip地址. 因为前面22为是网络地址,所以已经确定了.所以是0*....4*这些可以变化. 在此前提下请实现IP网络中的一个常用的去重操作: 给定一系列 CIDR 路由地址, 其中没有完全等价的路由, 去掉被重复表示的 CIDR 路由, 即去掉已经被其他CIDR路由表示覆盖的路由地址. 例如 10.0.1.1/32 已经被 10.0.0.0/22覆盖了, 为什么覆盖了?需要转化成2进制来看 如果路由列表中已经有了后者, 就可以去掉前者. 输入描述: k+1行, k表示输入的CIDR路由个数 第1行:表示路由个数k 第2~k+1行: 表示一个CIDR路由, 形如 x.x.x.x/x 输出描述: n+1行, n表示去重后剩下的CIDR路由个数 第1行:n 第2~n+1行: 表示一个去重后的CIDR路由, 输出按照输入顺序 输入例子1: 13 192.168.0.0/16 172.24.96.17/32 172.50.137.225/32 202.139.219.192/32 172.24.68.0/24 192.183.125.71/32 201.45.111.138/32 192.168.59.211/32 192.168.26.13/32 172.24.0.0/17 172.24.5.1/32 172.24.68.37/32 172.24.168.32/32 输出例子1: 7 192.168.0.0/16 172.50.137.225/32 202.139.219.192/32 192.183.125.71/32 201.45.111.138/32 172.24.0.0/17 172.24.168.32/32 根据分析,用2进制转化后按照长度排序后去重即可.最后按照原始顺序输出即可 num=int(input()) save=[] save3=[] for i in range((num)): tmp=input() a=tmp.split('/')[0] b=int(tmp.split('/')[1]) arr=a.split('.') save.append((arr,b)) save3.append(tmp) save=sorted(save,key=lambda x:x[1]) save2=[] for i in save: arr=i[0] b=str(i[1]) save2.append('.'.join(arr)+'/'+b) #按照长度排序,因为为了避免先判断长的. #转化到2进制 out_dex=[] out=[] for i in range(len(save)): arr=save[i][0] b=save[i][1] for j in range(len(arr)): arr[j]=bin(int(arr[j]))[2:] arr[j]=(8-len(arr[j]))*'0'+arr[j] b=int(b) now=''.join(arr)[:b] for j in out: if now[:len(j)]==j: break else: out.append(now) out_dex.append(i) output=[] for i in out_dex: output.append(save2[i]) print(len(output)) for i in save3: #为了变回之前的顺序. if i in output: print(i) ''' ''' 滴滴出行2017秋招笔试真题-编程题汇总 [编程题] 连续最大和 时间限制:1秒 空间限制:32768K 一个数组有 N 个元素,求连续子数组的最大和。 例如:[-1,2,1],和最大的连续子数组为[2,1],其和为 3 输入描述: 输入为两行。 第一行一个整数n(1 <= n <= 100000),表示一共有n个元素 第二行为n个数,即每个元素,每个整数都在32位int范围内。以空格分隔。 输出描述: 所有连续子数组中和最大的值。 输入例子1: 3 -1 2 1 输出例子1: 3 继续联系基本功. a=int(input()) b=[int(i)for i in input().split()] out=b[0] maxi=b[0] for i in range(1,len(b)): if out<0: out=0 out+=b[i] maxi=max(out,maxi) print(maxi) ''' ''' [编程题] 餐馆 时间限制:1秒 空间限制:65536K 某餐馆有n张桌子,每张桌子有一个参数:a 可容纳的最大人数; 有m批客人,每批客人有两个参数:b人数,c预计消费金额。 在不允许拼桌的情况下,请实现一个算法选择其中一部分客人,使得总预计消费金额最大 输入描述: 输入包括m+2行。 第一行两个整数n(1 <= n <= 50000),m(1 <= m <= 50000) 第二行为n个参数a,即每个桌子可容纳的最大人数,以空格分隔,范围均在32位int范围内。 接下来m行,每行两个参数b,c。分别表示第i批客人的人数和预计消费金额,以空格分隔,范围均在32位int范围内。 输出描述: 输出一个整数,表示最大的总预计消费金额 输入例子1: 3 5 2 4 2 1 3 3 5 3 7 5 9 1 10 输出例子1: 20 贪心法:选人数少,消费高的给最小的桌子. n,m=map(int,input().split()) arr=[int(i)for i in input().split()] keren=[] for i in range(m): keren.append([int(i)for i in input().split()]) keren=sorted(keren,key=lambda x:(x[0],-x[1]))#第一个升序如果相同按照第二个降序 out=0 arr.sort() # print(arr) # print(keren) dex=[] for i in range(len(arr)): tmp_dex=None tmp=0 for j in range(len(keren)): if keren[j][0]<=arr[i] and j not in dex and keren[j][1]>tmp: tmp=keren[j][1] tmp_dex=j # print(99999999999) # print(tmp_dex) dex.append(tmp_dex) newdex=[] for i in range(len(dex)): if dex[i]!=None: newdex.append(dex[i]) dex=newdex # print(newdex) he=0 # print(keren) # print(he) for i in ((newdex)): he+=keren[i][1] print(he) ''' ''' 上面问题完全ac代码.用2分加速查找! import sys #用2分来找index def getindex(data,k):#返回data这个数组中大于=k的最小坐标 i = 0 j = len(data)-1 result=1<<30 while(i<=j): mid = (i+j)//2 if data[mid]>=k: result = min(mid,result) j = mid-1 else: i = mid+1 return result n,m = map(int,input().split()) data = map(int,input().split())#桌子大小 mat = []#客人数据 for i in range(m): mat.append([int(i)for i in input().split()]) data=list(data) data.sort() mat=list(mat) newmat=sorted(mat,key=lambda x:(-x[1],x[0])) #排序按照,消费大的顾客优先.反正:如果消费最大的顾客可以满足,但是你不选他,那么最大的桌子的顾客肯定没有这个消费最大的顾客消费的多,所以如果不选这个消费最大的可以满足他的顾客,那么你得到的解就不是最优的.#所以排序要按照消费排序,当消费一样的时候优先满足要求低的,因为他可以最大限度的节省桌子这个资源. #print(newmat) #print newmat result = 0 #print(data) while(len(data)>0 and len(newmat)>0): num = newmat.pop(0) nums = num[0] #每一次为消费最大的顾客分配一个桌子 k = getindex(data,nums) if k != 1<<30: result+=num[1] data.pop(k) print (result) ''' ''' 按照相同思路自己写一份: import sys #用2分来找index def getindex(data,k):#返回data这个数组中大于=k的最小坐标,如果找不到就返回None first=0 end=len(data)-1 res=1<<30 #大神都用res作为结果 while end-first>1: mid=(first+end)//2 if data[mid]>=k: end=mid res=min(res,end) else: first=mid if data[first]>=k: return first if data[end]>=k: return end return res n,m = map(int,input().split()) data = map(int,input().split())#桌子大小 mat = []#客人数据 for i in range(m): mat.append([int(i)for i in input().split()]) data=list(data) data.sort() mat=list(mat) newmat=sorted(mat,key=lambda x:(-x[1],x[0])) #排序按照,消费大的顾客优先.反正:如果消费最大的顾客可以满足,但是你不选他,那么最大的桌子的顾客肯定没有这个消费最大的顾客消费的多,所以如果不选这个消费最大的可以满足他的顾客,那么你得到的解就不是最优的.#所以排序要按照消费排序,当消费一样的时候优先满足要求低的,因为他可以最大限度的节省桌子这个资源. #print(newmat) #print (newmat) result = 0 #print(data) while(len(data)>0 and len(newmat)>0): num = newmat.pop(0) nums = num[0] #每一次为消费最大的顾客分配一个桌子 k = getindex(data,nums) # print(k) if k != 1<<30: result+=num[1] data.pop(k) print (result) ''' ''' [编程题] 地下迷宫 时间限制:1秒 空间限制:32768K ##小青蛙有一天不小心落入了一个地下迷宫,小青蛙希望用自己仅剩的体力值P跳出这个地下迷宫。为了让问题简单,假设这是一个n*m的格子迷宫,迷宫每个位置为0或者1,0代表这个位置有障碍物,小青蛙达到不了这个位置;1代表小青蛙可以达到的位置。小青蛙初始在(0,0)位置,地下迷宫的出口在(0,m-1)(保证这两个位置都是1,并且保证一定有起点到终点可达的路径),小青蛙在迷宫中水平移动一个单位距离需要消耗1点体力值,向上爬一个单位距离需要消耗3个单位的体力值,向下移动不消耗体力值,当小青蛙的体力值等于0的时候还没有到达出口,小青蛙将无法逃离迷宫。现在需要你帮助小青蛙计算出能否用仅剩的体力值跳出迷宫(即达到(0,m-1)位置)。 输入描述: 输入包括n+1行: 第一行为三个整数n,m(3 <= m,n <= 10),P(1 <= P <= 100) 接下来的n行: 每行m个0或者1,以空格分隔 输出描述: 如果能逃离迷宫,则输出一行体力消耗最小的路径,输出格式见样例所示;如果不能逃离迷宫,则输出"Can not escape!"。 测试数据保证答案唯一 输入例子1: 4 4 10 1 0 0 1 1 1 0 1 0 1 1 1 0 0 1 1 输出例子1: [0,0],[1,0],[1,1],[2,1],[2,2],[2,3],[1,3],[0,3] 非常精彩的题目:是滴滴2017年的笔试题目.相当考验2维map的dp算法. n,m,p=map(int,input().split()) ditu=[] for i in range((n)): ditu.append([int(i)for i in input().split()]) flag=[[0]*m for _ in range(n)] lujing=[] mini=float('inf') save=[1] dic={} #通过立flag来避免循环递归,递归出去再flag回来 def search(n,m,i,j,p):#返回这个点到终点的最好路线,其实就是按照倒水问题套dp算法 #地图n*m 当前位置i,j, 返回当前位置到最终点最好路线需要多少个p值 #p表示从入口到现在消耗的p,因为这个题目需要设置p值,所以比倒水问题难一点应该. lujing.append([i,j]) # print(lujing) if i==0 and j == m-1: #现在拼出最后路径做保存即可 global mini#因为需要修改mini#python对于变量是默认都能访问,但是只有global的才能修改.数组默认global if p<mini: #save=lujing#保存列表不能直接写等,只能用元素赋值来传出去 #下面问题就是怎么把这个传出去,因为数组mutable特性,所以这里别忘了复制列表 #再总结一下这个外界数组跟函数访问修改的问题:函数可以直接访问数组也能修改数组,但是不能用等号来修改数组,字典也同理.对于外界普通变量,函数可以访问变量,但是不能修改变量,想修改只能global. dic[1]=lujing[:] mini=p return if i>n-1 or j>m-1 or i<0 or j<0 or ditu[i][j]==0 or flag[i][j]==1: return flag[i][j]=1 #递归 search(n,m,i-1,j,p+3) lujing.pop() search(n,m,i+1,j,p) lujing.pop() search(n,m,i,j-1,p+1) lujing.pop() search(n,m,i,j+1,p+1) lujing.pop() flag[i][j]=0 search(n,m,0,0,0) out=dic[1] out=str(out) out=out.replace(' ','') if mini<=p: print(out[1:-1]) else: print("Can not escape!") ''' ''' [编程题] 末尾0的个数 时间限制:1秒 空间限制:32768K 输入一个正整数n,求n!(即阶乘)末尾有多少个0? 比如: n = 10; n! = 3628800,所以答案为2 输入描述: 输入为一行,n(1 ≤ n ≤ 1000) 输出描述: 输出一个整数,即题目所求 输入例子1: 10 输出例子1: 2 数有多少个5因子,找完就除5再找(等价于找25的因子)........循环即可. a=int(input()) ans=0 while a!=0: ans+=a//5 a=a//5 print(ans) ''' ''' [编程题] 进制转换 时间限制:1秒 空间限制:32768K 给定一个十进制数M,以及需要转换的进制数N。将十进制数M转化为N进制数 输入描述: 输入为一行,M(32位整数)、N(2 ≤ N ≤ 16),以空格隔开。 输出描述: 为每个测试实例输出转换后的数,每个输出占一行。如果N大于9,则对应的数字规则参考16进制(比如,10用A表示,等等) 输入例子1: 7 2 输出例子1: 111 #算法就是反复取mod m,n=map(int,input().split()) out='' if m<0: #注意32位数表示可以是负数 m=-m while m!=0: tmp=(m%n) if tmp<10: out+=str(tmp) elif tmp==10: out+='A' elif tmp==11: out+='B' elif tmp==12: out+='C' elif tmp==13: out+='D' elif tmp==14: out+='E' elif tmp==15: out+='F' m=m//n print('-'+out[::-1]) else: while m!=0: tmp=(m%n) if tmp<10: out+=str(tmp) elif tmp==10: out+='A' elif tmp==11: out+='B' elif tmp==12: out+='C' elif tmp==13: out+='D' elif tmp==14: out+='E' elif tmp==15: out+='F' m=m//n print(out[::-1]) ''' ''' [编程题] 数字和为sum的方法数 时间限制:1秒 空间限制:32768K 给定一个有n个正整数的数组A和一个整数sum,求选择数组A中部分数字和为sum的方案数。 当两种选取方案有一个数字的下标不一样,我们就认为是不同的组成方案。 输入描述: 输入为两行: 第一行为两个正整数n(1 ≤ n ≤ 1000),sum(1 ≤ sum ≤ 1000) 第二行为n个正整数A[i](32位整数),以空格隔开。 输出描述: 输出所求的方案数 输入例子1: 5 15 5 5 10 2 3 输出例子1: 4 ''' #效率卡的很死,只能用背包问题来写.2维动态规划可以解. ''' 把问题转化为背包重量是sum,物品是arr,有多少种方法放满背包. 这就是01完全背包问题!!!!!!!!!!而不是尽量放背包问题.解答很类似,注意 数组dp[i][j]表示物品是arr[:i] 拼重量是j m,target=map(int,input().split()) arr=[int(i)for i in input().split()] dp=[[0]*(target+1)for _ in range(m+1)]#注意这行的加一操作! dp[0][0]=1#第一行表示用0个物品,最后一行表示用所有物品. for i in range(1,len(dp)): for j in range(len(dp[0])): if i==0 and j==0: continue if arr[i-1]<=j: case1=dp[i-1][j-arr[i-1]] case2=dp[i-1][j] dp[i][j]=case1+case2 else: dp[i][j]=dp[i-1][j] print(dp[-1][-1]) ''' ''' 首页 > 公司真题模考 > 美团点评2017秋招笔试编程题 分享 美团点评2017秋招笔试编程题 企业提供 [编程题] 大富翁游戏 时间限制:1秒 空间限制:32768K 大富翁游戏,玩家根据骰子的点数决定走的步数,即骰子点数为1时可以走一步,点数为2时可以走两步,点数为n时可以走n步。求玩家走到第n步(n<=骰子最大点数且是方法的唯一入参)时,总共有多少种投骰子的方法。 输入描述: 输入包括一个整数n,(1 ≤ n ≤ 6) 输出描述: 输出一个整数,表示投骰子的方法 输入例子1: 6 输出例子1: 32 #也就是解决6能拆成多少个整数的和.但是这个题目输入只有1到6,所以直接递归,不用管效率了 a=int(input()) def main(a):#返回能拼出a的解有多少个 out=0 if a==1: return 1 for i in range(1,(a)): out+=main(i) out+=1 return out print(main(6)) ''' ''' [编程题] 拼凑钱币 时间限制:1秒 空间限制:32768K 给你六种面额 1、5、10、20、50、100 元的纸币,假设每种币值的数量都足够多,编写程序求组成N元(N为0~10000的非负整数)的不同组合的个数。 输入描述: 输入包括一个整数n(1 ≤ n ≤ 10000) 输出描述: 输出一个整数,表示不同的组合方案数 输入例子1: 1 输出例子1: 1 #用记忆递归.过了,但是学习下别人的算法,因为这个空间复杂度太高了 a=int(input()) arr=[1,5,10,20,50,100] memo={} def main(a,k):#用arr前k个元素能拼成a 有多少组合 if (a,k)in memo: return memo[(a,k)] if k==0 and a==0: #只有1块钱 return 1 #这里理解:没有钱的频发不用拼所以也是1种答案,所以返回1!!!!!!!!! if k==0 and a!=0: return 1 out=0 for i in range((a)//arr[k]+1): out+=main(a-i*arr[k],k-1) memo[(a,k)]=out return memo[(a,k)] print(main(a,len(arr)-1)) ''' ''' 还是看别人答案吧,自己写的效率不够 n = int(raw_input()) nums = [0 for i in range(n+1)] coins = [1,5,10,20,50,100] nums[0]=1 for coin in coins: for j in range(coin,n+1): nums[j] = nums[j]+nums[j-coin] print nums[n] ''' ''' [编程题] 字符编码 时间限制:1秒 空间限制:32768K 请设计一个算法,给一个字符串进行二进制编码,使得编码后字符串的长度最短。 输入描述: 每组数据一行,为待编码的字符串。保证字符串长度小于等于1000。 输出描述: 一行输出最短的编码后长度。 输入例子1: MT-TECH-TEAM 输出例子1: 33 看答案 while True: try: s = raw_input() dic = {} for c in s: if c in dic.keys(): dic[c] += 1 else: dic[c] = 1 l = list(dic.values()) res = 0 l.sort() while len(l) > 1:#最小编码算法,haffman算法.每一次找频率最小的2个数加起来.因为他们是最后的叶子,所以只加一次,之后合并再加. l.sort() w = l[0]+l[1] res += w l = l[2:]+[w] print res except: break ''' ''' [编程题] 奇数位丢弃 时间限制:1秒 空间限制:32768K 对于一个由0..n的所有数按升序组成的序列,我们要进行一些筛选,每次我们取当前所有数字中从小到大的第奇数位个的数,并将其丢弃。重复这一过程直到最后剩下一个数。请求出最后剩下的数字。 输入描述: 每组数据一行一个数字,为题目中的n(n小于等于1000)。 输出描述: 一行输出最后剩下的数字。 输入例子1: 500 输出例子1: 255 模拟算法试试,因为n只有1000 while 1: try: a=int(input()) a=range(a) while len(a)>1: b=[] for i in range(len(a)): if i%2!=0: b.append(a[i]) a=b print(a[0]) except: break ''' ''' [编程题] 二维数组打印 时间限制:3秒 空间限制:32768K 有一个二维数组(n*n),写程序实现从右上角到左下角沿主对角线方向打印。 给定一个二位数组arr及题目中的参数n,请返回结果数组。 测试样例: [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]],4 返回:[4,3,8,2,7,12,1,6,11,16,5,10,15,9,14,13] 本质就是沿着对角线切片.看看对角线如何设计算法. 其实不难!果断ac arr=[[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]] a=arr num=len(a) m=len(a) n=len(a[0]) def main(i,j):#把i,j位置的开始的对角线元素生成一个列表 out=[] while i<m and j<n and i>=0 and j>=0: out.append(a[i][j]) i+=1 j+=1 return out new=[] for i in range((n)): new.append(main(0,i)) new=new[::-1] for i in range(1,(n)): new.append(main(i,0)) out=[] for i in range(len(new)): out+=new[i] print(out) ''' ''' tijiao: # -*- coding:utf-8 -*- class Printer: def arrayPrint(self, arr, n): # write code here a=arr num=len(a) m=len(a) n=len(a[0]) def main(i,j):#把i,j位置的开始的对角线元素生成一个列表 out=[] while i<m and j<n and i>=0 and j>=0: out.append(a[i][j]) i+=1 j+=1 return out new=[] for i in range((n)): new.append(main(0,i)) new=new[::-1] for i in range(1,(n)): new.append(main(i,0)) out=[] for i in range(len(new)): out+=new[i] return (out) ''' ''' [编程题] 股票交易日 时间限制:3秒 空间限制:32768K 在股市的交易日中,假设最多可进行两次买卖(即买和卖的次数均小于等于2),规则是必须一笔成交后进行另一笔(即买-卖-买-卖的顺序进行)。给出一天中的股票变化序列,请写一个程序计算一天可以获得的最大收益。请采用实践复杂度低的方法实现。 给定价格序列prices及它的长度n,请返回最大收益。保证长度小于等于500。 测试样例: [10,22,5,75,65,80],6 返回:87 leetcode上的东归题目 ''' ''' [编程题] 最大差值 时间限制:3秒 空间限制:32768K 有一个长为n的数组A,求满足0≤a≤b<n的A[b]-A[a]的最大值。 给定数组A及它的大小n,请返回最大差值。 测试样例: [10,5],2 返回:0 应该是动归,滑动窗口 # -*- coding:utf-8 -*- class LongestDistance: def getDis(self, A, n): res = 0 for i in range(n-1): for j in range(i+1,n): res = max(A[j]-A[i],res) return res a=LongestDistance() print(a.getDis([10,5],2)) 居然这种for循环没写出来......''' ''' ''' ''' [编程题] 棋子翻转 时间限制:3秒 空间限制:32768K 在4x4的棋盘上摆满了黑白棋子,黑白两色的位置和数目随机其中左上角坐标为(1,1),右下角坐标为(4,4),现在依次有一些翻转操作,要对一些给定支点坐标为中心的上下左右四个棋子的颜色进行翻转,请计算出翻转后的棋盘颜色。 给定两个数组A和f,分别为初始棋盘和翻转位置。其中翻转位置共有3个。请返回翻转后的棋盘。 测试样例: [[0,0,1,1],[1,0,1,0],[0,1,1,0],[0,0,1,0]],[[2,2],[3,3],[4,4]] 返回:[[0,1,1,1],[0,0,1,0],[0,1,1,0],[0,0,1,0]] ''' ''' 腾讯2018春招 [编程题] 翻转数列 时间限制:1秒 空间限制:32768K 小Q定义了一种数列称为翻转数列: 给定整数n和m, 满足n能被2m整除。对于一串连续递增整数数列1, 2, 3, 4..., 每隔m个符号翻转一次, 最初符号为'-';。 例如n = 8, m = 2, 数列就是: -1, -2, +3, +4, -5, -6, +7, +8. 而n = 4, m = 1, 数列就是: -1, +2, -3, + 4. 小Q现在希望你能帮他算算前n项和为多少。 输入描述: 输入包括两个整数n和m(2 <= n <= 10^9, 1 <= m), 并且满足n能被2m整除。 输出描述: 输出一个整数, 表示前n项和。 输入例子1: 8 2 输出例子1: 8 # 效率不够,因为10^9,直接数学看出规律即可 n,m=map(int,input().split()) out=0 out=n//(2*m)*(m**2) print (out) ''' ''' [编程题] 纸牌游戏 时间限制:1秒 空间限制:32768K 牛牛和羊羊正在玩一个纸牌游戏。这个游戏一共有n张纸牌, 第i张纸牌上写着数字ai。 牛牛和羊羊轮流抽牌, 牛牛先抽, 每次抽牌他们可以从纸牌堆中任意选择一张抽出, 直到纸牌被抽完。 他们的得分等于他们抽到的纸牌数字总和。 现在假设牛牛和羊羊都采用最优策略, 请你计算出游戏结束后牛牛得分减去羊羊得分等于多少。 输入描述: 输入包括两行。 第一行包括一个正整数n(1 <= n <= 105),表示纸牌的数量。 第二行包括n个正整数ai(1 <= ai <= 109),表示每张纸牌上的数字。 输出描述: 输出一个整数, 表示游戏结束后牛牛得分减去羊羊得分等于多少。 输入例子1: 3 2 7 4 输出例子1: 5 a=int(input()) arr=[int(i)for i in input().split()] arr.sort(reverse=True) first=0 second=0 for i in range(len(arr)): if i%2==0: first+=arr[i] else: second+=arr[i] print(first-second) ''' ''' [编程题] 贪吃的小Q 时间限制:1秒 空间限制:32768K 小Q的父母要出差N天,走之前给小Q留下了M块巧克力。小Q决定每天吃的巧克力数量不少于前一天吃的一半,但是他又不想在父母回来之前的某一天没有巧克力吃,请问他第一天最多能吃多少块巧克力 输入描述: 每个输入包含一个测试用例。 每个测试用例的第一行包含两个正整数,表示父母出差的天数N(N<=50000)和巧克力的数量M(N<=M<=100000)。 输出描述: 输出一个数表示小Q第一天最多能吃多少块巧克力。 输入例子1: 3 7 输出例子1: 4 2分加速的题目 n,m=map(int,input().split()) def panding(a): chi=a for i in range(1,(n)): chi+=(a+1)//2 a=(a+1)//2 return chi<=m first=0 end=m while (end-first>1): mid=(end+first)//2 if panding(mid)==True: first=mid else: end=mid if n==1: print(m) else: if panding(first)==True: print(first) else: print(end) ''' ''' [编程题] 小Q的歌单 时间限制:1秒 空间限制:32768K 小Q有X首长度为A的不同的歌和Y首长度为B的不同的歌,现在小Q想用这些歌组成一个总长度正好为K的歌单,每首歌最多只能在歌单中出现一次,在不考虑歌单内歌曲的先后顺序的情况下,请问有多少种组成歌单的方法。 输入描述: 每个输入包含一个测试用例。 每个测试用例的第一行包含一个整数,表示歌单的总长度K(1<=K<=1000)。 接下来的一行包含四个正整数,分别表示歌的第一种长度A(A<=10)和数量X(X<=100)以及歌的第二种长度B(B<=10)和数量Y(Y<=100)。保证A不等于B。 输出描述: 输出一个整数,表示组成歌单的方法取模。因为答案可能会很大,输出对1000000007取模的结果。 输入例子1: 5 2 3 3 3 输出例子1: 9 def C(n,m): m1 = m m2 = m uper = 1 while(m1>0): uper *= n m1 -= 1 n -= 1 downer = 1 while(m2>0): downer *= m2 m2 -= 1 return int((uper/downer)) K = int(input()) A, X, B, Y = map(int, input().strip().split(' ')) result = 0 for x in range(X+1): for y in range(Y+1): k = A * x + B * y #这题目居然强试出来......,因为是2个物品,所以强试for循环比背包算法要快. if k == K: result += C(X,x) * C(Y,y) result = result % 1000000007 print(result) ''' ''' [编程题] 安排机器 时间限制:1秒 空间限制:32768K 小Q的公司最近接到m个任务, 第i个任务需要xi的时间去完成, 难度等级为yi。 小Q拥有n台机器, 每台机器最长工作时间zi, 机器等级wi。 对于一个任务,它只能交由一台机器来完成, 如果安排给它的机器的最长工作时间小于任务需要的时间, 则不能完成,如果完成这个任务将获得200 * xi + 3 * yi收益。 对于一台机器,它一天只能完成一个任务, 如果它的机器等级小于安排给它的任务难度等级, 则不能完成。 小Q想在今天尽可能的去完成任务, 即完成的任务数量最大。如果有多种安排方案,小Q还想找到收益最大的那个方案。小Q需要你来帮助他计算一下。 输入描述: 输入包括N + M + 1行, 输入的第一行为两个正整数n和m(1 <= n, m <= 100000), 表示机器的数量和任务的数量。 接下来n行,每行两个整数zi和wi(0 < zi < 1000, 0 <= wi <= 100), 表示每台机器的最大工作时间和机器等级。 接下来的m行,每行两个整数xi和yi(0 < xi < 1000, 0 <= yi<= 100), 表示每个任务需要的完成时间和任务的难度等级。 输出描述: 输出两个整数, 分别表示最大能完成的任务数量和获取的收益。 输入例子1: 1 2 100 3 100 2 100 1 输出例子1: 1 20006 ''' ''' [编程题] 构造回文 时间限制:1秒 空间限制:32768K 给定一个字符串s,你可以从中删除一些字符,使得剩下的串是一个回文串。如何删除才能使得回文串最长呢? 输出需要删除的字符个数。 输入描述: 输入数据有多组,每组包含一个字符串s,且保证:1<=s.length<=1000. 输出描述: 对于每组数据,输出一个整数,代表最少需要删除的字符个数。 输入例子1: abcda google 输出例子1: 2 2 看答案: 提到回文串,自然要利用回文串的特点,想到将源字符串逆转后,“回文串”(不一定连续)相当于顺序没变 求原字符串和其反串的最大公共子序列(不是子串,因为可以不连续)的长度(使用动态规划很容易求得),然后用原字符串的长度减去这个最大公共子串的长度就得到了最小编辑长度。 '''