上一篇博客实现了图的基本操作(使用邻接表),包括图的创建、输出、遍历等,这次来实现一下拓扑排序。拓扑排序基本原理可以参考以前转载的一篇博客
http://www.cnblogs.com/zhangbaochong/p/5406159.html
由于代码比较简单,就直接贴出来了
1 #include <queue> 2 #include <vector> 3 #include <stack> 4 #include <iostream> 5 using namespace std; 6 7 8 enum GraphType 9 { 10 UNDIR_UNWEIGHT_GRAPH, //无向无权图 11 UNDIR_WEIGHT_GRAPH, //无向带权图 12 DIR_UNWEIGHT_GRAPH, //有向无权图 13 DIR_WEIGHT_GRAPH //有向带权图 14 }; 15 16 //结点颜色代表遍历情况 17 enum ColorType 18 { 19 WHITE, //未访问 20 GRAY, //正在访问,邻接点还没访问完 21 BLACK //访问完毕 22 }; 23 24 template<typename VertexType, typename InfoType> 25 class Graph 26 { 27 public: 28 Graph(int vertexNum, GraphType type) :m_vertexNum(vertexNum), m_type(type), m_arcNum(0) 29 { 30 for (int i = 0; i < MAX_VERTEX_NUM; ++i) 31 { 32 m_vertices[i].firstArc = nullptr; 33 } 34 } 35 36 void Create() 37 { 38 CreateDirUnweightGraph(); 39 } 40 41 42 //输出图的信息 43 void Display() 44 { 45 for (int i = 0; i < m_vertexNum; ++i) 46 { 47 cout << "第" << i + 1 << "个结点为" << m_vertices[i].data << " 邻接表为:"; 48 ArcNode* node = m_vertices[i].firstArc; 49 while (node) 50 { 51 cout << "->" << m_vertices[node->vertexIndex].data << "(" << node->info << ")"; 52 node = node->next; 53 } 54 cout << endl; 55 } 56 } 57 58 //拓扑排序 59 void TopologicalSort() 60 { 61 cout << "拓扑排序为:"; 62 CountInDegree(); 63 stack<Vertex> s; 64 //把所有入度为0的结点入栈 65 for (int i = 0; i < m_vertexNum; ++i) 66 { 67 if (m_inDegreeArray[i] == 0) 68 s.push(m_vertices[i]); 69 } 70 int count = 0;//输出结点计数,用于判断有没有环 71 while (!s.empty()) 72 { 73 Vertex v = s.top(); 74 s.pop(); 75 cout << v.data << "->"; 76 ++count; 77 ArcNode* node = v.firstArc; 78 while (node) 79 { 80 //从图中删除结点v,v指向的结点入度-1 81 //结点 入度为0加入栈中 82 if (--m_inDegreeArray[node->vertexIndex] == 0) 83 s.push(m_vertices[node->vertexIndex]); 84 node = node->next; 85 } 86 } 87 if (count < m_vertexNum) 88 cout << "图中存在环!" << endl; 89 } 90 private: 91 struct ArcNode 92 { 93 int vertexIndex; //该弧指向的顶点位置 94 struct ArcNode* next; //指向下一个弧 95 InfoType info; //该弧的相关信息,如权重等 96 }; 97 98 struct Vertex 99 { 100 VertexType data; //顶点信息 101 ArcNode* firstArc; //指向第一条依附该节点弧的指针 102 ColorType color; //访问情况 103 }; 104 105 //最大顶点数 106 static const int MAX_VERTEX_NUM = 20; 107 Vertex m_vertices[MAX_VERTEX_NUM]; //顶点列表 108 int m_vertexNum; //当前顶点数量 109 int m_arcNum; //当前弧数量 110 GraphType m_type; //图类型:有向无权图、有向带权图、无向无权图、无向无权图 111 112 //结点入度数组 113 int m_inDegreeArray[MAX_VERTEX_NUM]; 114 private: 115 //初始化顶点列表 116 void InitVertices() 117 { 118 cout << "请输入每个顶点的关键字" << endl; 119 VertexType data; 120 for (int i = 0; i < m_vertexNum; ++i) 121 { 122 cin >> data; 123 m_vertices[i].data = data; 124 } 125 } 126 //插入一个表结点 127 void Insert(int headVertex, int tailVertex, InfoType info) 128 { 129 //构造一个邻接表结点,即创建一条弧 130 ArcNode* newNode = new ArcNode; 131 newNode->info = info; 132 newNode->next = nullptr; 133 newNode->vertexIndex = tailVertex; 134 135 //找到邻接表的最后一个节点 136 ArcNode* lastNode = m_vertices[headVertex].firstArc; 137 if (lastNode == nullptr) 138 m_vertices[headVertex].firstArc = newNode; 139 else 140 { 141 while (lastNode->next) 142 { 143 lastNode = lastNode->next; 144 } 145 lastNode->next = newNode; 146 } 147 ++m_arcNum; 148 } 149 150 //创建有向无权图 151 void CreateDirUnweightGraph() 152 { 153 InitVertices(); 154 cout << "请分别输入每条边的起始结点值:" << endl; 155 int head, tail; 156 while (cin >> head >> tail) 157 { 158 Insert(head, tail, 0); 159 } 160 } 161 162 void CountInDegree() 163 { 164 for (int i = 0; i < m_vertexNum; ++i) 165 { 166 m_inDegreeArray[i] = 0; 167 for (int j = 0; j < m_vertexNum; ++j) 168 { 169 ArcNode* node = m_vertices[j].firstArc; 170 while (node) 171 { 172 if (node->vertexIndex == i) 173 { 174 ++m_inDegreeArray[i]; 175 } 176 node = node->next; 177 } 178 } 179 } 180 } 181 }; 182 183 int main() 184 { 185 Graph<char, int> g(6, DIR_UNWEIGHT_GRAPH); 186 g.Create(); 187 g.Display(); 188 g.TopologicalSort(); 189 }
测试用的有向图:

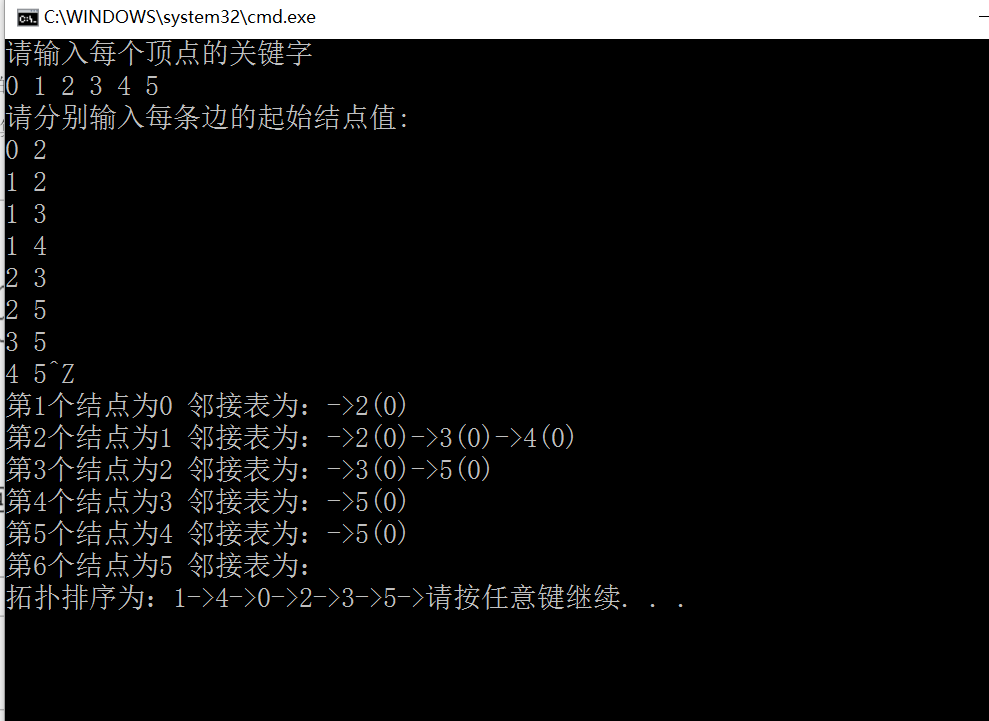
输出结果: