bzoj3529 [Sdoi2014]数表

3529: [Sdoi2014]数表

Time Limit: 10 Sec  Memory Limit: 512 MB
Submit: 2129  Solved: 1064
[Submit][Status][Discuss]

Description

    有一张N×m的数表，其第i行第j列（1 < =i < =n，1 < =j < =m）的数值为
能同时整除i和j的所有自然数之和。给定a，计算数表中不大于a的数之和。

Input

    输入包含多组数据。
    输入的第一行一个整数Q表示测试点内的数据组数，接下来Q行，每行三个整数n，m，a(|a| < =10^9)描述一组数据。

Output

    对每组数据，输出一行一个整数，表示答案模2^31的值。

Sample Input

2
4 4 3
10 10 5

Sample Output

20
148

HINT

1 < =N．m < =10^5  ， 1 < =Q < =2×10^4

Source

Round 1 Day 1

分析：令g(i)表示gcd(x,y) = i的(x,y)的数量，那么利用莫比乌斯反演，很容易可以得到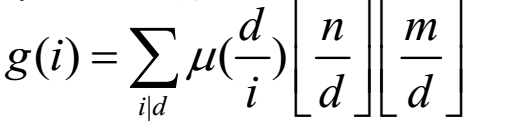，再令F(i)表示i的约数和，n,m范围不大，可以枚举每个数和它的倍数推出来，那么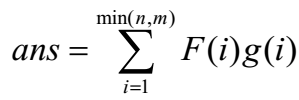，展开一下可以得到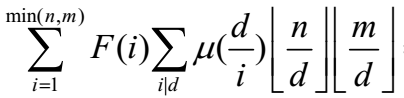：，根据bzoj2820的一些经验，可以把式子变形得到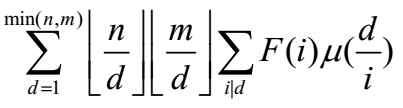：，利用前缀和维护一下就可以做到O(sqrt(n))了.只是题目有限制:F(i) ≤ a.不是很好处理.前缀和肯定是要维护的，只不过现在就要动态维护前缀和了，将a和F(i)从小到大排序.两个指针轮流跳动，每次只将F(i) ≤ a的F(i) * μ(d/i)统计进入前缀和中，为了动态地维护前缀和，可以利用树状数组来解决.

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;

const ll maxn = 100000, mod = 1LL << 31;

ll prime[100010], tot, vis[100010], mo[100010], ans[100010], Q, c[100010], cur1, cur2;

struct node
{
    ll id, x;
}f[100010];

bool cmp(node a, node b)
{
    return a.x < b.x;
}

struct node2
{
    ll n, m, a, id;
}q[20010];

bool cmp2(node2 a, node2 b)
{
    return a.a < b.a;
}

void add(ll x, ll v)
{
    for (ll i = x; i <= maxn; i += i & (-i))
        c[i] += v;
}

ll query(ll x)
{
    ll res = 0;
    while (x)
    {
        res += c[x];
        x -= x & (-x);
    }
    return res;
}

void init()
{
    mo[1] = 1;
    for (ll i = 2; i <= maxn; i++)
    {
        if (!vis[i])
        {
            prime[++tot] = i;
            mo[i] = -1;
        }
        for (ll j = 1; j <= tot; j++)
        {
            ll t = i * prime[j];
            if (t > maxn)
                break;
            vis[t] = 1;
            if (i % prime[j] == 0)
            {
                mo[t] = 0;
                break;
            }
            mo[t] = -mo[i];
        }
    }
    for (ll i = 1; i <= maxn; i++)
    {
        ll x = i;
        for (ll j = x; j <= maxn; j += x)
            f[j].x += x;
        f[i].id = i;
    }
}

ll solve(ll p)
{
    ll res = 0, n = q[p].n, m = q[p].m, last = 0;
    for (ll i = 1; i <= min(n,m); i = last + 1)
    {
        last = min(n / (n / i), m / (m / i));
        res += (n / i) * (m / i) * (query(last) - query(i - 1));
    }
    return res;
}

int main()
{
    init();
    scanf("%lld", &Q);
    for (ll i = 1; i <= Q; i++)
    {
        scanf("%lld%lld%lld", &q[i].n, &q[i].m, &q[i].a);
        q[i].id = i;
    }
    sort(q + 1, q + 1 + Q, cmp2);
    sort(f + 1, f + 1 + maxn, cmp);
    cur1 = cur2 = 1;
    while (cur1 <= Q)
    {
        while (f[cur2].x <= q[cur1].a)
        {
            for (ll i = f[cur2].id; i <= maxn; i += f[cur2].id)
                add(i, f[cur2].x * mo[i / f[cur2].id]);
            cur2++;
        }
        ans[q[cur1].id] = solve(cur1);
        cur1++;
    }
    for (ll i = 1; i <= Q; i++)
        printf("%lld
", ans[i] % mod);

    return 0;
}