轻重链剖分
公元 20XX 年,序列上的数据结构题已经被出题人玩烂了。这些毒瘤们凑在一起,想着如何更新题目的套路。突然,一位毒瘤出题人大开脑洞:“我们为什么不把序列问题搬到树上呢?”
于是树上毒瘤数据结构从此诞生,不过我们也有应对方法——树链剖分。
树链剖分分为三种:轻重链剖分、长链剖分、虚实链剖分(LCT)。
这三种树链剖分本质上都是对树形结构的一种划分方式,不同的是这三者划分方式不同。
今天介绍一种树链剖分的方式——轻重链剖分。
Part 1 Problem
您需要写一个数据结构,要求维护一棵树(点有点权),并支持以下操作:
- 把树上由 (x) 到 (y) 的简单路径上的所有点的点权加上 (z) 。
- 求树上由 (x) 到 (y) 的简单路径上所有点的点权和。
- 把以 (x) 为根节点的子树中所有点的点权加上 (z) 。
- 求以 (x) 为根节点的子树中所有点的点权和。
Part 2 工作原理
轻重链剖分的原理是根据一种特定的深度优先遍历求出一棵树的 dfs 序,根据这个 dfs 序把树“拍平”成一个序列,这样树形结构就变成了线性结构。于是可以使用一些线性数据结构(通常是线段树等)来维护它。
直接介绍工作原理比较难懂,所以先介绍具体做法。大概结合代码来看工作原理会比较好理解吧。
概念
了解具体算法之前,先来看一些概念性的东西:
- 重儿子:对于每个非叶子节点,它的所有儿子中,拥有最大子树的儿子是这个节点的重儿子。
- 轻儿子:对于每个非叶子节点,除了它的重儿子之外,其他的儿子都是轻儿子。
- 叶子节点没有重儿子也没有轻儿子(它压根没儿子。。。
- 重边:一个父节点连接它的重儿子的边称为重边。
- 轻边:非重边。
- 重链:相邻重边组成的一条链称为重链。
- 规定对于叶子节点,如果它是轻儿子,则以它自己为起点有一条长度为 1 的重链。
- 每一条重链的起点是轻儿子。
(所以根应该是轻根)
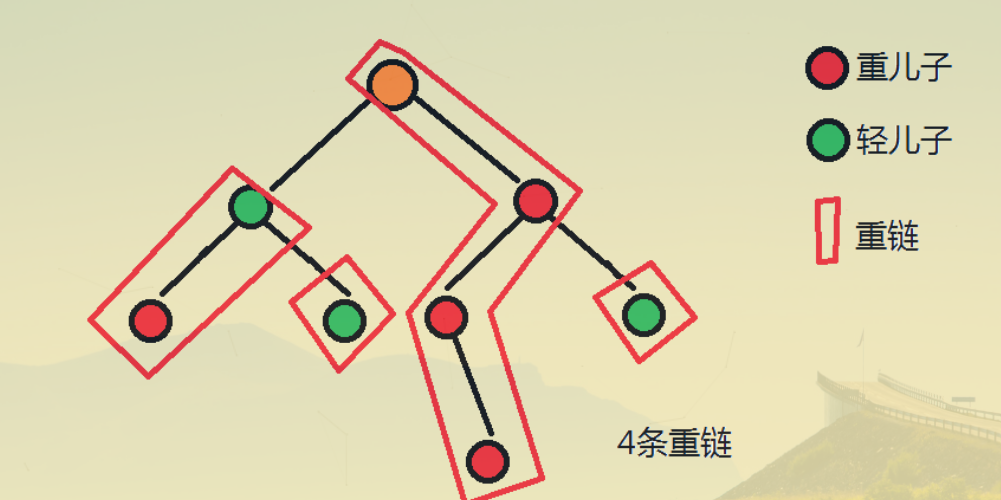
(图片来自 chinhhh 的博客,侵删。)
预处理
树链剖分的预处理有先后两个 dfs 实现,我们暂且叫 dfs1、dfs2 。
dfs1 优先进行,它需要处理每个节点的深度、父亲编号、重儿子编号、子树大小。
代码示例:
int heavy[maxn],dep[maxn],size[maxn],fa[maxn];
//heavy表示重儿子编号、dep为每个节点的深度、size为子树大小、fa为每个节点的父亲编号
void dfs1(const int x,const int f,const int depth){//x为当前节点,f为父亲节点、depth为搜索深度
dep[x]=depth;
fa[x]=f;//记录一下
size[x]=1;//初始化子树大小为1(他自己
int heavysize=-1;//记录最大子树大小
for(int i=0;i<point[x].v.size();++i){//扫描所有出边
int y=point[x].v[i];//出边所达节点
if(y==f) continue;//如果是父亲,跳过
dfs1(y,x,depth+1);//搜索儿子
size[x]+=size[y];//子树大小加上这个儿子的子树大小
if(size[y]>heavysize)//如果这个儿子的子树大小大于已知最大子树大小,更新这个最大值和重儿子编号
heavysize=size[y],heavy[x]=y;
}
}
dfs2 在 dfs1 之后进行,它需要处理每个节点根据轻重链剖分划分出的新编号、新编号下的点权、每个节点所在链的顶端节点。
代码示例:
int top[maxn],newid[maxn],cnt,wt[maxn];
//top为每个点所在链的顶端节点、newid为新编号,cnt
void dfs2(const int x,const int topf){
//x为当前节点,topf表示这个节点的所在链的顶端节点
newid[x]=++cnt;//记录新编号
wt[cnt]=point[x].value;//新编号意义下的点权值
top[x]=topf;//记录顶端节点是谁
if(!heavy[x]) return;//是叶子节点就不用递归了
dfs2(heavy[x],topf);//先递归重儿子(至于为什么,后面会解释)
for(int i=0;i<point[x].v.size();++i){
int y=point[x].v[i];
if(y==fa[x] || y==heavy[x]) continue;//是父亲或者重儿子就跳过
dfs2(y,y);//根据定义,每个轻儿子都有以它自己为顶端节点的重链
}
}
解决问题&&工作原理
为什么要处理新编号,并且优先处理重儿子的编号呢 ?答案来了。
如果我们对上面那棵树进行上面的两个 dfs 过程,会得到下面这样一颗树。
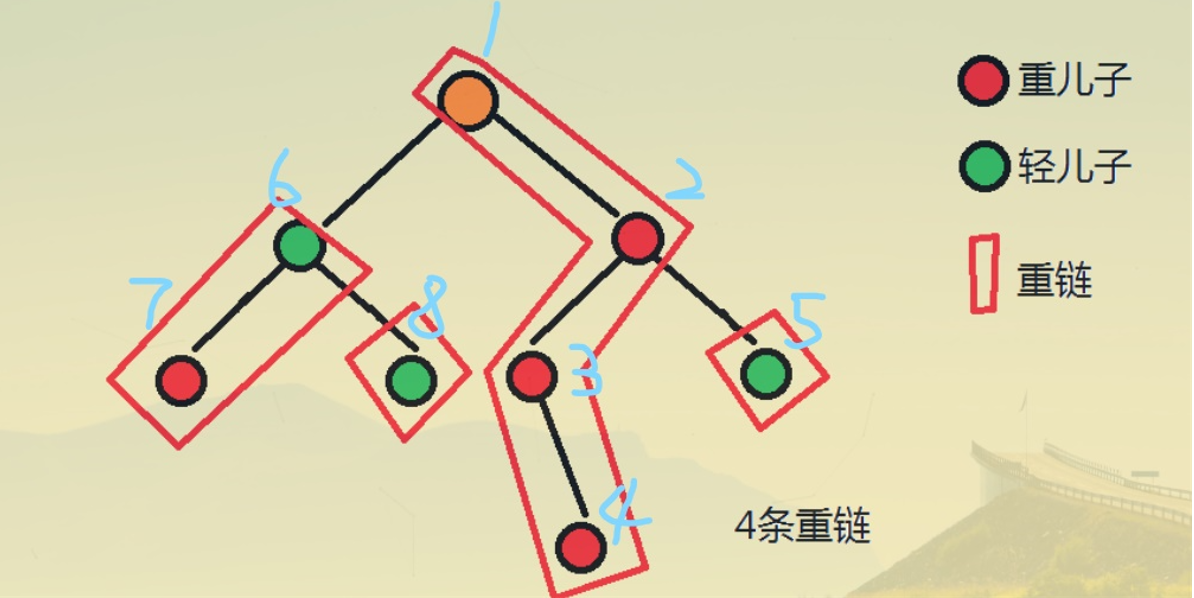
这样优先处理重儿子、重新分配编号的方法使得这颗新树有如下两个优秀性质:
- 因为优先处理重儿子,所以这些重儿子构成的每一条重链,其新编号都是连续的。
- 由于 dfs 的性质,对于每一个节点,其子树内所有节点的编号也是连续的。
因为新编号具有如上的优秀性质(实质上我们已经把这颗树“拍平”了),考虑对新编号建立线段树。
-
对 (x) 的子树求和(修改)
因为子树内节点编号连续,也就是说,新编号意义下,一个节点 (x) 向后 size[x] 个节点都在它的子树内,于是线段树区间求和(区间修改)就行了,复杂度 (O(logn)) 。
-
路径加、路径求和
-
操作流程
两个节点的路径上节点编号不一定连续,所以我们不能直接进行加减。注意到如果两个节点在同一个重链内,节点编号是连续的,这启发我们把两个节点“跳”到同一条链上,一旦两个点在同一条链上,我们就可以直接利用线段树进行区间求和(区间修改)了。
考虑每一次跳一整个链,利用 dfs2 中预处理出来的 top[x] ,求出 (x) 所在链顶端节点编号,这时 top[x] 到 (x) 的节点编号一定是连续的(在一条重链内)。利用线段树区间求和(修改)先统计这一部分的答案,然后把 (x) 调整到 top[x] 的父亲的位置,这时 (x) 一定属于另一条重链,于是可以重复这个“向上跳”的操作。
我们每次把 (x,y) 两个节点中更深的节点“向上跳”,同时统计答案(修改),直到两个节点处于同一条链内,这时两点之间编号连续,直接进行求和(修改)即可。
-
时间复杂度
路径加减、求和应该是 (O(log^2n)) 的,具体我不会证明。如果我之后了解了,会来补上证明。
-
Part 3 完整代码供参考
这段代码实现了洛谷P3384 轻重链剖分一题中的要求。
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<iomanip>
#include<cstring>
#include<utility>
#include<cstdio>
#include<queue>
#include<stack>
#include<ctime>
#include<cmath>
#include<list>
#include<set>
#include<map>
namespace zhang_tao{
const int inf=0x7f7f7f7f;
template <typename _T>
inline _T const& read(_T &x){
x=0;int fh=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')
fh=-1;
ch=getchar();
}
while(isdigit(ch)){
x=x*10+ch-'0';
ch=getchar();
}
return x*=fh;
}
void write(int x){
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+48);
}
inline int _gcd(const int x,const int y){
return y?_gcd(y,x%y):x;
}
inline int _lcm(const int x,const int y){
return x*y/_gcd(x,y);
}
inline int max(int a,int b,int c=-inf){
return std::max(std::max(a,b),c);
}
inline int min(int a,int b,int c=inf){
return std::min(std::min(a,b),c);
}
inline void swap(int &x,int &y){
x^=y^=x^=y;
}
} // namespace zhang_tao
#define ll long long
using namespace zhang_tao;
const int maxn=100005;
int n,m,rot,P;
struct Node{
int value;
std::vector<int>v;
};//存点权和每个点的出边
struct Node point[maxn];
int heavy[maxn],id[maxn],fa[maxn],cnt,dep[maxn],size[maxn],top[maxn],wt[maxn];
//意义同Part 2中提到的
struct segment_tree{
int l,r,value,tag;//l,r表示这个结点代表的区间是[l,r],value表示区间和,tag是懒标记
segment_tree *ls,*rs;
};//线段树
struct segment_tree *root;
inline bool in_range(segment_tree *node,const int L,const int R){
return L<=node->l && node->r<=R;
}//判断一个线段树的结点是否在指定区间内
inline bool outof_range(segment_tree *node,const int L,const int R){
return node->r<L || R<node->l;
}//判断一个线段树的结点是否与指定区间不交
inline void update(segment_tree *node){
node->value=((node->ls->value % P) + (node->rs->value % P))%P;
}//更新线段树的结点
inline void make_tag(segment_tree *node,const ll w){
ll delta=(node->r-node->l+1)*w;
node->value=((node->value%P)+(delta%P))%P;
node->tag+=w;
}//打标记,用于区间修改
inline void push_down(segment_tree *node){
if(node->tag){
make_tag(node->ls,node->tag);
make_tag(node->rs,node->tag);
node->tag=0;
}
}//下传标记
segment_tree *Build(const int L,const int R){
segment_tree *u=new segment_tree;
u->l=L,u->r=R;
u->tag=0;
if(L==R){
u->value=(wt[L]%P);
u->ls=u->rs=NULL;
}else{
int Mid=(L+R)>>1;
u->ls=Build(L,Mid);
u->rs=Build(Mid+1,R);
update(u);
}
return u;
}//建树
int query(segment_tree *node,const int L,const int R){
if(in_range(node,L,R)) return node->value%P;//完全在区间内,返回这个结点的值
if(outof_range(node,L,R)) return 0;//与区间不交,返回0
push_down(node);
return ((query(node->ls,L,R)%P) + (query(node->rs,L,R)%P)) %P;//向左右子树递归查询
}//查询
void modify(segment_tree *node,const int L,const int R,const int w){
if(in_range(node,L,R)){
make_tag(node,w);//完全在区间内,打上标记
return;
}else if(!outof_range(node,L,R)){
push_down(node);//与区间有交,那么向左右子树递归
modify(node->ls,L,R,w);
modify(node->rs,L,R,w);
update(node);
}
}
int sum_path(int x,int y){
int ans=0;
while(top[x]!=top[y]){//当x,y不在一条重链上时
if(dep[top[x]]<dep[top[y]]) swap(x,y);
ans+=query(root,id[top[x]],id[x]);//查询深度较深的那个重链的和
ans%=P;
x=fa[top[x]];//跳到这个重链的顶端结点的父亲,即为下一条重链
}
if(dep[x]>dep[y]) swap(x,y);
ans+=query(root,id[x],id[y]);//在一个链上就直接查询x到y的和
ans%=P;
return ans;
}
void modify_path(int x,int y,int w){
w%=P;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
modify(root,id[top[x]],id[x],w);
x=fa[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
modify(root,id[x],id[y],w);
}//原理同路径查询
int sum_sontree(const int x){
return query(root,id[x],id[x]+size[x]-1);
}//一个子树的dfs序连续,最后一个结点是id[x]+size[x]-1
void modify_sontree(const int x,int w){
w%=P;
modify(root,id[x],id[x]+size[x]-1,w);
}//原理同子树查询
void dfs1(const int x,const int f,const int deep){
dep[x]=deep;
fa[x]=f;
size[x]=1;
int heavysize=-1;
for(int i=0;i<point[x].v.size();++i){
int y=point[x].v[i];
if(y==f) continue;
dfs1(y,x,deep+1);
size[x]+=size[y];
if(size[y]>heavysize)
heavysize=size[y],heavy[x]=y;
}
}//意义同Part 2中提到的
void dfs2(const int x,const int topf){
id[x]=++cnt;
wt[cnt]=point[x].value;
top[x]=topf;
if(!heavy[x]) return;
dfs2(heavy[x],topf);
for(int i=0;i<point[x].v.size();++i){
int y=point[x].v[i];
if(y==fa[x] || y==heavy[x]) continue;
dfs2(y,y);
}
}//意义同Part 2中提到的
signed main(){
read(n),read(m),read(rot),read(P);
for(int i=1;i<=n;++i)
read(point[i].value);
for(int i=1,x,y;i<=n-1;++i){
read(x),read(y);
point[x].v.push_back(y);
point[y].v.push_back(x);
}
dfs1(rot,0,1);
dfs2(rot,rot);
root=Build(1,cnt);//预处理
while(m--){//回答问题、修改点权
int k,x,y,z;
read(k);
switch(k){
case 1 :
read(x),read(y),read(z);
modify_path(x,y,z);
break;
case 2 :
read(x),read(y);
write(sum_path(x,y)),putchar('
');
break;
case 3 :
read(x),read(y);
modify_sontree(x,y);
break;
case 4 :
read(x);
write(sum_sontree(x)),putchar('
');
break;
default :
break;
}
}
return 0;
}