01玩转数据结构_08_堆和优先队列

堆：

树这种结构本身在计算机科学领域占有很重要的地位，这种数据结构之所以占有重要的地位，不仅仅是因为二分搜索树这样的一种结构，是树本身这种形状可以产生很多拓展，对于不同的问题，我们可以稍微改变或者限制树这种数据结构的性质，从而产生不同的数据结构，高效的解决不同的问题，

从节开始，将会有四个章节介绍四个不同的例子，它们分别是堆，线段树，字典树以及并查集 ，通过这些不同的树的结构，我们可以领会到数据结构的灵活之处，

什么是优先队列：

优先队列（相对高层的数据结构）是出队，入队和顺序无关，和 优先级 有关，其实用的最多是谁优先出队，

优先队列的接口和普通队列是一样，只不过是在出队操作上和队首元素上是不同的，

优先队列的底层结构实现也是可以由不同数据结构来构成，这里提供的是三种类型的数据结（普通线性结构，顺序线性结构，堆）

这里假设优先级是谁最大，

这里是用堆作为数据结构作为优先队列的底层实现，如果有时间也可以用普通线性结构或者顺序线性结构来实现优先队列然后再和我们这里用堆实现的优先队列去比较性能，这有助于对数据结果的学习！

堆的基本结构：

在计算机的世界中，凡是时间复杂度为 logn 的，那么差不多一定和树这个结构有关系，归并排序和快速排序它们都是logn 级别的，（虽然没有直接使用树，但是它的递归过程其实是个隐形树）

一个堆本身，其实也是一颗树，

二叉堆：

二叉堆是一个特殊的树，二叉堆是一课完全二叉树，

满二叉树：除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。

完全二叉树：完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

满二叉树：

完全二叉树：（其实就是一层一层的放，直到放不下了）

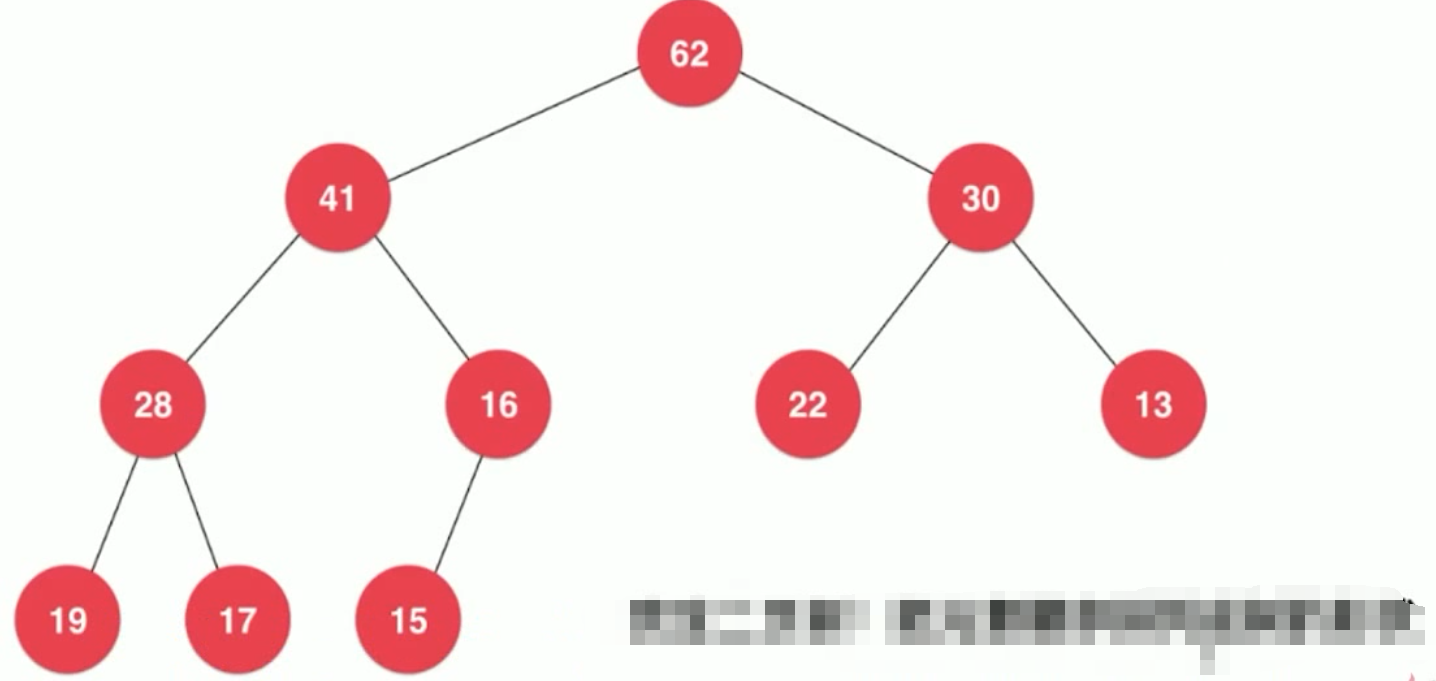
二叉堆首先是个完全二叉树，除此之外，

它还有个特殊的性质：堆中每个节点的值总是不大于其父节点的值（所有个节点值都大于它的孩子的值 ）。这个时候的堆，我们叫做最大堆（每个节点值都大于它的孩子的节点的值），相应也可以定义出最小堆！

总结：最大堆：首先是个完全二叉树，然后，每个节点的值都大于它的孩子节点的值！

实现堆的底层结构：

当然可以使用二叉搜索树（使用Node ，left ,right），但是，因为堆是一层一层的，我们可以使用数组来实现堆，

此时，如何寻找一个节点的左右孩子呢？

其实是有规律的：

一个节点的左孩子的索引 = 该节点 索引 * 2

一个节点的右孩子的索引 = 该节点 索引 * 2 + 1

而且：对于一个节点，它的父节点的索引= 该节点的 索引 / 2 （注：这里是整除，）

注：上图中根节点，我们都是从 1 开始标，这样有助于计算，但是，此时的数组中索引 0 就空出来了，不过从0 开始也可，只不过索引关系会发生一点改变而已，

下面实现MaxHeap 最大堆：

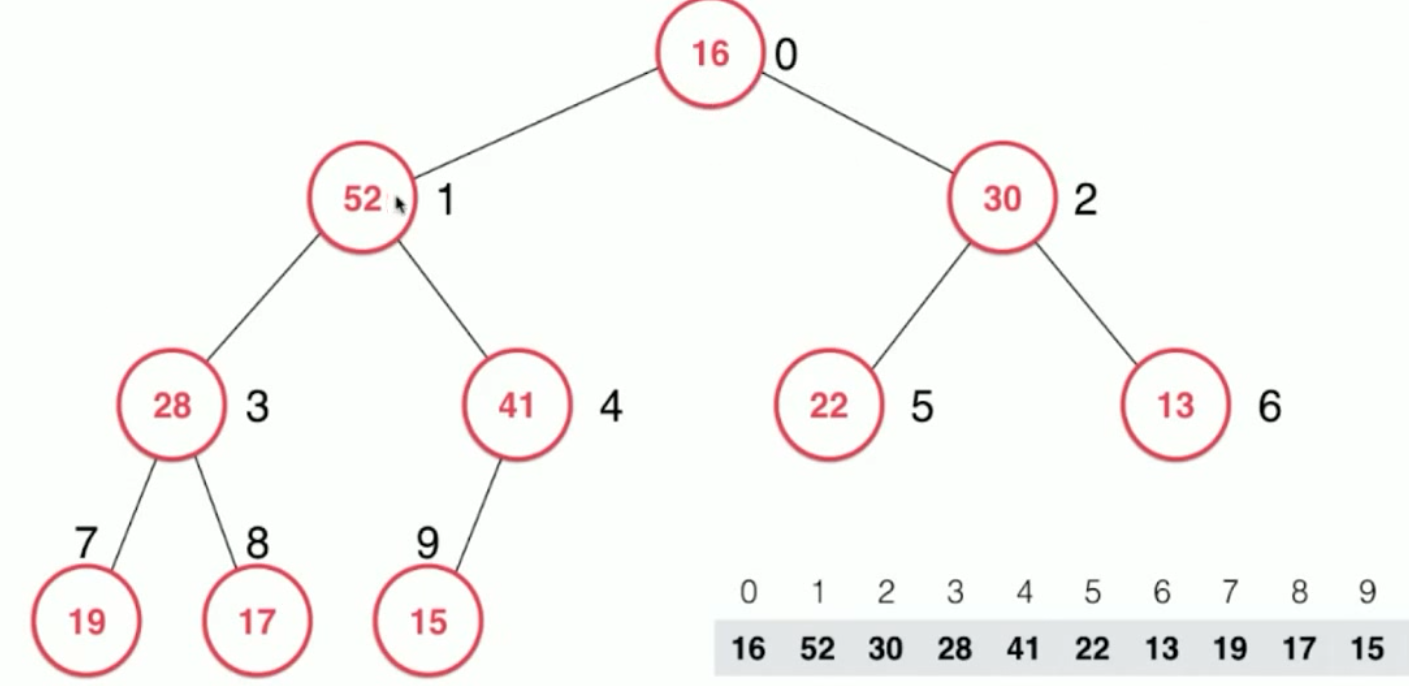
向堆中添加元素(sift up )时：

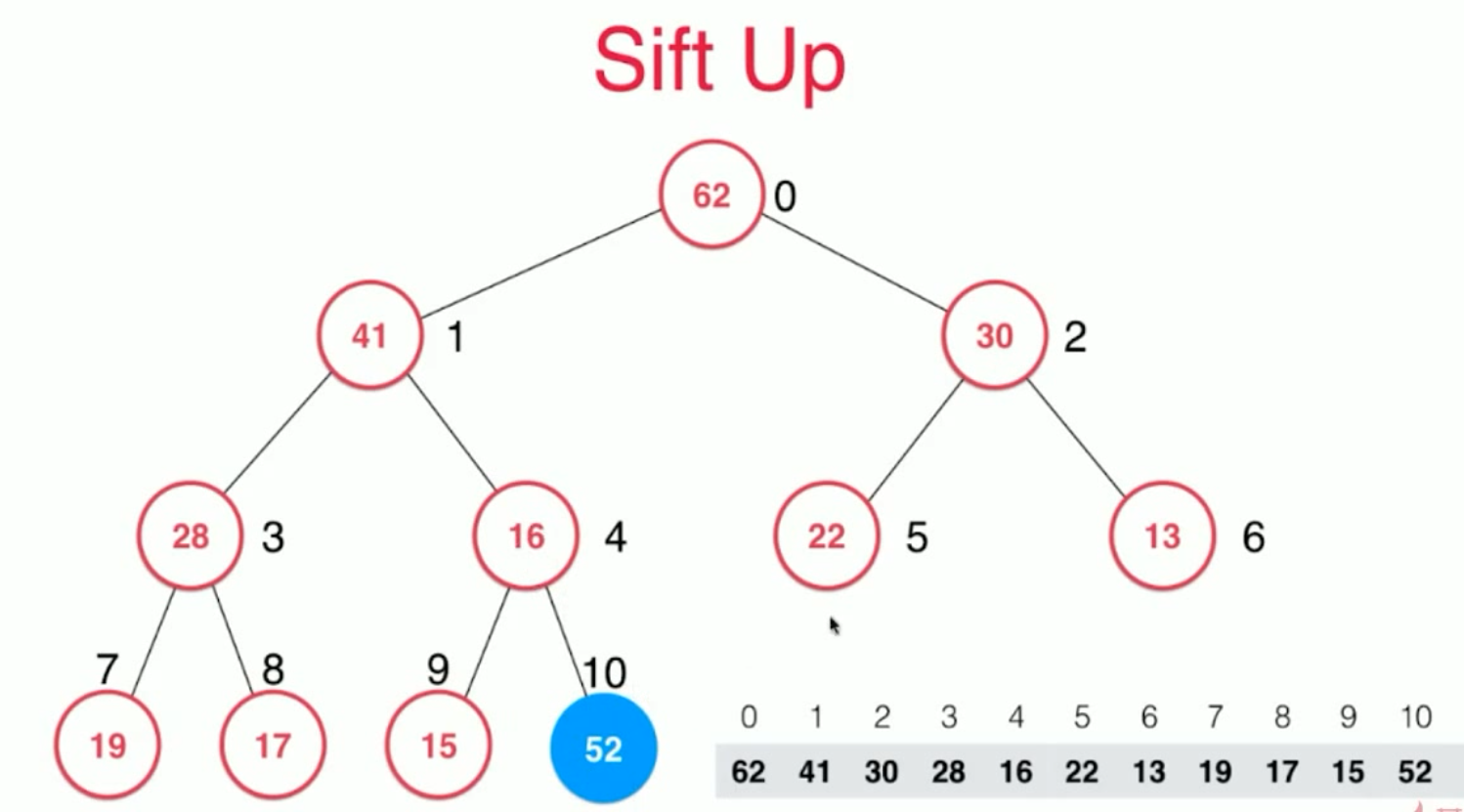
单单加进来，还不行，因为16 已经不大于 52了，所以此时还要进行调整，

调整方案就是从添加的元素位置一路向上找父亲节点进行比较，大的上浮，

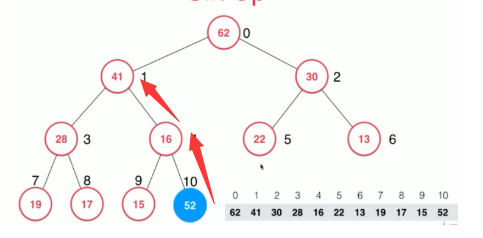
调整之后的方案：

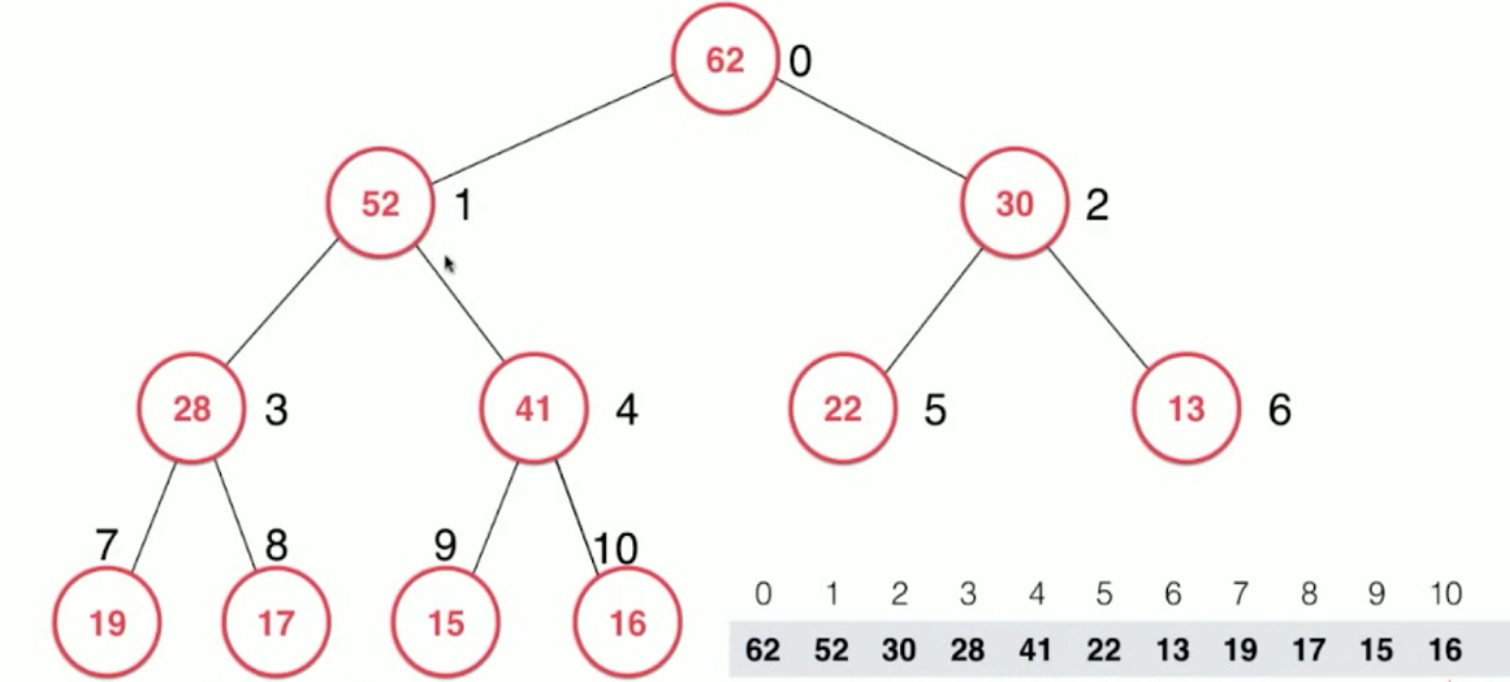
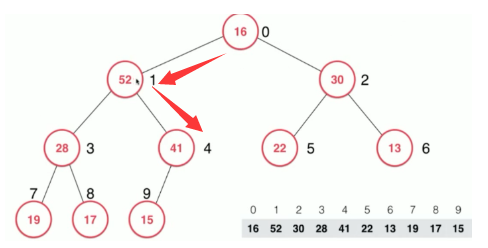
向堆中取出元素(sift down )时：

此时，将堆顶元素直接去掉，然后，还是将最后一层最后一个放过去，

但是，此时是不满足最大堆的最大性质的，所以还是需要进行调整，

这时候需要将 16 下沉下来，每次它和两个孩子大小进行比较，选择较大的，（如果它比自己还大）进行下沉交换。

即：

  1 package zcb.demo03;
  2 
  3 public class MyArray<T> {
  4     private T[] data; //数组
  5     private int size;  //数组实际大小，
  6     //容量不用写，可以由data.length()得知
  7 
  8     //满参构造函数
  9     public MyArray(int capacity){
 10 //        this.data  = new int[capacity];
 11 //        this.data  = new T[capacity];  //不支持这样
 12         this.data =  (T[]) new Object[capacity];  //先new 出个 Object[]  类的，然后转为 T[]
 13         this.size = 0; //开始时 实际大小size =0
 14     }
 15     //空参构造器
 16     public MyArray(){
 17         this(10);  //如果是空参的话，调用有参构造器。默认是10
 18     }
 19 
 20     //获取数组中的元素的个数
 21     public int getSize(){
 22         return this.size;
 23     }
 24 
 25     //获取数组的容量
 26     public int getCapacity(){
 27         return this.data.length;
 28     }
 29 
 30     //数组中是否为空
 31     public boolean isEmpty(){
 32         return this.size ==0;
 33     }
 34     /////////////////////增////////////////////////////
 35     //向 数组的末尾添加一个新元素
 36     public void addLast(T num){
 37         /*
 38         if(size == this.data.length){
 39             //此时开辟的空间已经满了
 40             //这里先抛出一个异常
 41             throw new IllegalArgumentException("addLast failed.数组已经满了");
 42         }
 43         this.data[size] = num;
 44         size ++;  //要维持数组  指针。 size 是当前数组中的个数。
 45         */
 46         //此时其实可以直接复用 insert ()函数
 47         insert(this.size,num);
 48     }
 49     // 向数组头添加元素 （直接复用  向指定位置添加元素的函数 ）
 50     public void addFirst(T num){
 51         insert(0,num);
 52     }
 53 
 54     //向 指定数组位置添加一个新元素
 55     public void insert(int idx,T num){
 56         if(this.size == this.data.length){
 57 //            throw new IllegalArgumentException("数组已经放满了");
 58             /*此时对其扩容*/
 59             resize(2*this.data.length);
 60 
 61 
 62         }
 63         if(idx <0 || idx > this.size )
 64             throw new IllegalArgumentException("索引非法");
 65 
 66         for(int i=this.size-1;i >= idx;--i){
 67             this.data[i+1] = this.data[i];
 68         }
 69         this.data[idx] = num;
 70         //更新size
 71         this.size ++;
 72     }
 73 
 74     //////////////////////删///////////////////////////////////////
 75     //删除第一个
 76     public T removeFirst(){
 77         return remove(0);  //删除并将之返回出去
 78     }
 79 
 80     //删除最后一个
 81     public T removeLast(){
 82         return remove(this.size-1);
 83     }
 84 
 85     //删除指定位置  的元素
 86     public T remove(int idx){  //返回 删除的元素
 87         if(idx < 0 || idx > this.size -1)
 88             throw new IllegalArgumentException("idx错误！");
 89         T temp = this.data[idx];
 90         for (int i =idx;i<this.size - 1;i++){
 91             this.data[i] = this.data[i+1];
 92         }
 93         this.size -- ;
 94 
 95         //动态减少   当数组中的元素少于空间的一半的时候，就缩减空间。
 96         if(this.size == this.data.length / 2){
 97             System.out.println("size = "+this.size);
 98 
 99             resize(this.data.length/2);
100         }
101         return temp;
102     }
103 
104     //删除 某个元素 不根据其位置  //它之所以返回void 是因为调用着已经知道的element ，所以没必要再返回出来了。
105     public void removeElement(T element){
106         //首先要 寻找是否有 element
107         int idx = find(element);
108         if(idx == -1){
109             throw new IllegalArgumentException("没有该元素");
110         }else{
111             remove(idx);
112         }
113     }
114 
115     //////////////////////改///////////////////////////////////////
116     //修改索引为 idx 的元素为 num
117     public void setByIndex(int idx,T num){
118         if(idx <0 || idx > this.size)
119             throw new IllegalArgumentException("idx 错误！");
120 
121         this.data[idx] = num;
122     }
123 
124 
125     //////////////////////查///////////////////////////////////////
126     //获取整个数组的概括
127     //重写 toString()  当打印arr 时候，就会调用该方法！
128     @Override
129     public String toString(){
130         StringBuilder res = new StringBuilder();
131         res.append(String.format("Array:size = %d,capacity = %d 
",this.size,this.data.length));
132         res.append('[');
133         for (int i =0 ;i<this.size;i++){
134             res.append(data[i]);
135             if(i != this.size -1)
136                 res.append(", ");
137         }
138         res.append(']');
139         return res.toString();
140     }
141     //获取idx 索引位置的 元素
142     public T getByIndex(int idx){
143         if (idx < 0 || idx >this.size) {
144             throw new IllegalArgumentException("索引传入错误！");
145         }
146         return this.data[idx];
147     }
148 
149     //////////////////////包含///////////////////////////////////////
150     public boolean contains(T num){
151         for (int i=0;i<this.size;i++){
152             if(this.data[i] == num){
153                 return true;
154             }
155         }
156         return false;
157     }
158     //////////////////////寻找////////////////////////////////////
159     public int find(T num){
160         //寻找数组中是否有 num  ,如果有返回其索引，反之 返回-1
161         for (int i =0;i<this.size;i++){
162             if(this.data[i] == num){
163                 return i;
164             }
165         }
166         return -1;
167     }
168     //////////////////////实现动态数组  resize()////////////////////////////////////
169     private void resize(int new_capacity){  //之所以  用 private 是不让用户调用， 数组如果空间不足会自己扩展的。
170         T[] new_data =(T[]) new Object[new_capacity];
171 
172         for (int i =0;i<this.size;i++){
173             new_data[i] = this.data[i];
174         }
175         //
176         this.data = new_data;  //此时新数组的size 不变 ， 新数组的length 也不用变
177     }
178 }

MyArray.java

  1 package zcb.demo03;
  2 
  3 public class MaxHeap<T extends Comparable<T>> {
  4     private MyArray<T> arr;
  5 
  6     // 构造函数
  7     public MaxHeap(int capacity){
  8         // 已知容量
  9         arr = new MyArray<>(capacity);
 10     }
 11     public MaxHeap(){
 12         arr = new MyArray<>();
 13     }
 14 
 15     // 返回堆中的 元素个数
 16     public int getSize(){
 17         return arr.getSize();
 18     }
 19     // 堆中是否为空
 20     public boolean isEmpty(){
 21         return arr.isEmpty();
 22     }
 23     // 下面是三个 私有的辅助函数
 24     // 根据当前节点的索引 算出左孩子的索引 (数组从0 就存值)
 25     private int getIdx_left(int cur_idx){
 26 
 27         return (cur_idx + 1)*2;
 28     }
 29     // 根据当前节点的索引 算出右孩子的索引
 30     private int getIdx_right(int cur_idx){
 31 
 32         return (cur_idx + 1)*2 - 1;
 33     }
 34     // 根据当前节点的索引 算出父亲节点的索引
 35     private int getIdx_par(int cur_idx){
 36         if(cur_idx == 0){
 37             throw new IllegalArgumentException("根节点 没有父亲节点");
 38         }
 39         return (cur_idx - 1) /2;
 40     }
 41 
 42     // 向堆中添加 元素
 43     public void add(T t){
 44         arr.addLast(t);
 45         if(arr.getSize() == 1){
 46             // 不需要调整位置了
 47             return ;
 48         }
 49         // 调整位置 siftUp()
 50         siftUp(arr.getSize() - 1);
 51     }
 52     private void siftUp(int cur_idx){
 53         int par_idx = getIdx_par(cur_idx);
 54 
 55         while ( arr.getByIndex(cur_idx).compareTo( arr.getByIndex(par_idx) ) > 0 ){
 56             // 上浮
 57             T temp = arr.getByIndex(cur_idx);
 58             arr.setByIndex(cur_idx,arr.getByIndex(par_idx));
 59             arr.setByIndex(par_idx,temp);
 60 
 61             cur_idx = par_idx;
 62             if(cur_idx == 0)
 63                 break;
 64             par_idx = getIdx_par(cur_idx);
 65         }
 66     }
 67 
 68     // 从堆中 取出元素  （取出元素的时候，我们只取出 堆顶元素（最大的））
 69     public T removeMax(){
 70         if(arr.isEmpty()){
 71             return null;
 72         }
 73         T ret = arr.getByIndex(0);
 74         arr.setByIndex(0,arr.getByIndex(arr.getSize() - 1));
 75         arr.remove(arr.getSize() - 1);
 76 
 77         if(arr.getSize() == 1){
 78             // 此时不需要调整
 79             return arr.getByIndex(0);
 80         }
 81 
 82         //进行 下沉调整 操作
 83         siftDown(0);
 84         return ret;
 85     }
 86     private void siftDown(int par_idx){        // 也可以不使用 递归 ！！！（使用循环   ）
 87         int left_idx = getIdx_left(par_idx);
 88         int right_idx = getIdx_right(par_idx);
 89         if(left_idx > arr.getSize() -1 || right_idx > arr.getSize() -1){
 90             return;
 91         }
 92         if(arr.getByIndex(par_idx).compareTo(arr.getByIndex(left_idx)) > 0 && arr.getByIndex(par_idx).compareTo(arr.getByIndex(left_idx)) >0 ){
 93             return;
 94         }
 95         if(arr.getByIndex(left_idx).compareTo(arr.getByIndex(right_idx))> 0){
 96            // 向左 交换
 97             T temp = arr.getByIndex(par_idx );
 98             arr.setByIndex(par_idx,arr.getByIndex(left_idx));
 99             arr.setByIndex(left_idx,temp);
100             siftDown(left_idx);
101         }else{
102             // 向右 交换
103             T temp = arr.getByIndex(par_idx );
104             arr.setByIndex(par_idx,arr.getByIndex(right_idx));
105             arr.setByIndex(right_idx,temp);
106             siftDown(right_idx);
107         }
108     }
109 
110 
111 
112 
113 
114 
115 
116     @Override
117     public String toString() {
118         return arr.toString();
119     }
120 }

MaxHeap.java

 1 package zcb.demo03;
 2 
 3 public class test {
 4     public static void main(String[] args) {
 5         MaxHeap<Integer> heap = new MaxHeap<>();
 6 
 7         heap.add(62);
 8         heap.add(52);
 9         heap.add(30);
10         heap.add(28);
11         heap.add(41);
12         heap.add(22);
13         heap.add(13);
14         heap.add(19);
15         heap.add(17);
16         heap.add(15);
17         heap.add(16);
18 
19         System.out.println(heap);
20         
21         int ret1 = heap.removeMax();
22         System.out.println(ret1);
23         System.out.println(heap);
24 
25         int ret2 =  heap.removeMax();
26         System.out.println(ret2);
27         System.out.println(heap);
28 
29 
30     }
31 
32 }

test.java

我们也可以发现，最大堆对应的数组就是从大到小的排序，这就是所谓的堆排序算法的基本思想，

堆的时间复杂度：

它还是二叉树的高度，添加和删除都是 O logn 级别的，

特殊之处是因为堆是个完全二叉树，所以它的最差情况也是 O logn ,

堆上的另外两个操作 replace 和 heapify：

1， replace:

我们可以通过先 removeMax() 之后，然后再 add() 一个新元素，时间复杂度为两次 log n 。

其实，可以直接将堆顶元素替换以后，然后 siftDown ,这样的时间复杂度为一次 log n 。

2 ,heapify

将任意一个数组整理成堆的形状，

现在任意来了一个数组，只要是我们合理的交换数组中的位置，它也可以是个堆的形状，

直观的想法是扫描一下整个数组，把它添加到我们实现的堆里面就可以了，

不过这有个更快的做法：

我们假设整个任意数组看做是个完全二叉树，

如下：

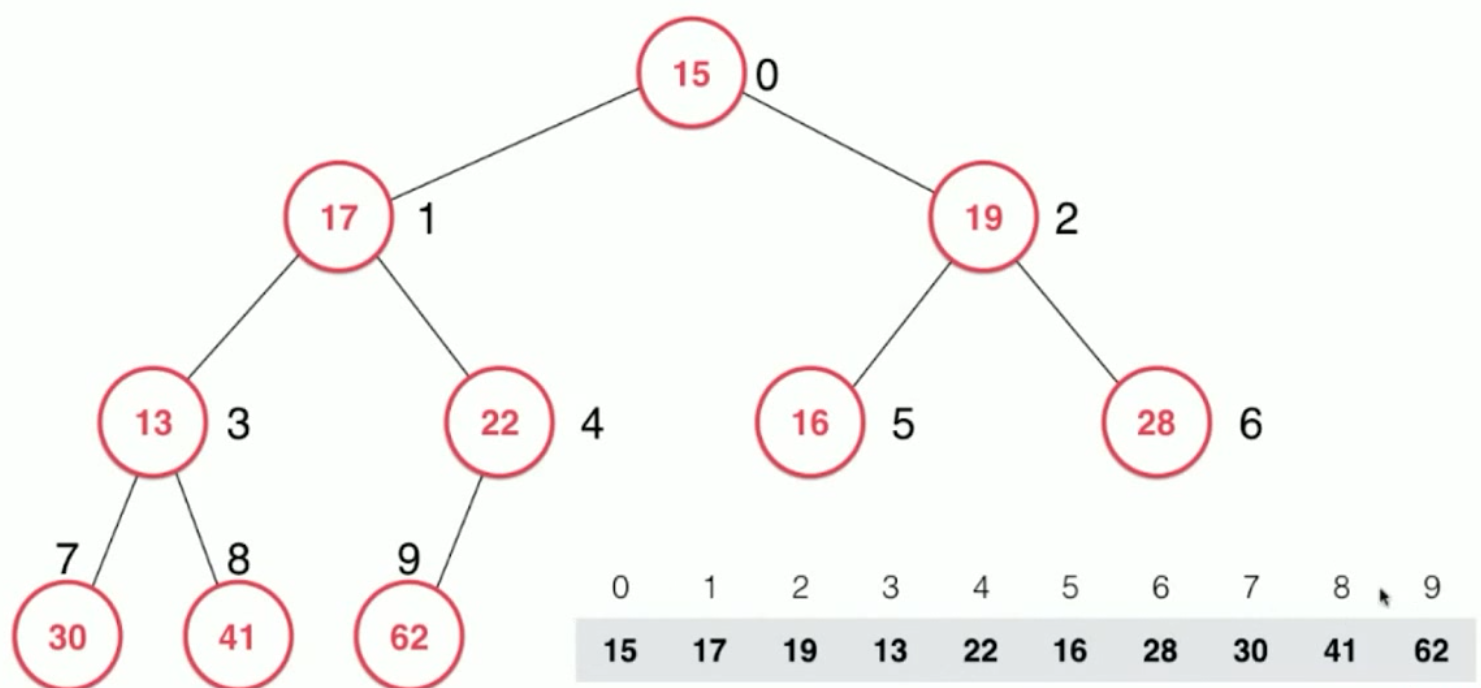
然后，从倒数第一个非叶子结点开始（每个非叶子结点都要走一遍），即上面的 22 结点，不断的进行 siftDown（记得每次都要下沉到底）操作即可，

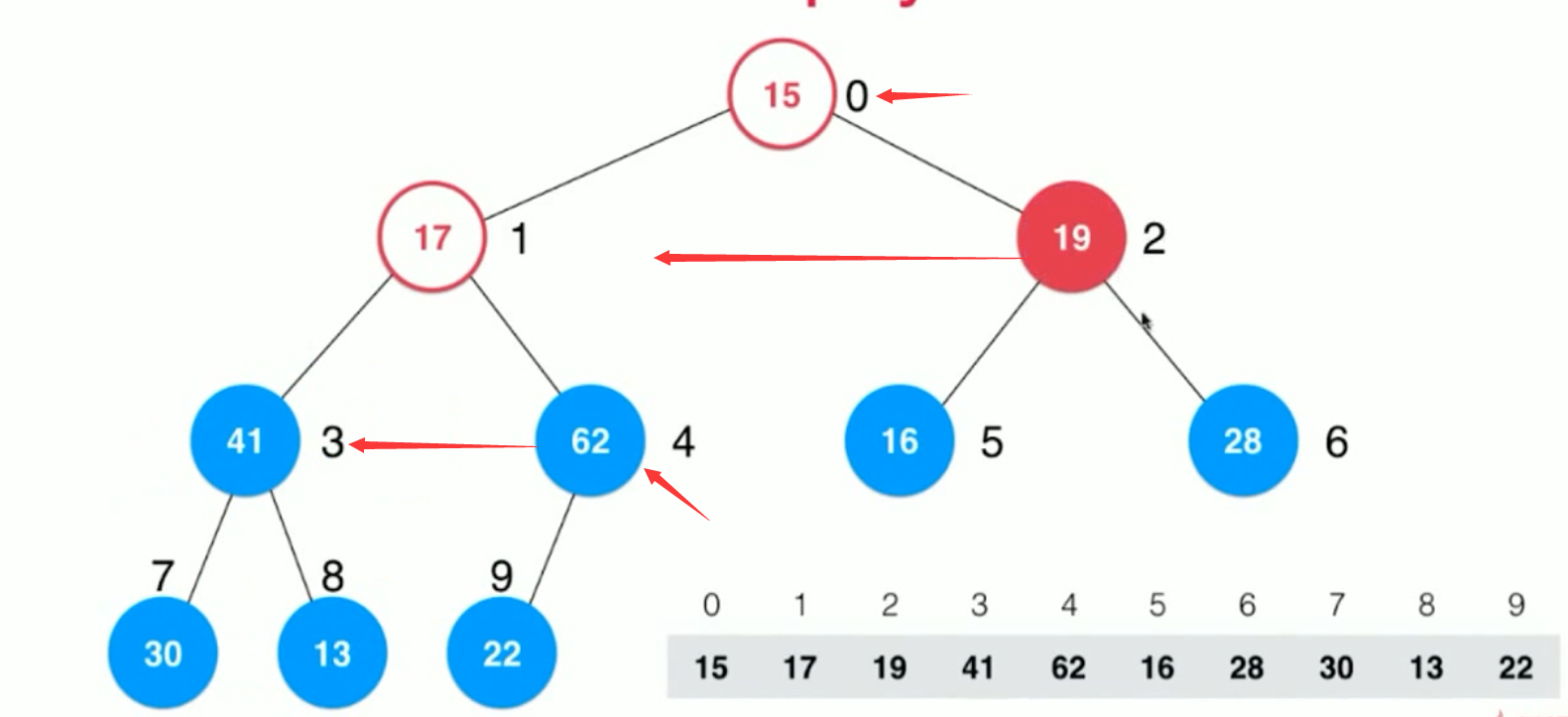
最终为：

这里的关键点是：

1，如何定位到倒数第一个非叶子结点所处的索引是多少？

其实很简单，只需要拿到最后一个索引，然后依据它计算它的父亲的索引即可，

这样之所以快是，我们一上来就抛弃了所有的叶子结点，（很多的哦），这比一个一个添加要快

实际上，将n 个元素插入到一个空堆中，算法的时间复杂度是：O（n logn ）

但是，上面的方法算法时间复杂度是 O (n ) , 具体如何算出不谈，

  1 package zcb.demo03;
  2 
  3 public class MyArray<T> {
  4     private T[] data; //数组
  5     private int size;  //数组实际大小，
  6     //容量不用写，可以由data.length()得知
  7 
  8     //满参构造函数
  9     public MyArray(int capacity){
 10 //        this.data  = new int[capacity];
 11 //        this.data  = new T[capacity];  //不支持这样
 12         this.data =  (T[]) new Object[capacity];  //先new 出个 Object[]  类的，然后转为 T[]
 13         this.size = 0; //开始时 实际大小size =0
 14     }
 15     //空参构造器
 16     public MyArray(){
 17         this(10);  //如果是空参的话，调用有参构造器。默认是10
 18     }
 19 
 20     //获取数组中的元素的个数
 21     public int getSize(){
 22         return this.size;
 23     }
 24 
 25     //获取数组的容量
 26     public int getCapacity(){
 27         return this.data.length;
 28     }
 29 
 30     //数组中是否为空
 31     public boolean isEmpty(){
 32         return this.size ==0;
 33     }
 34     /////////////////////增////////////////////////////
 35     //向 数组的末尾添加一个新元素
 36     public void addLast(T num){
 37         /*
 38         if(size == this.data.length){
 39             //此时开辟的空间已经满了
 40             //这里先抛出一个异常
 41             throw new IllegalArgumentException("addLast failed.数组已经满了");
 42         }
 43         this.data[size] = num;
 44         size ++;  //要维持数组  指针。 size 是当前数组中的个数。
 45         */
 46         //此时其实可以直接复用 insert ()函数
 47         insert(this.size,num);
 48     }
 49     // 向数组头添加元素 （直接复用  向指定位置添加元素的函数 ）
 50     public void addFirst(T num){
 51         insert(0,num);
 52     }
 53 
 54     //向 指定数组位置添加一个新元素
 55     public void insert(int idx,T num){
 56         if(this.size == this.data.length){
 57 //            throw new IllegalArgumentException("数组已经放满了");
 58             /*此时对其扩容*/
 59             resize(2*this.data.length);
 60 
 61 
 62         }
 63         if(idx <0 || idx > this.size )
 64             throw new IllegalArgumentException("索引非法");
 65 
 66         for(int i=this.size-1;i >= idx;--i){
 67             this.data[i+1] = this.data[i];
 68         }
 69         this.data[idx] = num;
 70         //更新size
 71         this.size ++;
 72     }
 73 
 74     //////////////////////删///////////////////////////////////////
 75     //删除第一个
 76     public T removeFirst(){
 77         return remove(0);  //删除并将之返回出去
 78     }
 79 
 80     //删除最后一个
 81     public T removeLast(){
 82         return remove(this.size-1);
 83     }
 84 
 85     //删除指定位置  的元素
 86     public T remove(int idx){  //返回 删除的元素
 87         if(idx < 0 || idx > this.size -1)
 88             throw new IllegalArgumentException("idx错误！");
 89         T temp = this.data[idx];
 90         for (int i =idx;i<this.size - 1;i++){
 91             this.data[i] = this.data[i+1];
 92         }
 93         this.size -- ;
 94 
 95         //动态减少   当数组中的元素少于空间的一半的时候，就缩减空间。
 96         if(this.size == this.data.length / 2){
 97             System.out.println("size = "+this.size);
 98 
 99             resize(this.data.length/2);
100         }
101         return temp;
102     }
103 
104     //删除 某个元素 不根据其位置  //它之所以返回void 是因为调用着已经知道的element ，所以没必要再返回出来了。
105     public void removeElement(T element){
106         //首先要 寻找是否有 element
107         int idx = find(element);
108         if(idx == -1){
109             throw new IllegalArgumentException("没有该元素");
110         }else{
111             remove(idx);
112         }
113     }
114 
115     //////////////////////改///////////////////////////////////////
116     //修改索引为 idx 的元素为 num
117     public void setByIndex(int idx,T num){
118         if(idx <0 || idx > this.size)
119             throw new IllegalArgumentException("idx 错误！");
120 
121         this.data[idx] = num;
122     }
123 
124 
125     //////////////////////查///////////////////////////////////////
126     //获取整个数组的概括
127     //重写 toString()  当打印arr 时候，就会调用该方法！
128     @Override
129     public String toString(){
130         StringBuilder res = new StringBuilder();
131         res.append(String.format("Array:size = %d,capacity = %d 
",this.size,this.data.length));
132         res.append('[');
133         for (int i =0 ;i<this.size;i++){
134             res.append(data[i]);
135             if(i != this.size -1)
136                 res.append(", ");
137         }
138         res.append(']');
139         return res.toString();
140     }
141     //获取idx 索引位置的 元素
142     public T getByIndex(int idx){
143         if (idx < 0 || idx >this.size) {
144             throw new IllegalArgumentException("索引传入错误！");
145         }
146         return this.data[idx];
147     }
148 
149     //////////////////////包含///////////////////////////////////////
150     public boolean contains(T num){
151         for (int i=0;i<this.size;i++){
152             if(this.data[i] == num){
153                 return true;
154             }
155         }
156         return false;
157     }
158     //////////////////////寻找////////////////////////////////////
159     public int find(T num){
160         //寻找数组中是否有 num  ,如果有返回其索引，反之 返回-1
161         for (int i =0;i<this.size;i++){
162             if(this.data[i] == num){
163                 return i;
164             }
165         }
166         return -1;
167     }
168     //////////////////////实现动态数组  resize()////////////////////////////////////
169     private void resize(int new_capacity){  //之所以  用 private 是不让用户调用， 数组如果空间不足会自己扩展的。
170         T[] new_data =(T[]) new Object[new_capacity];
171 
172         for (int i =0;i<this.size;i++){
173             new_data[i] = this.data[i];
174         }
175         //
176         this.data = new_data;  //此时新数组的size 不变 ， 新数组的length 也不用变
177     }
178 }

MyArray.java

  1 package zcb.demo03;
  2 
  3 public class MaxHeap<T extends Comparable<T>> {
  4     private MyArray<T> arr;
  5 
  6     // 构造函数
  7     public MaxHeap(int capacity){
  8         // 已知容量
  9         arr = new MyArray<>(capacity);
 10     }
 11     public MaxHeap(){
 12         arr = new MyArray<>();
 13     }
 14 
 15     // heapify 操作 （将任意一个数组 转化为 一个堆 ）  堆化  （构造函数）
 16     public MaxHeap(T[] arr1){
 17         arr = new MyArray<>();
 18         // 首先将 arr1  数组中所有元素 放到 动态数组中
 19         for (int i=0;i<arr1.length;i++){
 20             arr.addLast(arr1[i]);
 21         }
 22 
 23         //从 倒数第一个 非叶子结点  开始每次都 siftDown 下
 24         int idx = getIdx_par(arr.getSize() - 1);
 25         for (int i=idx;i >= 0;i--){
 26             // 每次都 siftDown 即可
 27             siftDown(i);
 28         }
 29     }
 30 
 31 
 32     // ///////////////////////////////构造函数 ///////////////////////////////////////////
 33 
 34 
 35     // 返回堆中的 元素个数
 36     public int getSize(){
 37         return arr.getSize();
 38     }
 39     // 堆中是否为空
 40     public boolean isEmpty(){
 41         return arr.isEmpty();
 42     }
 43     // 下面是三个 私有的辅助函数
 44     // 根据当前节点的索引 算出左孩子的索引 (数组从0 就存值)
 45     private int getIdx_left(int cur_idx){
 46 
 47         return (cur_idx + 1)*2;
 48     }
 49     // 根据当前节点的索引 算出右孩子的索引
 50     private int getIdx_right(int cur_idx){
 51 
 52         return (cur_idx + 1)*2 - 1;
 53     }
 54     // 根据当前节点的索引 算出父亲节点的索引
 55     private int getIdx_par(int cur_idx){
 56         if(cur_idx == 0){
 57             throw new IllegalArgumentException("根节点 没有父亲节点");
 58         }
 59         return (cur_idx - 1) /2;
 60     }
 61 
 62     // 向堆中添加 元素
 63     public void add(T t){
 64         arr.addLast(t);
 65         if(arr.getSize() == 1){
 66             // 不需要调整位置了
 67             return ;
 68         }
 69         // 调整位置 siftUp()
 70         siftUp(arr.getSize() - 1);
 71     }
 72     private void siftUp(int cur_idx){
 73         int par_idx = getIdx_par(cur_idx);
 74 
 75         while ( arr.getByIndex(cur_idx).compareTo( arr.getByIndex(par_idx) ) > 0 ){
 76             // 上浮
 77             T temp = arr.getByIndex(cur_idx);
 78             arr.setByIndex(cur_idx,arr.getByIndex(par_idx));
 79             arr.setByIndex(par_idx,temp);
 80 
 81             cur_idx = par_idx;
 82             if(cur_idx == 0)
 83                 break;
 84             par_idx = getIdx_par(cur_idx);
 85         }
 86     }
 87 
 88     // 从堆中 取出元素  （取出元素的时候，我们只取出 堆顶元素（最大的））
 89     public T removeMax(){
 90         if(arr.isEmpty()){
 91             return null;
 92         }
 93         T ret = arr.getByIndex(0);
 94         arr.setByIndex(0,arr.getByIndex(arr.getSize() - 1));
 95         arr.remove(arr.getSize() - 1);
 96 
 97         if(arr.getSize() == 1){
 98             // 此时不需要调整
 99             return arr.getByIndex(0);
100         }
101 
102         //进行 下沉调整 操作
103         siftDown(0);
104         return ret;
105     }
106     private void siftDown(int par_idx){        // 也可以不使用 递归 ！！！（使用循环   ）
107         int left_idx = getIdx_left(par_idx);
108         int right_idx = getIdx_right(par_idx);
109         if(left_idx > arr.getSize() -1 || right_idx > arr.getSize() -1){
110             return;
111         }
112         if(arr.getByIndex(par_idx).compareTo(arr.getByIndex(left_idx)) > 0 && arr.getByIndex(par_idx).compareTo(arr.getByIndex(left_idx)) >0 ){
113             return;
114         }
115         if(arr.getByIndex(left_idx).compareTo(arr.getByIndex(right_idx))> 0){
116            // 向左 交换
117             T temp = arr.getByIndex(par_idx );
118             arr.setByIndex(par_idx,arr.getByIndex(left_idx));
119             arr.setByIndex(left_idx,temp);
120             siftDown(left_idx);
121         }else{
122             // 向右 交换
123             T temp = arr.getByIndex(par_idx );
124             arr.setByIndex(par_idx,arr.getByIndex(right_idx));
125             arr.setByIndex(right_idx,temp);
126             siftDown(right_idx);
127         }
128     }
129 
130 
131     // replace 操作 (将堆顶的 元素替换为 t 并返回堆顶元素 )
132     public T replace(T t){
133         T ret = arr.getByIndex(0);
134         arr.setByIndex(0,t);
135         siftDown(0);
136 
137         return ret;
138     }
139 
140     @Override
141     public String toString() {
142         return arr.toString();
143     }
144 }

MaxHeap.java (replace + heapify)

其中 heapify 在构造函数中，

 1 package zcb.demo03;
 2 
 3 import java.util.ArrayList;
 4 
 5 public class test {
 6     public static void main(String[] args) {
 7 //        MaxHeap<Integer> heap = new MaxHeap<>();
 8 //        heap.add(62);
 9 //        heap.add(52);
10 //        heap.add(30);
11 //        heap.add(28);
12 //        heap.add(41);
13 //        heap.add(22);
14 //        heap.add(13);
15 //        heap.add(19);
16 //        heap.add(17);
17 //        heap.add(15);
18 //        heap.add(16);
19 //        System.out.println(heap);
20 
21 ////////////////////////////////////////////////////////////////////////////
22 //        int [] arr = {13,15,17,16,19,41,22,28,30,52,62}; 不可
23         Integer[] arr = {13,15,17,16,19,41,22,28,30,52,62};
24         MaxHeap<Integer> heap = new MaxHeap<>(arr);
25         System.out.println(heap);
26 
27 
28 
29 
30     }
31 
32 }

test.java

基于堆的优先队列：

优先队列就是个队列，接口还是之前的 Queue

1 package zcb.demo04;
2 
3 public interface Queue <T> {
4     public abstract void enqueue(T t);  //入队
5     public abstract T dequeue();  //出队
6     public abstract T getFront();  //队头
7     public abstract int getSize();  //得到队列中的实际长度
8     public abstract boolean isEmpty();  //是否为空。
9 }

Queue.java

  1 package zcb.demo04;
  2 
  3 import zcb.demo03.MyArray;
  4 
  5 public class MaxHeap<T extends Comparable<T>> {
  6     private MyArray<T> arr;
  7 
  8     // 构造函数
  9     public MaxHeap(int capacity){
 10         // 已知容量
 11         arr = new MyArray<>(capacity);
 12     }
 13     public MaxHeap(){
 14         arr = new MyArray<>();
 15     }
 16 
 17     // heapify 操作 （将任意一个数组 转化为 一个堆 ）  堆化  （构造函数）
 18     public MaxHeap(T[] arr1){
 19         arr = new MyArray<>();
 20         // 首先将 arr1  数组中所有元素 放到 动态数组中
 21         for (int i=0;i<arr1.length;i++){
 22             arr.addLast(arr1[i]);
 23         }
 24 
 25         //从 倒数第一个 非叶子结点  开始每次都 siftDown 下
 26         int idx = getIdx_par(arr.getSize() - 1);
 27         for (int i=idx;i >= 0;i--){
 28             // 每次都 siftDown 即可
 29             siftDown(i);
 30         }
 31     }
 32 
 33 
 34     // ///////////////////////////////构造函数 ///////////////////////////////////////////
 35 
 36 
 37     // 返回堆中的 元素个数
 38     public int getSize(){
 39         return arr.getSize();
 40     }
 41     // 堆中是否为空
 42     public boolean isEmpty(){
 43         return arr.isEmpty();
 44     }
 45     // 下面是三个 私有的辅助函数
 46     // 根据当前节点的索引 算出左孩子的索引 (数组从0 就存值)
 47     private int getIdx_left(int cur_idx){
 48 
 49         return (cur_idx + 1)*2;
 50     }
 51     // 根据当前节点的索引 算出右孩子的索引
 52     private int getIdx_right(int cur_idx){
 53 
 54         return (cur_idx + 1)*2 - 1;
 55     }
 56     // 根据当前节点的索引 算出父亲节点的索引
 57     private int getIdx_par(int cur_idx){
 58         if(cur_idx == 0){
 59             throw new IllegalArgumentException("根节点 没有父亲节点");
 60         }
 61         return (cur_idx - 1) /2;
 62     }
 63 
 64     // 向堆中添加 元素
 65     public void add(T t){
 66         arr.addLast(t);
 67         if(arr.getSize() == 1){
 68             // 不需要调整位置了
 69             return ;
 70         }
 71         // 调整位置 siftUp()
 72         siftUp(arr.getSize() - 1);
 73     }
 74     private void siftUp(int cur_idx){
 75         int par_idx = getIdx_par(cur_idx);
 76 
 77         while ( arr.getByIndex(cur_idx).compareTo( arr.getByIndex(par_idx) ) > 0 ){
 78             // 上浮
 79             T temp = arr.getByIndex(cur_idx);
 80             arr.setByIndex(cur_idx,arr.getByIndex(par_idx));
 81             arr.setByIndex(par_idx,temp);
 82 
 83             cur_idx = par_idx;
 84             if(cur_idx == 0)
 85                 break;
 86             par_idx = getIdx_par(cur_idx);
 87         }
 88     }
 89 
 90     // 从堆中 取出元素  （取出元素的时候，我们只取出 堆顶元素（最大的））
 91     public T removeMax(){
 92         if(arr.isEmpty()){
 93             return null;
 94         }
 95         T ret = arr.getByIndex(0);
 96         arr.setByIndex(0,arr.getByIndex(arr.getSize() - 1));
 97         arr.remove(arr.getSize() - 1);
 98 
 99         if(arr.getSize() == 1){
100             // 此时不需要调整
101             return arr.getByIndex(0);
102         }
103 
104         //进行 下沉调整 操作
105         siftDown(0);
106         return ret;
107     }
108     private void siftDown(int par_idx){        // 也可以不使用 递归 ！！！（使用循环   ）
109         int left_idx = getIdx_left(par_idx);
110         int right_idx = getIdx_right(par_idx);
111         if(left_idx > arr.getSize() -1 || right_idx > arr.getSize() -1){
112             return;
113         }
114         if(arr.getByIndex(par_idx).compareTo(arr.getByIndex(left_idx)) > 0 && arr.getByIndex(par_idx).compareTo(arr.getByIndex(left_idx)) >0 ){
115             return;
116         }
117         if(arr.getByIndex(left_idx).compareTo(arr.getByIndex(right_idx))> 0){
118            // 向左 交换
119             T temp = arr.getByIndex(par_idx );
120             arr.setByIndex(par_idx,arr.getByIndex(left_idx));
121             arr.setByIndex(left_idx,temp);
122             siftDown(left_idx);
123         }else{
124             // 向右 交换
125             T temp = arr.getByIndex(par_idx );
126             arr.setByIndex(par_idx,arr.getByIndex(right_idx));
127             arr.setByIndex(right_idx,temp);
128             siftDown(right_idx);
129         }
130     }
131 
132     // 查看 当前堆顶的 元素
133     public T getMax(){
134         if(arr.isEmpty())
135             return null;
136         return arr.getByIndex(0);
137     }
138 
139 
140     // replace 操作 (将堆顶的 元素替换为 t 并返回堆顶元素 )
141     public T replace(T t){
142         T ret = arr.getByIndex(0);
143         arr.setByIndex(0,t);
144         siftDown(0);
145 
146         return ret;
147     }
148 
149     @Override
150     public String toString() {
151         return arr.toString();
152     }
153 }

MaxHeap.java

 1 package zcb.demo04;
 2 
 3 public class PriorityQueue<T extends Comparable<T>> implements Queue<T> {
 4     // 优先队列的底层结构是 最大堆
 5     private MaxHeap<T> heap;
 6     // 构造函数
 7     public PriorityQueue(){
 8         heap = new MaxHeap<>();
 9     }
10 
11     // Queue 中的接口方法 实现//////////////////////
12     public  int getSize(){
13         return heap.getSize();
14     }
15     public  boolean isEmpty(){
16         return heap.isEmpty();
17     }
18 
19     // 查看优先队列 队首的 元素，其实就是底层结构中 堆顶的 元素
20     public  T getFront(){
21         return heap.getMax();
22     }
23 
24     // 优先队列 入队操作
25     public  void enqueue(T t){
26         heap.add(t);
27     }
28     // 优先队列 出队操作
29     public  T dequeue(){
30         return heap.removeMax();
31     }
32 
33 }

PriorityQueue.java

 1 package zcb.demo04;
 2 
 3 public class test {
 4     public static void main(String[] args) {
 5         PriorityQueue<Integer> priorityQueue = new PriorityQueue<>() ;
 6 
 7         for (int i=0;i<10;i++){
 8             priorityQueue.enqueue(i*10);
 9         }
10         System.out.println(priorityQueue.getFront());
11 
12         ////////////////////////////////////////////////
13         priorityQueue.dequeue();
14         System.out.println(priorityQueue.getFront());
15 
16         ///////////////////////////////////
17         System.out.println(priorityQueue.getSize());
18 
19         ///////////////////////////////////
20         priorityQueue.enqueue(111);
21         System.out.println(priorityQueue.getFront() );
22 
23     }
24 }

test.java

优先队列的经典问题：

如何在100 000 个元素中选出前100名？（这类问题就是如何在 N个元素中选出 M个元素），

我们可以使用快速排序，它们时间复杂度是 nlogn ，然后再选出前 M个，这也是可以接受的，

现在的问题是有没有更好的方法来解决这类问题，

方法就是使用 优先队列 ，它的时间复杂度是 nlogM ,

具体是先将前M个元素放入优先队列，然后，再继续往里放，但是，优先队列一直要维持 M个元素，

具体例子看下题：

优先队列的应用 Leetcode No.347. 前k个高频元素：

注：java 自带的priorityqueue 默认是最小堆~ 它的构造函数可以传入一个比较器~

 1 package zcb.demo04;
 2 import java.util.LinkedList;
 3 import java.util.List;
 4 import java.util.TreeMap;
 5 import java.util.PriorityQueue;
 6 public class test {
 7     public static void main(String[] args) {
 8 //        输入: nums = [1,1,1,2,2,3], k = 2
 9 //        输出: [1,2]
10         int[] nums = {1,1,1,2,2,3};
11         List<Integer>ret  =  Solution.topKFrequent(nums,2);
12         System.out.println(ret);
13     }
14 }
15 
16 
17 class Solution {
18     public static List<Integer> topKFrequent(int[] nums, int k) {
19         TreeMap<Integer,Integer> map = new TreeMap<>();
20         for (int num :nums){
21             if(!map.containsKey(num)){
22                 map.put(num,1);
23             }else{
24                 map.put(num,map.get(num) + 1);
25             }
26         }
27         PriorityQueue<Integer> pq = new PriorityQueue<>(
28                 (a,b) -> map.get(a) - map.get(b)
29         );
30         for (int key:map.keySet()){
31             if(pq.size() < k)
32                 pq.add(key);
33             else if(map.get(key) > map.get(pq.peek()) ){
34                 pq.remove();
35                 pq.add(key);
36             }
37         }
38 
39         LinkedList<Integer> res = new LinkedList<>();
40         while (!pq.isEmpty()){
41             res.addFirst(pq.remove());
42         }
43         return res;
44     }
45 }

test.java

堆的扩展：

我们这里的基本上都是二叉堆，实际上计算机的世界中有很多形式多样的堆，

d 叉堆，这里的d 是一个节点有d个孩子，此时的时间复杂度更低（log d(n) ）,但是，此时在做下沉（siftDown ）的时候，便更复杂一些了，

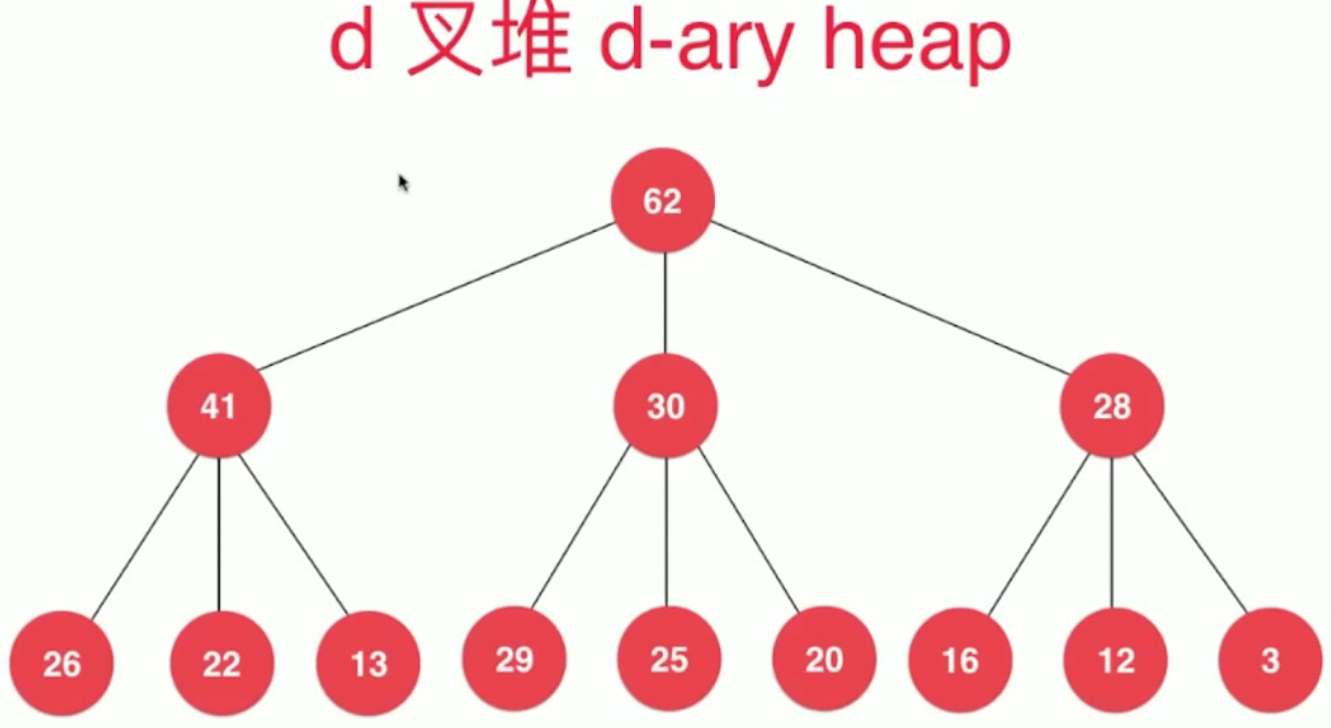
我们这里的堆是只能看到堆首的元素，不可以看到堆中间的元素，有时也是要看到堆中间的元素的，即 索引堆，（也保存它的索引，通过索引可以便捷的检索中间的元素并可以修改它）

索引堆： https://www.cnblogs.com/dudududu/p/8574740.html

还有二项堆，斐波那契堆，

相关阅读:
GDOI2017 之后
 [codevs1378]选课
 图的连通_Tarjan
[bzoj1270 BJWC2008]雷涛的小猫
 [51mod 1201]整数划分 dp
这只是一个非常水的人，写下的非常水的文字，不看也罢
 Python基础中所出现的异常报错总结
 Python简单爬虫入门二
 Python写地铁的到站的原理简易版
 HTML基本组成结构与标签的认识
原文地址：https://www.cnblogs.com/zach0812/p/11831890.html

最新文章
bzoj 4199
bzoj 3238
bzoj 1031
codevs 3160
bzoj 1072
bzoj 1076
bzoj 1875
bzoj 2301
bzoj 1257
poj3292-Semi-prime H-numbers(筛法打表)

01玩转数据结构_08_堆和优先队列

堆：

什么是优先队列：

堆的 基本结构：

二叉堆：

实现堆的 底层结构：

堆的时间复杂度：

堆上的另外两个 操作 replace 和 heapify：

基于 堆 的优先队列：

优先队列的经典 问题 ：

优先队列的应用 Leetcode No.347. 前k个高频元素：

堆的扩展：

堆的基本结构：

实现堆的底层结构：

堆上的另外两个操作 replace 和 heapify：

基于堆的优先队列：

优先队列的经典问题：