题目描述:
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。要求空间复杂度为$O(1)$
题解:
方案一使用环状替换:
如果我们直接把每一个数字放到它最后的位置,但这样的后果是遗失原来的元素。因此,我们需要把被替换的数字保存在变量$temp$里面。然后,我们将被替换数字($temp$)放到它正确的位置,并继续这个过程$n$次,$n$是数组的长度。但是,这种方法可能会有个问题,如果 $n%k == 0$,其中$k = k%n$(因为如果$k$大于$n$,移动$k$次实际上相当于移动$k%n$次)。这种情况下,我们会发现在没有遍历所有数字的情况下回到出发数字。此时,我们应该从下一个数字开始再重复相同的过程。流程如下图所示:
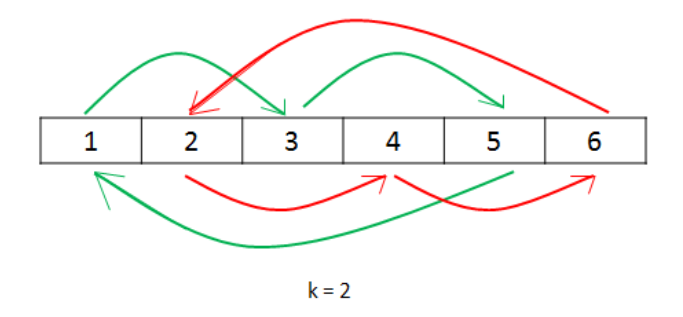
代码如下:
public void rotate(vector<int>& nums, int k) { k = k % nums.size(); int count = 0; for (int start = 0; count < nums.size(); start++) { int current = start; int prev = nums[start]; do { int next = (current + k) % nums.size(); int temp = nums[next]; nums[next] = prev; prev = temp; current = next; count++; } while (start != current); } }
方案二反转:
这个方法基于这个事实:当我们旋转数组$k$次,$k%n$个尾部元素会被移动到头部,剩下的元素会被向后移动。在这个方法中,我们首先将所有元素反转。然后反转前$k$个元素,再反转后面$n-k$个元素,就能得到想要的结果。代码如下:
class Solution { public: void rotate(vector<int>&nums, int k) { int n = nums.size(); k %= n; reverse(nums.begin(),nums.end()); reverse(nums.begin(),nums.begin()+k); reverse(nums.begin()+k,nums.end()); } };