poj2318 TOYS

传送门

给一个矩形和n块隔板,m个点 问隔板隔开的每个区域内有多少个点(保证不在隔板上)

n<=5000,m<=5000

首先考虑如果所有板子都是直的就是一个二分查找的标准形式

其实斜的也能一样做 因为二分的条件没变

变得就是如何判断在板子的左侧之类的

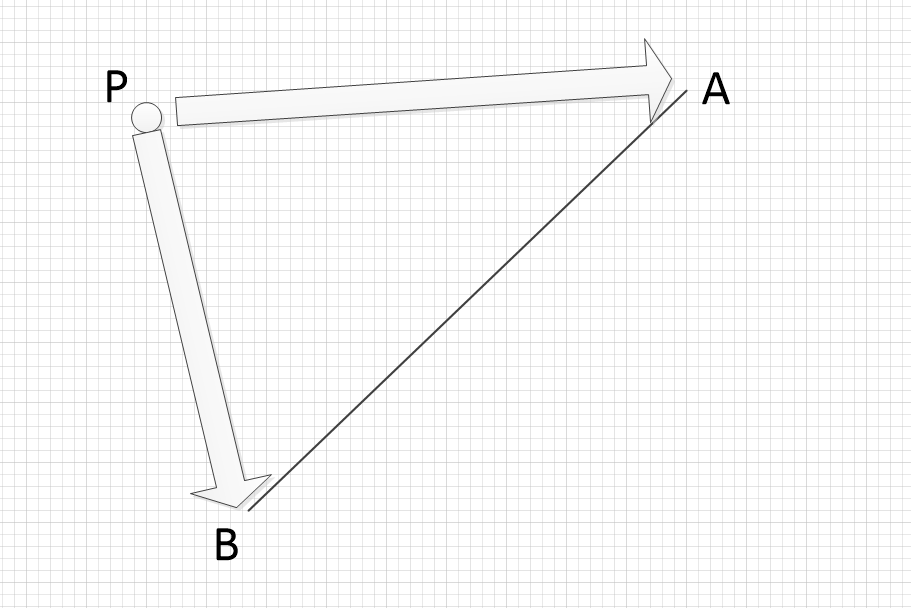
一个叉积就好了

图源自dalao https://blog.csdn.net/yskyskyer123/article/details/52107419

就是Xmlt(PA,PB)<0因为卡格所以没有共线的问题吧

复杂度O(mlgn*浮点常数)

Code:

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#include<iostream>
#define ms(a,b) memset(a,b,sizeof a)
#define rep(i,a,n) for(int i = a;i <= n;i++)
#define per(i,n,a) for(int i = n;i >= a;i--)
#define inf 2147483647
using namespace std;
typedef long long ll;
typedef double D;
#define eps 1e-8
ll read() {
    ll as = 0,fu = 1;
    char c = getchar();
    while(c < '0' || c > '9') {
        if(c == '-') fu = -1;
        c = getchar();
    }
    while(c >= '0' && c <= '9') {
        as = as * 10 + c - '0';
        c = getchar();
    }
    return as * fu;
}
//head
#define P point
struct point {
    D x,y;
    point(){}
    point(D X,D Y):x(X),y(Y){}
    D len() {return sqrt(x*x+y*y);}
    D tan() {return y/x;}
    D sin() {return len() / y;}
    D cos() {return len() / x;}
    void read() {scanf("%lf%lf",&x,&y);}
    void print() {printf("%.2lf %.2lf
",x,y);}
    friend inline point operator + (const point &a,const point &b) {
        return point(a.x+b.x,a.y+b.y);
    }
    friend inline point operator - (const point &a,const point &b) {
        return point(a.x-b.x,a.y-b.y);
    }
    //放缩
    friend inline point operator * (const point &a,const D &b) {
        return point(a.x*b,a.y*b);
    }
    //叉积
    friend inline D operator * (const point &a,const point &b) {
        return a.x*b.y-a.y*b.x;
    }
    //点积
    friend inline D operator / (const point &a,const point &b) {
        return a.x*b.x+a.y*b.y;
    }
};
struct line {
    D k,b;
    void init(point x,point y) {
        k = (y.y-x.y)/(y.x-x.x);
        b = x.y - k * x.x;
    }
    D YY(D X) {return k*X+b;}
    D XX(D Y) {return (Y-b)/k;}
};
struct yuan {
    D r,x,y;
    yuan(){}
    yuan(int R,int X,int Y):r(R),x(X),y(Y){}
};
bool ONSEG(point a,point b,point p) {
    return ((a-b).len() == (a-p).len() + (p-b).len());
}
D TRIAREA(point a,point b,point c) {
    return ((a-b)*(a-c)) / 2.0;
}
#define ONLINE(a,b,c) (((a-b)*(a-c)) == 0)
#define sign(x) (x) > 0 ? 1 : ((x) < 0 ? -1 : 0)
// 1  0 -1
// 锐 直 钝
int ANGDIR(point a,point b,point p) {
    D ans = (p-a)*(p-b);
    return sign(ans);
}

D dis(point a,point b,point p) {
    if(ANGDIR(b,p,a) == -1) return (p-a).len();
    if(ANGDIR(a,p,b) == -1) return (p-b).len();
    return ((p-a)*(p-b)) / (a-b).len();
}
D dis(point a,line l) {
    return (l.k * a.x - a.y + l.b) / sqrt(l.k*l.k+1);
}
int cross(P a,P b,P c,P d) {
    if(ONLINE(a,b,c) ^ ONLINE(a,b,d)) return 1;
    if(ONLINE(c,d,a) ^ ONLINE(c,d,b)) return 1;
    if(ONLINE(a,b,c) & ONLINE(a,b,d)) return -1;
    if(ONLINE(c,d,a) & ONLINE(c,d,b)) return -1;
    D J1 = ((c-d)*(c-a)) * ((c-d)*(c-b));
    D J2 = ((a-b)*(a-c)) * ((a-b)*(a-d));
    if(J1 < 0 && J2 < 0) return 1;
    return 0;
}
point Cross(point a,point b,point c,point d) {
    if(ONLINE(a,b,c)) return c;
    if(ONLINE(a,b,d)) return d;
    if(ONLINE(c,d,a)) return a;
    if(ONLINE(c,d,b)) return b;
    D S1 = (a-c)*(a-d),S2 = (b-d) * (b-c);
    point tmp = (b-a) * (S1 / (S1+S2));
    return a + tmp;
}
//CP
const int N = 100003;
int n,T;
D X1,Y1,X2,Y2;
int cnt[N];
struct seg {
    point a,b;
}p[N];
point aim;
bool check(int i) {
    return (aim - p[i].a) * (aim - p[i].b) < 0;
}

void solve() {
    aim.read();
    int L = 0,R = n+1;
    while(R > L) {
        int m = L+R >> 1;
        if(check(m)) R = m;
        else L = m+1;
    }
    cnt[L]++;
}

int main() {
    while(1) {
        n = read();
        if(!n) return 0;
        T = read();
        X1 = read(),Y1 = read(),X2 = read(),Y2 = read();
        rep(i,1,n) {
            p[i].a = point(read(),Y1);
            p[i].b = point(read(),Y2);
        }
        ms(cnt,0);
        rep(i,1,T) solve();
        rep(i,1,n+1) printf("%d: %d
",i-1,cnt[i]);
        puts("");
    }
}

一堆函数没什么用qwq