胜者树与败者树
胜者树和败者树都是完全二叉树,是树形选择排序的一种变型。每个叶子结点相当于一个选手,每个中间结点相当于一场比赛,每一层相当于一轮比赛。
不同的是,胜者树的中间结点记录的是胜者的标号;而败者树的中间结点记录的败者的标号。
胜者树与败者树可以在log(n)的时间内找到最值。任何一个叶子结点的值改变后,利用中间结点的信息,还是能够快速地找到最值。在k路归并排序中经常用到。
胜者树:
胜者树的一个优点是,如果一个选手的值改变了,可以很容易地修改这棵胜者树。只需要沿着从该结点到根结点的路径修改这棵二叉树,而不必改变其他比赛的结果。
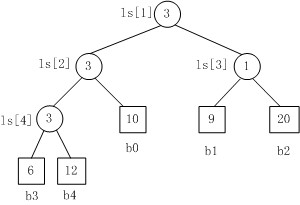
Fig. 1
Fig.1是一个胜者树的示例。规定数值小者胜。
1. b3 PK b4,b3胜b4负,内部结点ls[4]的值为3;
2. b3 PK b0,b3胜b0负,内部结点ls[2]的值为3;
3. b1 PK b2,b1胜b2负,内部结点ls[3]的值为1;
4. b3 PK b1,b3胜b1负,内部结点ls[1]的值为3。.
当Fig. 1中叶子结点b3的值变为11时,重构的胜者树如Fig. 2所示。
1. b3 PK b4,b3胜b4负,内部结点ls[4]的值为3;
2. b3 PK b0,b0胜b3负,内部结点ls[2]的值为0;
3. b1 PK b2,b1胜b2负,内部结点ls[3]的值为1;
4. b0 PK b1,b1胜b0负,内部结点ls[1]的值为1。.
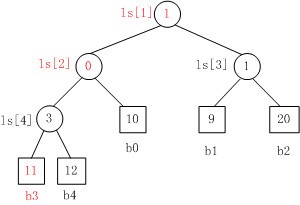
Fig. 2
败者树:
败者树是胜者树的一种变体。在败者树中,用父结点记录其左右子结点进行比赛的败者,而让胜者参加下一轮的比赛。败者树的根结点记录的是败者,需要加一个结点来记录整个比赛的胜利者。采用败者树可以简化重构的过程。
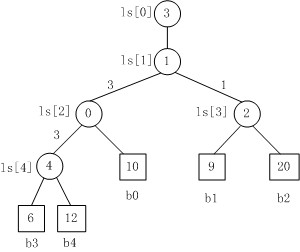
Fig. 3
Fig. 3是一棵败者树。规定数大者败。
1. b3 PK b4,b3胜b4负,内部结点ls[4]的值为4;
2. b3 PK b0,b3胜b0负,内部结点ls[2]的值为0;
3. b1 PK b2,b1胜b2负,内部结点ls[3]的值为2;
4. b3 PK b1,b3胜b1负,内部结点ls[1]的值为1;
5. 在根结点ls[1]上又加了一个结点ls[0]=3,记录的最后的胜者。
败者树重构过程如下:
· 将新进入选择树的结点与其父结点进行比赛:将败者存放在父结点中;而胜者再与上一级的父结点比较。
· 比赛沿着到根结点的路径不断进行,直到ls[1]处。把败者存放在结点ls[1]中,胜者存放在ls[0]中。
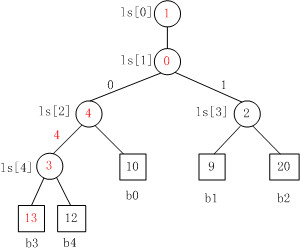
Fig. 4
Fig. 4是当b3变为13时,败者树的重构图。
注意,败者树的重构跟胜者树是不一样的,败者树的重构只需要与其父结点比较。对照Fig. 3来看,b3与结点ls[4]的原值比较,ls[4]中存放的原值是结点4,即b3与b4比较,b3负b4胜,则修改ls[4]的值为结点3。同理,以此类推,沿着根结点不断比赛,直至结束。
由上可知,败者树简化了重构。败者树的重构只是与该结点的父结点的记录有关,而胜者树的重构还与该结点的兄弟结点有关。
对一个数组使用构建其败者树
代码如下:
package struct.tree; import java.util.Random; /** * 败者树 * 父节点中只存放败者 */ public class LoserTree { public static int[] tree = null; public static int[] data = null; public static void main(String[] args) { int data_len = 10; data = new int[data_len]; Random rd = new Random(); for (int index = 0; index < data_len; index++) { data[index] = rd.nextInt(10000); } for (int i = 0; i < data.length; ) { System.out.printf("%d ", data[i++]); } System.out.println(); //初始化败者树,败者树的长度和叶子节点个数相同 tree = new int[data_len]; //指定败者树头的值 tree[0] = createLoserTree(1); for (int i = 0; i < tree.length; ) { System.out.printf("%d ", tree[i++]); } System.out.println(); data[2] = 2; adjust(2); for (int i = 0; i < tree.length; ) { System.out.printf("%d ", tree[i++]); } } /** * 创建败者树,返回胜利者,败者赋值给treeIndex节点 * 要设置treeIndex 的值必须先计算其子节点的值,依次递归,直到叶子节点 * * @param treeIndex 计算该节点值 * @return 胜者下标 */ public static int createLoserTree(int treeIndex) { //将树组下标影射到叶子节点 if (treeIndex >= tree.length) return treeIndex - tree.length; int left = treeIndex * 2; int right = treeIndex * 2 + 1; int leftWinner = createLoserTree(left); int rightWinner = createLoserTree(right); if (data[leftWinner] < data[rightWinner]) { tree[treeIndex] = rightWinner; return leftWinner; } else { tree[treeIndex] = leftWinner; return rightWinner; } } /** * 调整败者树 * * @param s 需要调整的下标 */ public static void adjust(int s) { for (int t = (s + tree.length) / 2; t > 0; t /= 2) { //当前值大于其父节点值 if (data[s] > data[t]) { int tmp = s; s = tree[t]; tree[t] = tmp; } } tree[0] = s; } }