广义线性模型
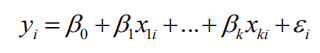
GLM是一般线性模型的扩展,它处顺序和分类因变量。
所有的组件都是共有的三个组件:
随机分量
系统分量
链接函数
===============================================
随机分量
随机分量跟随响应Y的概率分布
例1. (Y1,Y2,。....YN)可能是正态的。在这种情况下,我们会说随机分量是正态分布。该成分导致了普通回归和方差分析。
例2. y是Bernoulli随机变量(其值为0或1),即随机分量为二项分布时,我们通常关注的是Logistic回归模型或Proit模型。
例2. y是计数变量1,2,3,4,5,6等,即y具有泊松分布,此时的连接函数时ln(E(y)),这个对泊松分布取对数的操作就是泊松回归模型。
============================================
系统分量
系统组件将解释变量x1、x2、···、xk作为线性预测器:

============================================
连接函数
GLM的第三分量是随机和系统分量之间的链路。它表示平均值µ=e(y)如何通过指定函数关系g(µ)到线性预测器中的解释性变量

称G(μ)为链接函数..
==============================================
广义线性模型
Y被允许从指数型分布族中得到一个分布。
链路函数G(μI)是任何单调函数,并且定义了μI和Xβ之间的关系。

=================================================
逻辑回归
因变量是二进制的
评估多个解释变量(可以是数值型变量和/或类别型变量)对因变量的影响。
=============================================
模型含义:鸟类的巢址使用

响应变量是有巢的站点的概率,其中概率计算为p/(1-p),p是有巢的站点的比例。统计模型是

其中n是解释变量的个数,误差与p的二项分布一致。Odds的对数被称为P的Logit变换。
=====================================
Logit的优势
线性回归模型的性质
logit(P):介于负无穷和正无穷之间
概率(P)约束在0到1之间的

直接与事件的几率有关
====================================
前提:
必要的:
因变量是二进制的或二进位的。
这些病例是独立的
自变量不是彼此的线性组合。
不必要的:
独立变量各级相关变量的群体均值不在直线上,即不要求线性
误差的方差不是恒定的,即不要求方差的同质性
正态,即不要求误差分布是正态分布。
===========================================
例如:
通过年龄发展冠心病(CD)的风险(<60岁和>60岁)

病人中老年人的的比例28/11
病人中年轻人的的比例23/72
Odds ratio7.97
============================================
Logistic回归模型
β是在X中增加一个单位的几率对数
假设β=0的假设的测试

用比数比推测系数
是否拥有汽车作为收入的函数。
17个个人,14个拥有汽车,3个没有。
原始数据:

===============================
X变化的边际效应

斜率系数(单位)被解释为"对数赔率"随x变化的变化率...不是很有用
·我们也有兴趣看到解释变量对事件发生概率的影响
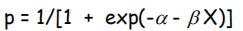
X对概率的边缘效应是

基本上,“边缘效应”的大小将取决于两个事物
β 参数
X最原始值
=======================================
边际效应:βXP(1-P)
考试及格或不及格取决于学习时数
先前的研究表明,α和β的估计值为

X初值在边际效应中的重要性
即使在相同的β条件下,边缘效应也是不同的,这取决于我们评价变化的地方。
从X的中心值开始变化对事件发生的概率的影响要比从非常低或非常高的X值开始时的影响更大。

β在确定边际效应方面有多重要?
正如我们已经看到的,β越大,曲线越陡。
因此,β越大,X的增加对事件发生概率的影响越大。

==============================================================
怎样评估模型参数?
最大似然估计
大多数统计方法被设计为最小化误差
选择最小化预测误差的参数值:
最大似然估计寻找最有可能产生观测分布的参数值。
例子:最大似然估计
用样本(4,6)估计人口平均数(SD=1),假设假设μ=3.5。在此假设下,4的概率密度为0.3521,6的概率密度为0.017,两概率的乘积是0.062。
接下来,假设假设为μ=4.0。在这种假设下,与两个观测相关的概率密度为0.3989和0.0540,而联合概率密度函数为0.0215。在μ=4.5的假设下,概率密度分别为0.3521和0.1295,联合概率密度为0.0456。
在μ=5.0的假设下,概率密度均为0.2420,联合概率密度为0.0585。
在假设μ=5.5时,概率密度分别为0.1295和0.3521,联合概率密度为0.0456。
的所有值的完整的联合密度函数现在都绘制在较低的图中。我们看到它在μ=5处达到峰值。
===============================================
联合密度:
在极大似然估计中,我们选择给出样本中观测值最大的联合密度的值作为的估计。该值与获取样本中观察结果的最大概率或最大似然相关
===============================================
似然函数
用其概率密度曲线定义模型:
其中,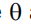 是pdf的参数,在抽样数据中为常数。
是pdf的参数,在抽样数据中为常数。
似然函数是

其中有n组样本数据。
(注意,x和 往往是向量)。
往往是向量)。
====================================
示例:投币式
N次独立硬币抛掷,k次在头部
二项分布,参数p
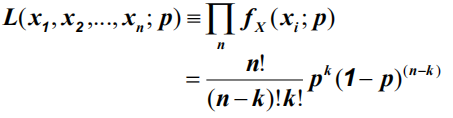
给定数据:100项试验,56头:
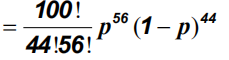

数值解产生最大P=0.56
参数的最大似然估计
对于MLE,目标是确定最有可能的总体参数值。给定观察到的样本值
任何模型的参数(例如,线性回归中的β,非线性模型中的a,b,c等)都可以用MLE估计。
似然函数是基于因变量分布的形状
Anova,Pearson‘s r,t检验,回归…假设样因变量的残差是正态分布的。在这些条件下,LSE(最小二乘估计)是最大似然估计。
如果因变量的残差不是正态分布,则LSE不是MLE。
=======================================
对于logistics回归的MLE
一个观察

似然函数


估计最大似然
在Logistic回归中,MLE是一种迭代算法,它从初始的任意“猜测”Logit系数开始,由MLE算法决定方向, Logit系数的大小变化,这将增加LL。
在对这个初始函数进行估计之后,对残差进行测试,用改进的函数进行重新估计,然后重复这个过程(通常大约六次),直到收敛为止。 达到了预期效果(也就是说,直到LL没有显著变化为止)。

=======================================
为什么不使用普通最小二乘(OLS)?
在Logistic回归中,相关的结果是事件发生的概率。
由于因变量(y)在0和1之间是有界的,所以OLS对二进制结果变量是不合适的。

====================================
全模型的拟合优度--似然比检验(LR)
我们比较模型中似然函数的值(与变量)和模型中似然函数的值(不含变量)。试验

其中,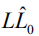 是空模型的对数似然(仅包括截距),
是空模型的对数似然(仅包括截距), 是全模型的对数似然((考虑到所有可变参数))
是全模型的对数似然((考虑到所有可变参数))
统计量分布为χ2,自由度与我们所限制的系数相同。
========================================
拟合优度-相似的
 指全平方之和
指全平方之和
 指回归平方和
指回归平方和
似然比指数


==================================
Hosmer-Lemesho统计量拟合优度
==============================
拟合优度-沃尔德试验
用WALD检验模型中各系数β的统计显着性。Wald测试计算Z统计量,即:

然后对这个z值进行平方,得到一个带有卡方分布的Wald统计量.
然而,有几位作者发现了使用Wald统计数据的问题。
===========================
逐步回归分析
简约原则:使用所需的最小数量的参数来适当地表示数据。
拟合优度随K(参数的数量)的增加而增加,折中。
低K:不足,错过重要影响
高K值:超适应,包括杂散效应和“噪音”
简约-在这两种效果之间保持适当的平衡,这样你就可以在不同的复制中重复结果。
=============================
Akaike信息准则
是为每个模型计算的数字。
提供了拟合模型与未知机制之间“距离”的估计,这个机制是产生真正数据的机制(“真相”)。
AIC值越低,模型越好。AIC值是相对的。
只能对完全相同的因变量集进行比较。
==========================
AIC=-2ln(似然)+2K
K=模型中的参数的数目,包括1个常数1和1个误差项

1.用于最小二乘回归、方差分析等

对于小样本(n/k<40),使用AICC,对小样本进行AIC校正。

===================================
何时使用AIC
主要是观察性研究,特别是具有大量变量的研究。
一般不会在实验研究中,因为你通常测试的效果相对较少,而且标准假设检验效果相当好。
======================================
回想一下什么是广义线性模型
y被允许从指数型分布族中得到一个分布
================================
一般线性模型
因变量是连续的,分布是正态的。
链接函数就是身份函数。
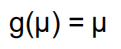
=====================
逻辑回归
因变量是离散的,分布是二项分布。
链接函数是logit。

===================
负二项分布
因变量是计数,分布是负二项分布。
链接函数是自然对数。

==========================
泊松回归
因变量是一个计数,分布是泊松分布。
链接函数是自然对数。

==================================
Poisson回归模型

响应变量y的泊松分布取决于预测变量。
默认的链接函数是log。

================================================
过分散
广义线性模型(GLMS)是一种简单、方便的计数数据模型,但它们假定方差是均值的一个指定函数。
过分散是二项分布和泊松数据偶尔出现的现象。对于泊松数据,当响应Y的方差大于泊松方差时,即如果模型是泊松分布,如果模型完全拟合则y的方差与均值应该都相同是一个定值λ,但是有时候观测值得到的方差和均值不同,这就是过分散。
 表示过分散(其中D是偏差,n是样本大小,p是变量数)
表示过分散(其中D是偏差,n是样本大小,p是变量数)
================================
广义混合模型(GLMM):空间自相关
广义线性模型的一种推广,其中线性预测器除了通常的固定效应外,还包含随机效应。
计数数据的零截断和零膨胀模型
零截断意味着响应变量的值不能为0。
医学文献中的一个典型例子是病人住院的时间。
要获取生态数据,可以考虑一些响应变量,如鲸鱼在重新淹没前到达水面的时间、鱼类上的鳍射线计数(例如用于鱼群识别)、海豚群的大小、动物的年龄(以年数或月为单位),或道路上杀死的动物的身体停留在路上的天数。
零膨胀数据在生态学研究中更为普遍。在这种情况下,根据泊松分布或负二项分布,响应变量包含的零点比预期的多。
=============================================
零截尾泊松分布
用于泊松分布的PDF:

为0的概率:

用于零截尾泊松分布的PDF:

=====================================================
零膨胀的GLM:为什么有这么多的零。
栖息地不合适
糟糕的实验设计或抽样实践
计算冬季悬崖上的海雀数量。很可能所有的样品都是0,因为这是一个错误的季节,他们都在海上。另一个设计错误是采样时间太短或采样面积太小。
观测者错误
有些鸟类看起来很相似,或者很难被发现。经验越少的观察者,他/她就越有可能获得难以识别的鸟类物种的零计数。或者,观察者可能是经验丰富的,但是在黑暗的日子里很难在黑暗的领域里发现一只微小的黑暗的鸟。
“动物”错误
这意味着栖息地是合适的,但该地点并没有被利用。
====================================
zip(Poisson)和ZINB(负二项式)模型
略
==================
ZIP模型
假设计数yi遵循泊松分布有期望值μi
用于泊松分布的PDF:

为0的概率:

假设Yi为假零的概率二项分布,概率πi,以下是ZIP模型的概率分布
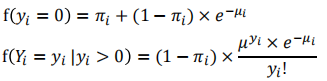
在PoissonGLM中,我们将正计数数据的平均数μI建模为

因此,协变量被用来模拟正计数。假零的概率是多少?πi?最简单的方法是使用logistic回归:
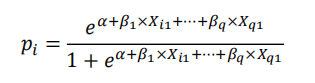
==========================================================
条件logistic回归
用于配对病例对照研究,例如:一个病例(读病)受试者与许多对照组(读非疾病)是基于一些匹配或混淆因素。
条件logistic回归
黑鼻猴科由一只公猴和几只母猴组成。单身男性(通常是青少年)有时会向家庭中的成年男性发起挑战,以取得控制权。
在一群黑鼻子猴中,大约有6-7个家庭,有42-60个个体。在过去的10年里,家庭成员不断变化。在此期间,共观察到48项挑战行为。
男性在一个家庭中受到挑战的概率,与其他5-6名未受挑战的男性相比,与家庭中的女性数量(F_Tot)、可用女性数量(未在怀孕或哺乳期)(F_Ava)以及男性的等级有关。
==============================================
多元Logistic
它是一种将Logistic回归推广到多类问题的分类方法,即具有两个以上可能的离散结果。
它假设观测到的特征和一些特定问题的参数的线性组合可以用来确定因变量的每个特定结果的概率。
它还有其他一些名字:
多元Logistic回归
多分类logistic回归
Softmax回归
多项Logit
=================================================
理论的说明:略
多元Logistic:略
有序Logistic回归:略
=============================================
多元线性回归:β1的解释是,其他x2----Xn都不发生改变(即这些变量被控制),只有x1发生改变,单位改变的x1使得y改变的该变量。用最小二乘法估计矩阵。只有所有向量都是线性独立才能计算特征值,所以之前要判断各变量之间确实没有多元共线性。
======================================
看整体x:决定系数是用于评判所有x变量对于y是不是有贡献对于多元线性模型的理解,可以把它认为是多元方差分析,它的决定系数是:
如果加入更多变量,则决定系数变更大,所以这就是R square不足的地方。于是提出 用来平衡模型的复杂程度。之前用F检验,检测一个β斜率,现在用F检验检测多个β斜率。
用来平衡模型的复杂程度。之前用F检验,检测一个β斜率,现在用F检验检测多个β斜率。
======================================
看单个x:贡献率:也可以单独挑出来单个变量,评判单变量对于y是否有贡献

看多个x:看两项合起来的因素组,对y的贡献情况,介于上两者之间。
==========================================
如果x有高次项,应该先设定成y=β0+β1x+β2x^2+β3x^3+β4x^4,而不是上来就写y=β0+β1x+β4x^4,因为存在高次项,所以一定会有多重共线性形成,即线性相关性。可以使用以下通式:

Piecewise线性关系就是每一段的斜率都不相同
Dummy variables用于比较多个组,把一个组作为基础组,其他组作为比较组,然后比较,它的解释是自变量是每一个斜率都是两类别变量下的连续值的差距。

=====================
数据转换
转换为正态分布
转换为方差齐性
转换为更简单的模型
不同y值类型与对应方程的选择:
