基于子阵列互累积量(Cross-Cumulant)的远场和近场混合声源定位[1]。
文中采用Uniform linear array (ULA)阵列,将其分为两个互相重叠的子阵列,构建关于子阵列输出信号的两个特殊cross-cumulant matrices,而这两个矩阵仅仅与源信号的DOA有关。
信号模型
阵列模型如下:

K个窄带信号,阵元数目为2M+1的对称ULA阵列。假设中间阵元为相位基准。则第m个传感器的接收信号可以表示为:
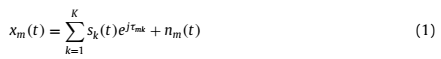
其中 为第k个入射信号的波形,
为第k个入射信号的波形, 为第m个传感器的噪声,
为第m个传感器的噪声, 为第k个源信号从阵元0到阵元m个传播时间(时延)。
为第k个源信号从阵元0到阵元m个传播时间(时延)。
当第k个入射信号是near-field信号时,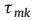 满足如下形式:
满足如下形式:
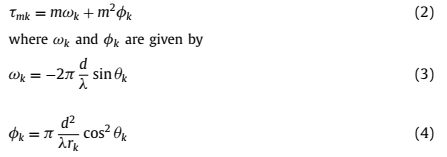
λ表示波长, 和
和 分别表示第k个源信号的DOA和range。根据菲涅耳区域的定义,
分别表示第k个源信号的DOA和range。根据菲涅耳区域的定义,![]() ,并且
,并且![]() 表示阵列孔径。
表示阵列孔径。
当第k个入射信号是far-field信号时,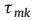 满足形式:
满足形式: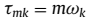
将公式(1)写为矩阵形式,可以表示为:

其中![]() 和
和![]() 是维度为
是维度为![]() 的复数向量,并且有:
的复数向量,并且有:
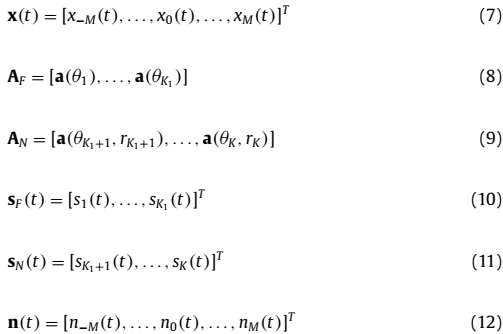
其中(2M + 1) × 1 的导向矢量表示为:
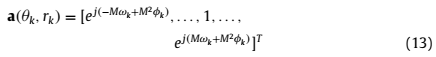
需要注意的是,在公式(6)表示的接收信号模型,前![]() 个源信号假定为FF源(近场源信号),剩余
个源信号假定为FF源(近场源信号),剩余![]() 个假定为NF源(远场源信号)。
个假定为NF源(远场源信号)。
本文有如下先验假设:
(1)源信号是统计独立的,采用非零峭度进行零均值随机处理。
(2)传感器噪声是加性的空间高斯白噪声,具有零均值。并且和源信号互相独立。
(3)已知源信号数目K,或者已经采用信息论准则准确估计得到。
提出算法
1、FF源和NF源的DOA估计
基于上述假设,阵列输出信号的四阶累计量表示为:
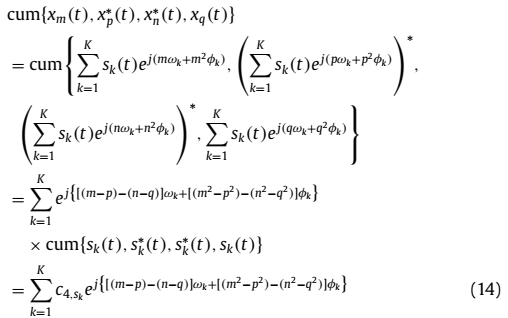
有 。其中第k个源信号的峭度表示为:
。其中第k个源信号的峭度表示为: 。
。
使得 ,
, ,公式(14)可以写作:
,公式(14)可以写作:
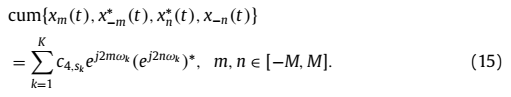
如图1所示,我们将ULA阵列划分为两个相互重叠的子阵列Y和Z,用以构建子阵列输出信号的cross-cumulant matrices,从此推导累积量的平移不变性。子阵列Y和Z的接收信号向量可以表示为:
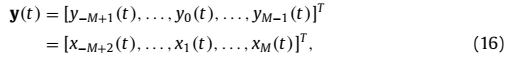

很明显地,y(t)的第m个元素为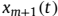 ,z(t)的第m个元素为
,z(t)的第m个元素为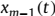 。
。
根据上述子阵列的输出信号和公式(15),可以构建两个互累积量矩阵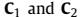 ,其第
,其第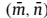 个元素为:
个元素为:
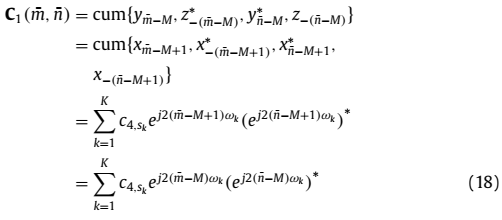

其中 。注意上述两个互累积量矩阵可以仅用DOAs表示。
。注意上述两个互累积量矩阵可以仅用DOAs表示。
C1表示为紧凑的矩阵形式:

其中 ,虚拟的“阵列流型矢量”为
,虚拟的“阵列流型矢量”为 ,并且
,并且
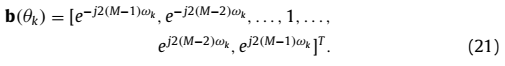
同理,C2可以表示为:

其中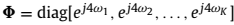 。
。
结合C1和C2,得到(4M - 2) × (4M - 2) 矩阵为:


对C进行特征值分解,得到:

其中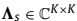 ,并且
,并且 是包含K个C的最大特征值以及(4M-2-K)个C的最小特征是的对角矩阵。
是包含K个C的最大特征值以及(4M-2-K)个C的最小特征是的对角矩阵。 和
和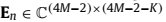 分别是对应的特征向量组成的矩阵。
分别是对应的特征向量组成的矩阵。
基于子阵列理论,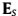 张成
张成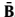 的列空间,这表示存在一个K×K的矩阵T使得:
的列空间,这表示存在一个K×K的矩阵T使得: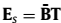 。
。
使得E1和E2为Es的最大和最小(2M-1)×K的半矩阵,由上式得到: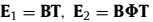 ,组成结果:
,组成结果:

其中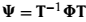 。公式(28)可以用TLS准则求解
。公式(28)可以用TLS准则求解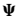 ,其特征值是和源信号的DOAs相关的。使得V为
,其特征值是和源信号的DOAs相关的。使得V为 的2K×2K的右奇异向量,当V被划分为4个K×K子阵列:
的2K×2K的右奇异向量,当V被划分为4个K×K子阵列:

则公式(28)的解可以给出:

假设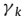 是
是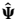 的第k个特征值,则第k个源信号的DOA可以给出:
的第k个特征值,则第k个源信号的DOA可以给出:
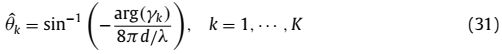
2、源辨识和距离估测
对接收信号的相关矩阵进行EVD,得到:

其中 和
和 分别为包含R的K个最大特征值和(2M+1-K)个最小特征值的对角矩阵。
分别为包含R的K个最大特征值和(2M+1-K)个最小特征值的对角矩阵。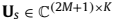 和
和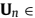
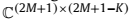 分别为对应的特征向量组成的矩阵。
分别为对应的特征向量组成的矩阵。
根据上述DOA估计值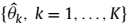 ,代入
,代入 到下述谱函数中:
到下述谱函数中:
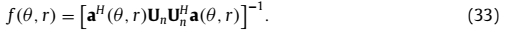
可以计算估计距离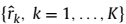 。
。
此处 和
和 无需其他处理,自动匹配。实际上,我们就可以辨别不同的源信号了,当
无需其他处理,自动匹配。实际上,我们就可以辨别不同的源信号了,当 时,第k个源为NF源;当
时,第k个源为NF源;当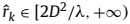 时为FF源,此时使得
时为FF源,此时使得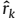 为
为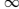 。
。
3、讨论
1)需要注意的是,为了避免 中的元素出现相位模糊性,文中提出算法要求
中的元素出现相位模糊性,文中提出算法要求 。
。
2)鉴于四阶累计量矩阵C1和C2的维度是2M-1,对于一个包含2M+1个真元的ULA,最多可以定位2M-2个不同源信号。不同的是,二阶MUSIC算法和高阶MUSIC算法可以分别最多处理M和2M个源信号。
3)对于文中提出方法,主要的计算量在于构建累积量矩阵,计算协方差矩阵,及其EVDs和距离搜索,需要乘法次数
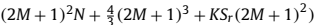 次,其中
次,其中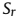 为在菲涅尔域内搜索点数。
为在菲涅尔域内搜索点数。
因为除了搜索距离,还需要估计DOAs,高阶MUSIC算法需要的乘法次数为
 。
。
二阶MUSIC算法需要的乘法次数为
 。其中
。其中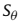 是在角度域中需要搜索的点数。
是在角度域中需要搜索的点数。
需要注意的是,文中所提方法的计算复杂度中没有 ,所以其计算复杂度低于高阶MUSIC。
,所以其计算复杂度低于高阶MUSIC。
仿真实验



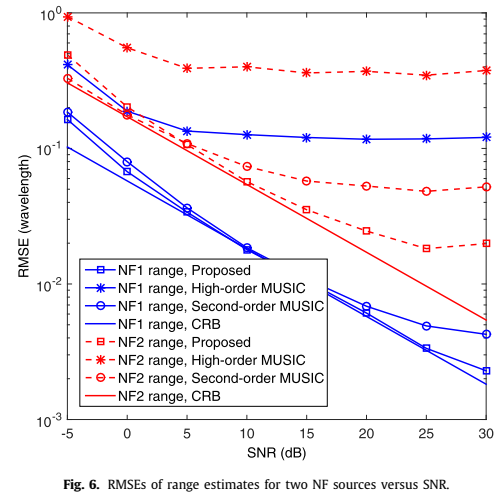
参考文献
[1] Zhi Zheng, Mingcheng Fu, Wen-Qin Wang,etc. Mixed Far-Field and Near-Field Source Localization Based on Subarray Cross-Cumulant ☆[J]. Signal Processing, 2018.