Expanding Rods
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 13516 | Accepted: 3484 |
Description
 When a thin rod of length L is heated n degrees, it expands to a new length L'=(1+n*C)*L, where C is the coefficient of heat expansion.
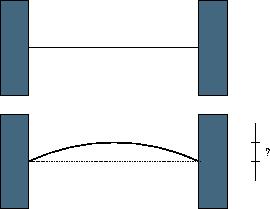
When a thin rod of length L is heated n degrees, it expands to a new length L'=(1+n*C)*L, where C is the coefficient of heat expansion. When a thin rod is mounted on two solid walls and then heated, it expands and takes the shape of a circular segment, the original rod being the chord of the segment.
Your task is to compute the distance by which the center of the rod is displaced.
Input
The
input contains multiple lines. Each line of input contains three
non-negative numbers: the initial lenth of the rod in millimeters, the
temperature change in degrees and the coefficient of heat expansion of
the material. Input data guarantee that no rod expands by more than one
half of its original length. The last line of input contains three
negative numbers and it should not be processed.
Output
For
each line of input, output one line with the displacement of the center
of the rod in millimeters with 3 digits of precision.
Sample Input
1000 100 0.0001 15000 10 0.00006 10 0 0.001 -1 -1 -1
Sample Output
61.329 225.020 0.000
题目:可以这样理解,给你一根木杆,夹在某物体之间。现在木杆会受热膨胀,膨胀增长,在两端物体的挤压下就会变弯曲,如上图所示。
从一根直的木杆变到弯曲的木杆,两种状态下,木杆中间位置的高度差是多少?
解法全在上面的图片中!
代码:
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <ctype.h>
#include <math.h>
#include <iostream>
#include <string>
#include <stack>
#include <algorithm>
#define eps 1e-5
using namespace std;
int main()
{
// L'=(1+n*C)*L
double L, n, c;
while(scanf("%lf %lf %lf", &L, &n, &c)!=EOF)
{
if(L<0 && n<0 && c<0) break;
double low=0.0;
double high=0.5*L;
double mid;
double s=(1.0+n*c)*L;
double R;
while(high-low>eps){
mid=(low+high)/2.0;
R = (4*mid*mid+L*L)/(8*mid);//化简成一次除法 减小精度误差
if(2*R*asin(L/(2*R)) < s)
low=mid;
else
high=mid;
}
printf("%.3lf
",mid);
}
return 0;
}
