树状数组(搬运自维基百科)

树状数组(Fenwick_tree)，最早由Peter M. Fenwick于1994年以A New Data Structure for Cumulative Frequency Tables为题发表在SOFTWARE PRACTICE AND EXPERIENCE。其初衷是解决数据压缩里的累积频率(Cumulative Frequency)的计算问题，现多用于高效计算数列的前缀和。它可以以的时间得到，并同样以对某项加一个常数。

基本操作:

　　1)新建；

　　2)修改；

　　3)求和；

lowbit求法：

int lowbit(int x)
{
    return x&(-x);
}

新建:

定义一个数组 BIT，用以维护的前缀和，则:

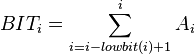
具体能用以下方式实现：

void build()
{
    for (int i=1;i<=MAX_N;i++)
    {
        BIT[i]=A[i];
        for (int j=i-1; j>i-lowbit(i); j--)
            BIT[i]+=A[j];
    }
}

修改:

假设现在要将的值增加delta,

那么,需要将覆盖的区间包含的值都加上K.

这个过程可以写成递归,或者普通的循环.

需要计算的次数与数据规模N的二进制位数有关,即这部分的时间复杂度是O(LogN)

void edit(int i, int delta)
{
    for (int j = i; j <= MAX_N; j += lowbit(j))
        BIT[j] += delta;
}

求和:

假设我们需要计算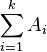的值.

1. 首先,将ans初始化为0，将i计为k.
2. 将ans的值加上BIT[P]
3. 将i的值减去lowbit(i)
4. 重复步骤2～3，直到i的值变为0

int sum (int k)
{
    int ans = 0;
    for (int i = k; i > 0; i -= lowbit(i))
        ans += BIT[i];
    return ans;
}