二分法其实很简单，为什么老是写不对！！

文章持续更新，微信搜索「代码随想录」第一时间围观，本文GitHub:https://github.com/youngyangyang04/TechCPP已经收录，里面有更多干货等着你，欢迎Star！

相信很多人对二分法是又爱又恨，爱是在于它思想简单，效率确实高， 恨是恨在为什么总是写不对呢

二分查找涉及的很多的边界条件，逻辑比较简单，就是写不好

甚至有的同学干脆把二分法背来了得了

其实背过的同学应该会有体会，硬背二分法，过一段时间依然会写错

例如 循环中到底是 小于 还是 小于等于， 到底是+1 呢，还是要-1呢

这是为什么呢，主要是我们对区间的定义没有想清楚，这就是我们的不变量

我们要在二分查找的过程中，保持不变量，这也就是循环不变量 （感兴趣的同学可以查一查）

接下来我通过leetcode上一道面试题，来让大家一次性彻底掌握二分法

题目是leetcode编号35的面试题. 搜索插入位置

 

题目地址:https://leetcode-cn.com/problems/search-insert-position/

分析题目

这道题目，我们要在数组中插入目标值，无非是这四种情况

 

 

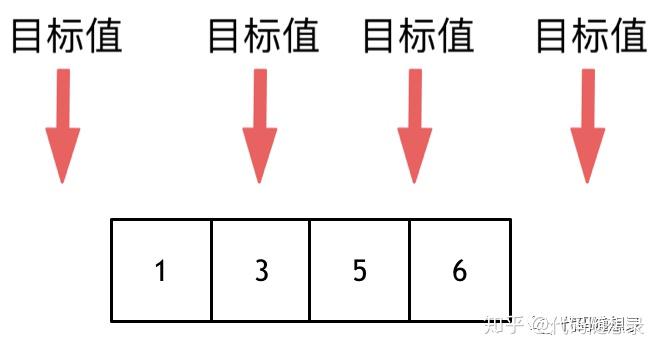
• 目标值在数组所有元素之前
• 目标值等于数组中某一个元素
• 目标值插入数组中的位置
• 目标值在数组所有元素之后

这四种情况确认清楚了，我们就可以尝试解题了

暴力解法思路很直接，就是for循环遍历一下，时间复杂度是O(n)

既然暴力解法的时间复杂度是On，我们就要尝试一下使用二分查找法。

二分法

大家注意这道题目的前提是数组是有序数组，这也是使用二分查找的基础条件

以后大家只要看到面试题里给出的数组是有序数组，都可以想一想是否可以使用二分法。

同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下表可能不是唯一的。

下图来阐述一下二分法的大体思路，例如在这个数组中，我们使用二分法寻找元素为5的位置，并返回其下标，如下图

 

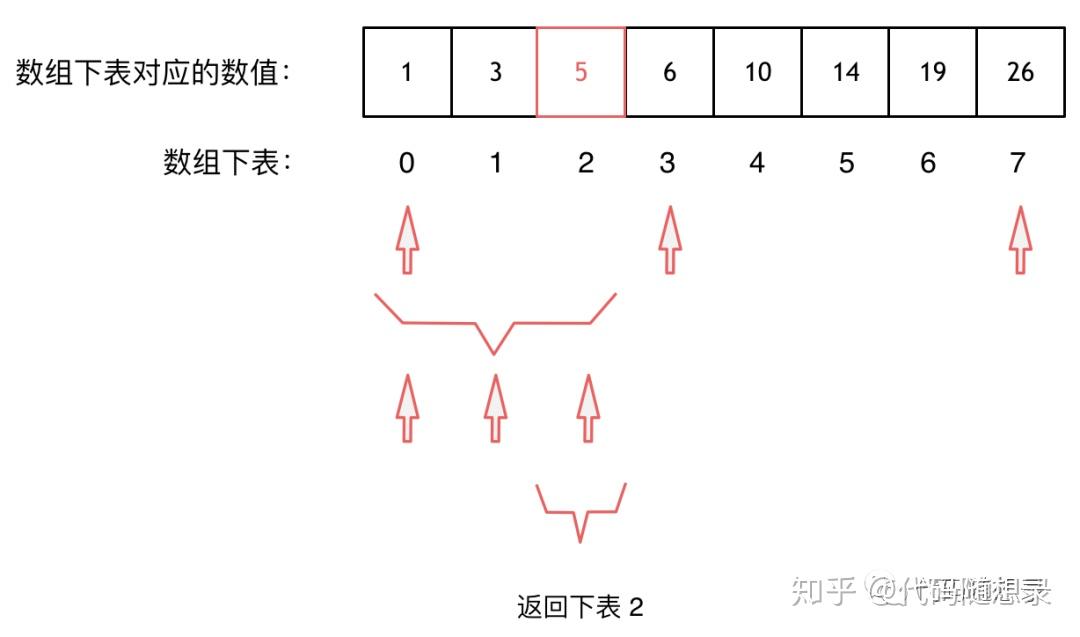
1. 开始左边界为0，右边界下表为7，那么中间位置下表是3， arr[3] > 5
2. 左区间为我们下一步的查找范围，
3. 左边界为0，右边界为2，中间位置下表为1 arr[1] < 5
4. 右区间为我们下一步的查找范围
5. 左边界2，右边界2，a[2] == 5，
6. 返回下表2。

接下来呢我们来看一下二分法具体实现

二分法第一种写法

我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right]

这就决定了我们 这个二分法的代码如何去写，大家看如下代码

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0;
        int right = n - 1; // 我们定义target在左闭右闭的区间里，[left, right]，这个区间的定义就是我们的不变量，接下来，要在下面的循环中，坚持这个不变量，我们就知道其中的边界条件应该怎么判断了
        while (left <= right) { // 为什么是<=呢，因为当left==right，区间[left, right]依然有效
            int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target 在左区间，因为我们的区间是左闭右闭的区间，nums[middle]一定不是我们的目标值，所以在right = middle - 1在[left, middle - 1]区间中继续寻找目标值
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle;
            }
        }
        // 分别处理如下四种情况
        // 目标值在数组所有元素之前，此时区间为[0, -1]，所以return right + 1
        // 目标值等于数组中某一个元素  return middle;
        // 目标值插入数组中的位置，一定是我们查找的范围 [left, right]之后，return  right + 1
        // 目标值在数组所有元素之后的情况，也是我们查找的范围 [left, right]之后， return right + 1
        return right + 1;
    }
};

时间复杂度：O(logn)
时间复杂度：O(1)

效率如下：

 

二分法第二种写法

如果说我们定义 target 是在一个在左闭右开的区间里，也就是[left, right)

那么二分法的边界处理方式则截然不同。

不变量是[left, right)的区间，如下代码可以看出是如何在循环中坚持不变量的。

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0;
        int right = n; // 我们定义target在左闭右开的区间里，[left, right)  这是
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target 在左区间，因为是左闭右开的区间，nums[middle]一定不是我们的目标值，所以right = middle，在[left, middle)中继续寻找目标值
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在 [middle+1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值的情况，直接返回下标
            }
        }
        // 分别处理如下四种情况
        // 目标值在数组所有元素之前，此时区间为 [0,0)，所以可以return right
        // 目标值等于数组中某一个元素 return middle
        // 目标值插入数组中的位置 [left, right) ，return right 即可
        // 目标值在数组所有元素之后的情况 [left, right)，return right 即可
        return right;
    }
};

时间复杂度：O(logn)
时间复杂度：O(1)

总结

从上面两种二分法的代码中，我们可以看到是如何处理二分查找过程中的边界情况

很多同学二分写不好，就是因为边界总是不知道 该是<= 还是< 呢，

是 right = middle - 1呢 还是 right = middle呢

这都是因为没有意识到去区间的定义，区间的定义就是我们的不变量

在二分部查找的过程只要遵循着区间的定义也就是这个不变量

我们就可以很轻松的写出二分法

以上讲解大家应该对二分法中循环不变量有一个直观的感受

理解的查找区间的定义（不变量），然后在二分循环中遇到了不知该如何处理的边界条件的时候

就去想一下 我们区间的定义，这样就知道边界条件应该如何去写了

通过这次讲解希望帮助大家可以彻底理解二分法！