一. 矩阵分解:
矩阵分解 (decomposition, factorization)是将矩阵拆解为数个矩阵的乘积,可分为三角分解、满秩分解、QR分解、Jordan分解和SVD(奇异值)分解等,常见的有三种:1)三角分解法 (Triangular Factorization),2)QR 分解法 (QR Factorization),3)奇异值分解法 (Singular Value Decompostion)。
- LU三角分解:
三角分解法是将原正方 (square) 矩阵分解成一个上三角形矩阵 或是排列(permuted) 的上三角形矩阵和一个 下三角形矩阵,这样的分解法又称为LU分解法。它的用途主要在简化一个大矩阵的行列式值的计算过程,求 反矩阵,和求解联立方程组。不过要注意这种分解法所得到的上下三角形矩阵并非唯一,还可找到数个不同 的一对上下三角形矩阵,此两三角形矩阵相乘也会得到原矩阵。
MATLAB以lu函数来执行lu分解法, 其语法为[L,U]=lu(A)。 - QR分解:
QR分解法是将矩阵分解成一个正规正交矩阵与上三角形矩阵,所以称为QR分解法,与此正规正交矩阵的通用符号Q有关。
MATLAB以qr函数来执行QR分解法, 其语法为[Q,R]=qr(A)。
3. 奇异值分解:
奇异值分解 (singular value decomposition,SVD) 是另一种正交矩阵分解法;SVD是最可靠的分解法,但是它比QR 分解法要花上近十倍的计算时间。[U,S,V]=svd(A),其中U和V分别代表两个正交矩阵,而S代表一对角矩阵。 和QR分解法相同, 原矩阵A不必为正方矩阵。使用SVD分解法的用途是解最小平方误差法和数据压缩。
MATLAB以svd函数来执行svd分解法, 其语法为[S,V,D]=svd(A)。 - LLT分解:
A=LL^T
Cholesky 分解是把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解。它要求矩阵的所有特征值必须大于零,故分解的下三角的对角元也是大于零的(LU三角分解法的变形)。
5. LDLT分解法:
若A为一对称矩阵且其任意一k阶主子阵均不为零,则A有如下惟一的分解形式:
A=LDL^T
其中L为一下三角形单位矩阵(即主对角线元素皆为1),D为一对角矩阵(只在主对角线上有元素,其余皆为零),L^T为L的转置矩阵。
LDLT分解法实际上是Cholesky分解法的改进,因为Cholesky分解法虽然不需要选主元,但其运算过程中涉及到开方问题,而LDLT分解法则避免了这一问题,可用于求解线性方程组。
二. 代码使用:
<span style="font-size:18px;">
#include <iostream>
#include <Eigen/Dense>
using namespace std;
using namespace Eigen;
int main()
{
//线性方程求解 Ax =B;
Matrix4d A;
A << 2,-1,-1,1, 1,1,-2,1, 4,-6,2,-2, 3,6,-9,7;
Vector4d B(2,4,4,9);
Vector4d x = A.colPivHouseholderQr().solve(B);
Vector4d x2 = A.llt().solve(B);
Vector4d x3 = A.ldlt().solve(B);
std::cout << "The solution is:
" << x <<"
"<<x2<<"
"<<x3 <<std::endl;
}
</span>
注意:
我用上面代码计算出来,只有A.colPivHouseholderQr().sole(B),算出来的是正常。其他都是错误,我就先使用这个公式运算吧,等我忙完这一阵子,在来研究一下。
运行结果:
colPivHouseholderQr:
0
-1
-4
-3
llt:
-289.143
448.714
29.9082
3.97959
ldlt:
1.52903
0.1758
-0.340206
0.0423223
除了colPivHouseholderQr、LLT、LDLT,还有以下的函数可以求解线性方程组,请注意精度和速度:解小矩阵(4*4)基本没有速度差别
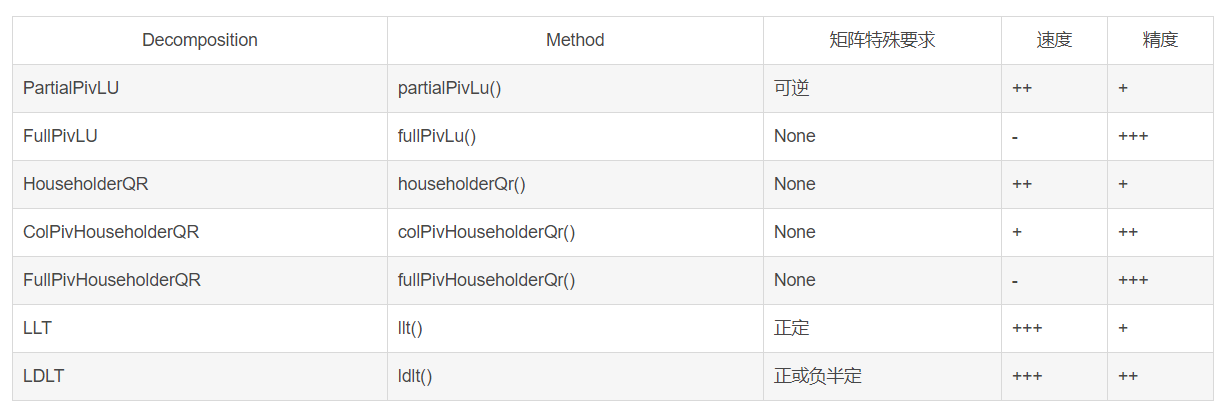
// Solve Ax = b. Result stored in x. Matlab: x = A b.
x = A.ldlt().solve(b)); // A sym. p.s.d. #include <Eigen/Cholesky>
x = A.llt().solve(b)); // A sym. p.d. #include <Eigen/Cholesky>
x = A.lu().solve(b)); // Stable and fast. #include <Eigen/LU>
x = A.qr().solve(b)); // No pivoting. #include <Eigen/QR>
x = A.svd().solve(b)); // Stable, slowest. #include <Eigen/SVD>
// .ldlt() -> .matrixL() and .matrixD()
// .llt() -> .matrixL()
// .lu() -> .matrixL() and .matrixU()
// .qr() -> .matrixQ() and .matrixR()
// .svd() -> .matrixU(), .singularValues(), and .matrixV()
本文转自 ChenYuanshen 的CSDN 博客 :https://blog.csdn.net/u013354805/article/details/48250547?utm_source=copy