【luoguP2252】 取石子游戏

题目链接

定义(f[i][j])表示(a=i，b=j)时是必胜态还是必败态，博弈DP可以解决(a,b leq 100) 的情况

然后就可以找规律了，发现(f[i][j]=0)的情况很少，所以打印出(f[i][j]=0)时的(i)和(j)的表

((i,j))和((j,i))是等价的，所以不妨只考虑(i<=j)的情况

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;

const int MAXN=10010;

int a,b,f[MAXN][MAXN];

bool dfs(int x,int y){
	if(f[x][y]!=-1) return f[x][y];
	if(x==0&&y==0) return f[x][y]=0;
	f[x][y]=0;
	for(int i=0;i<x&&!f[x][y];++i)
		if(!dfs(i,y)) f[x][y]=1;
	for(int i=0;i<y&&!f[x][y];++i)
		if(!dfs(x,i)) f[x][y]=1;
	int k=min(x,y);
	for(int i=1;i<=k&&!f[x][y];++i)
		if(!dfs(x-i,y-i)) f[x][y]=1;
	return f[x][y];
}

int main()
{
	memset(f,-1,sizeof(f));
//	scanf("%d%d",&a,&b);
//	if(dfs(a,b)) puts("1");
//	else puts("0");
	for(int i=1;i<=100;++i)
		for(int j=i;j<=100;++j)
			if(!dfs(i,j))cout<<i<<' '<<j<<endl;
	return 0;
}

发现表是这样的

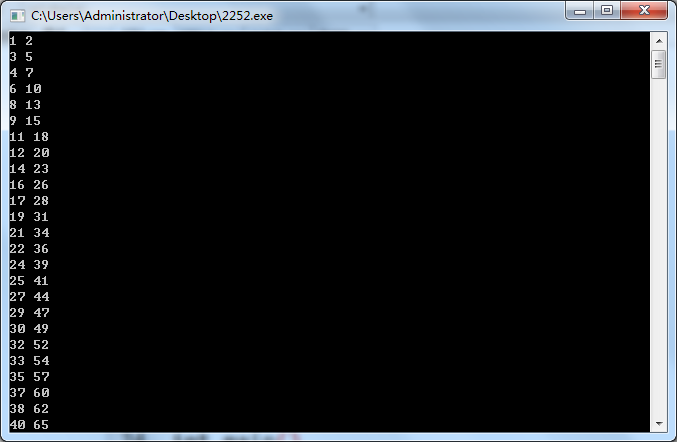
我们发现(i)和(j)似乎是成正比增长的，不妨输出j/i看看

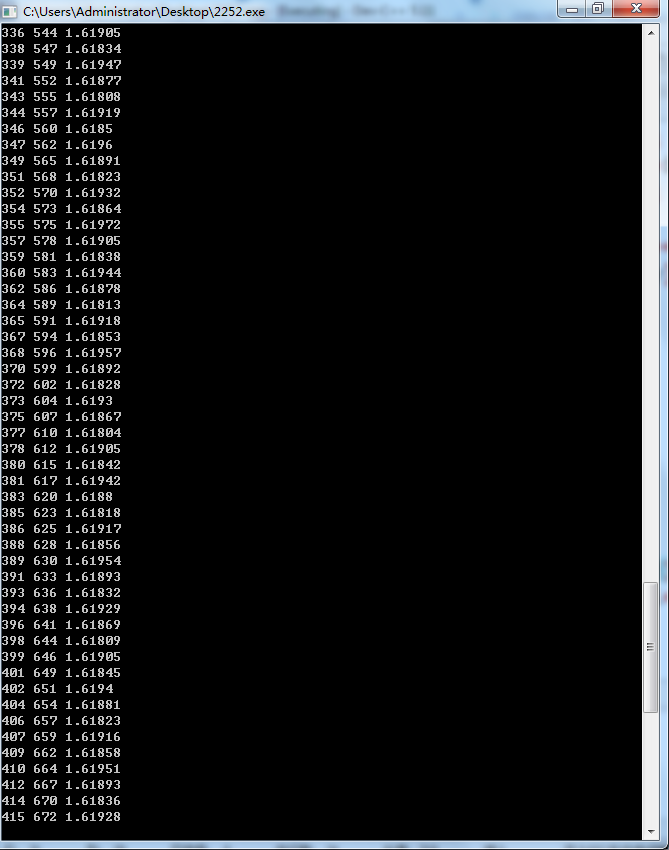
当(i，j)较大时大概稳定在略大于(6.18)的位置

于是就有了(AC)代码:

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;

int a,b;

int main()
{
	scanf("%d%d",&a,&b);
	if(a>b) swap(a,b);
	if(ceil(a*1.618)==b) puts("0");
	else puts("1");
	return 0;
}