实验二 K-近邻算法及应用
| 个人班级 | 机器学习实验-计算机182 |
|---|---|
| 实验题目 | K-近邻算法及应用 |
| 姓名 | 于俊杰 |
| 学号 | 3180701201 |
一、实验目的
理解K-近邻算法原理,能实现算法K近邻算法;
掌握常见的距离度量方法;
掌握K近邻树实现算法;
针对特定应用场景及数据,能应用K近邻解决实际问题。
二、实验内容
实现曼哈顿距离、欧氏距离、闵式距离算法,并测试算法正确性。
实现K近邻树算法;
针对iris数据集,应用sklearn的K近邻算法进行类别预测。
针对iris数据集,编制程序使用K近邻树进行类别预测。
三、实验过程及结果
一、实验代码及注释
1、
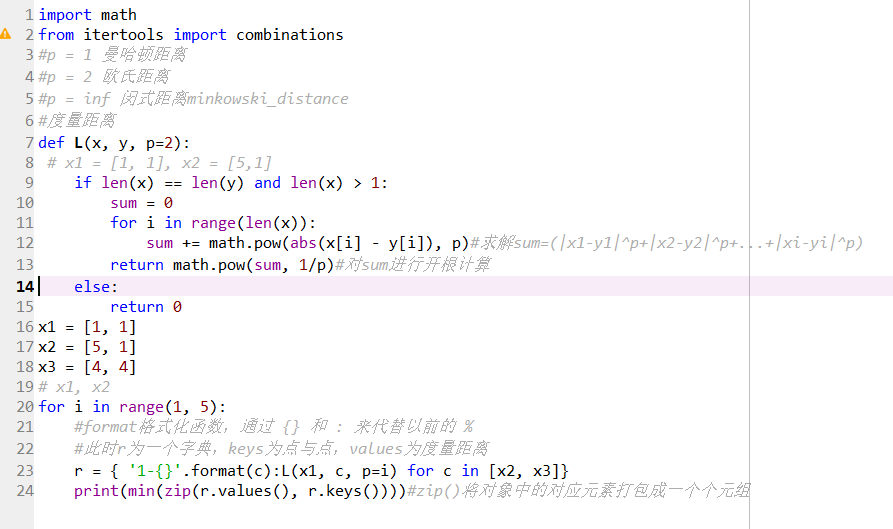
import math
from itertools import combinations
%p = 1 曼哈顿距离
%p = 2 欧氏距离
%p = inf 闵式距离minkowski_distance
2、
%度量距离
def L(x, y, p=2):
%x1 = [1, 1], x2 = [5,1]
if len(x) == len(y) and len(x) > 1:
sum = 0
for i in range(len(x)):
sum += math.pow(abs(x[i] - y[i]), p)#求解sum=(|x1-y1|p+|x2-y2|p+...+|xi-yi|^p)
return math.pow(sum, 1/p)#对sum进行开根计算
else:
return 0
3、
x1 = [1, 1]
x2 = [5, 1]
x3 = [4, 4]
4、
%x1, x2
for i in range(1, 5):
#format格式化函数,通过 {} 和 : 来代替以前的 %
#此时r为一个字典,keys为点与点,values为度量距离
r = { '1-{}'.format(c):L(x1, c, p=i) for c in [x2, x3]}
print(min(zip(r.values(), r.keys())))#zip()将对象中的对应元素打包成一个个元组
5、
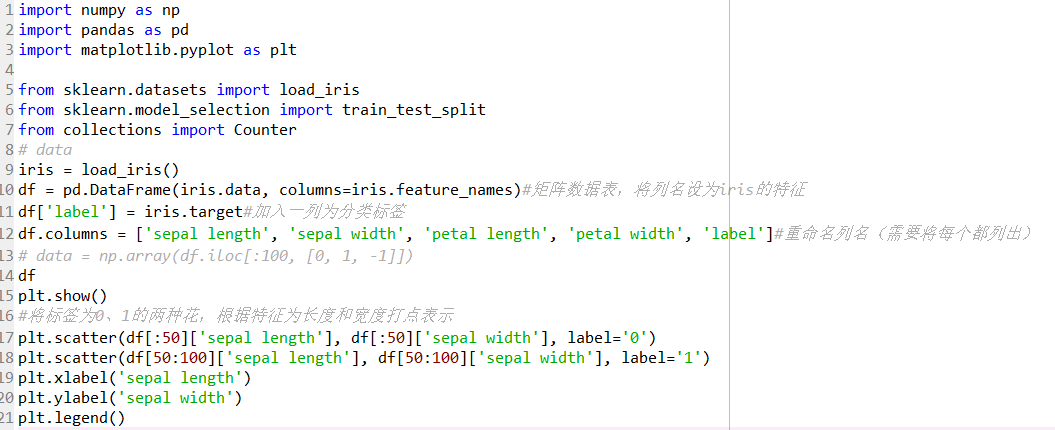
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from collections import Counter
6、
%data
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)#矩阵数据表,将列名设为iris的特征
df['label'] = iris.target#加入一列为分类标签
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']#重命名列名(需要将每个都列出)
% data = np.array(df.iloc[:100, [0, 1, -1]])
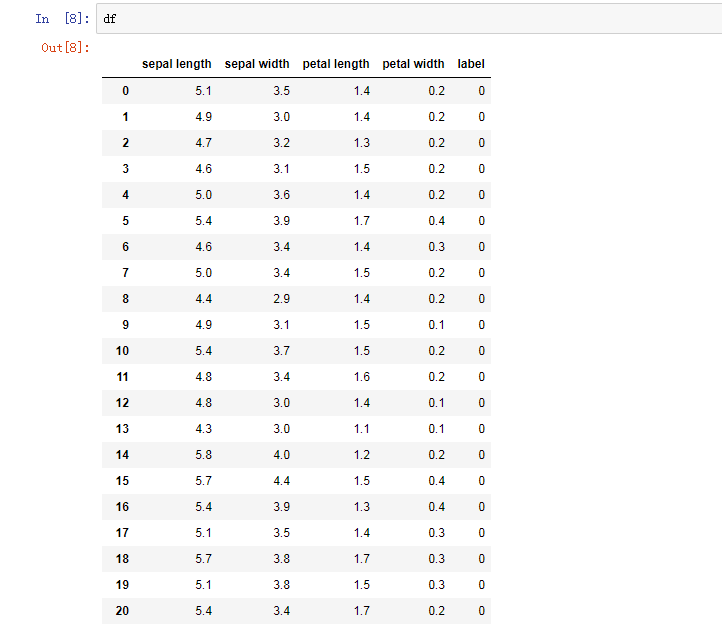
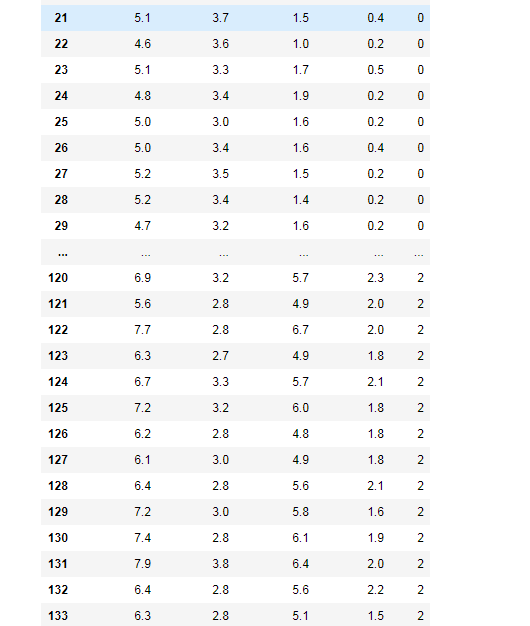
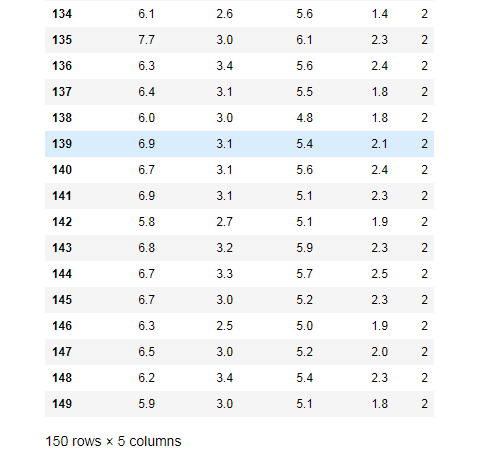
7、
df
8、
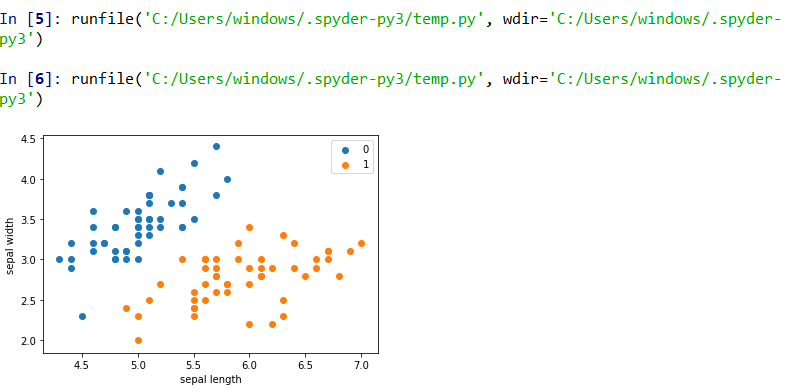
%将标签为0、1的两种花,根据特征为长度和宽度打点表示
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
9、
data = np.array(df.iloc[:100, [0, 1, -1]])#按行索引,取出第0列第1列和最后一列,即取出sepal长度、宽度和标签
X, y = data[:,:-1], data[:,-1]#X为sepal length,sepal width y为标签
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)# train_test_split函数用于将矩阵随机划分为训练子集和测试子集
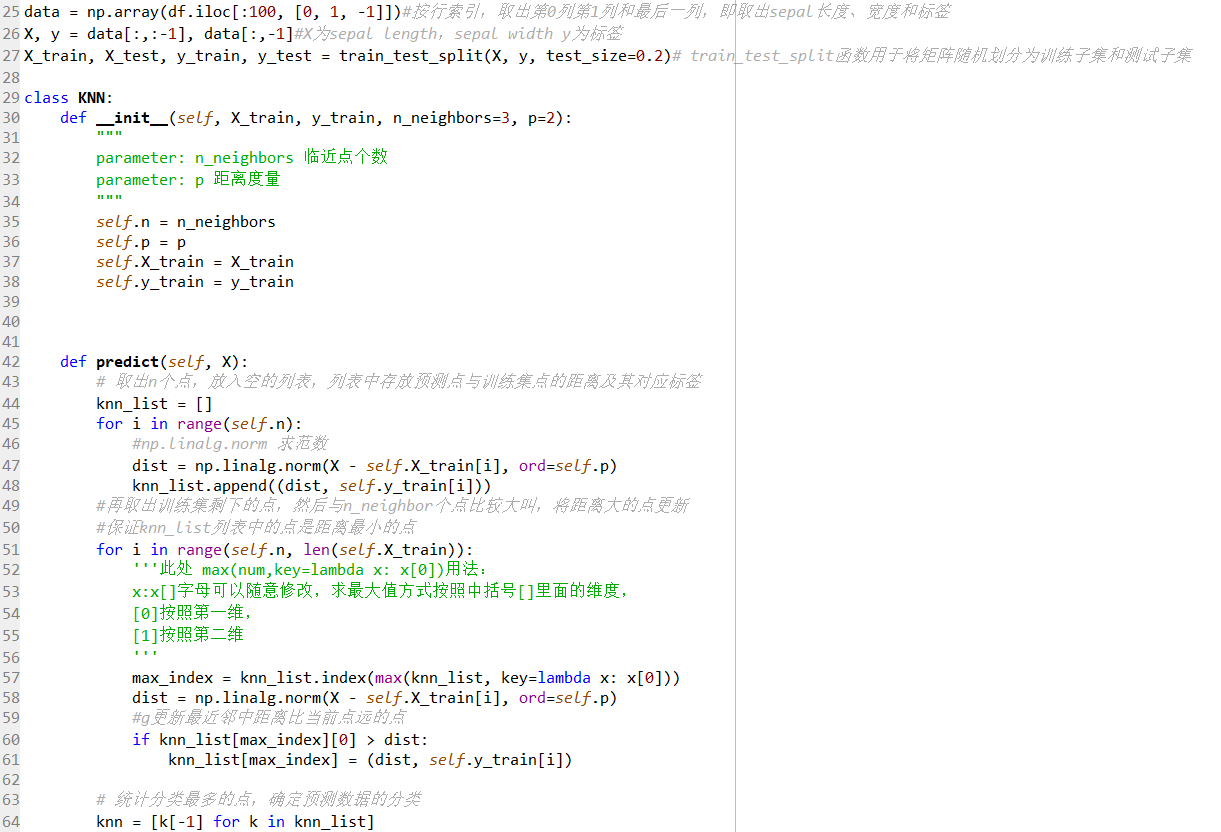
10、
class KNN:
def init(self, X_train, y_train, n_neighbors=3, p=2):
"""
parameter: n_neighbors 临近点个数
parameter: p 距离度量
"""
self.n = n_neighbors
self.p = p
self.X_train = X_train
self.y_train = y_train
def predict(self, X):
# 取出n个点,放入空的列表,列表中存放预测点与训练集点的距离及其对应标签
knn_list = []
for i in range(self.n):
#np.linalg.norm 求范数
dist = np.linalg.norm(X - self.X_train[i], ord=self.p)
knn_list.append((dist, self.y_train[i]))
#再取出训练集剩下的点,然后与n_neighbor个点比较大叫,将距离大的点更新
#保证knn_list列表中的点是距离最小的点
for i in range(self.n, len(self.X_train)):
'''此处 max(num,key=lambda x: x[0])用法:
x:x[]字母可以随意修改,求最大值方式按照中括号[]里面的维度,
[0]按照第一维,
[1]按照第二维
'''
max_index = knn_list.index(max(knn_list, key=lambda x: x[0]))
dist = np.linalg.norm(X - self.X_train[i], ord=self.p)
#g更新最近邻中距离比当前点远的点
if knn_list[max_index][0] > dist:
knn_list[max_index] = (dist, self.y_train[i])
# 统计分类最多的点,确定预测数据的分类
knn = [k[-1] for k in knn_list]
#counter为计数器,按照标签计数
count_pairs = Counter(knn)
#排序
max_count = sorted(count_pairs, key=lambda x:x)[-1]
return max_count
#预测的正确率
def score(self, X_test, y_test):
right_count = 0
n = 10
for X, y in zip(X_test, y_test):
label = self.predict(X)
if label == y:
right_count += 1
return right_count / len(X_test)
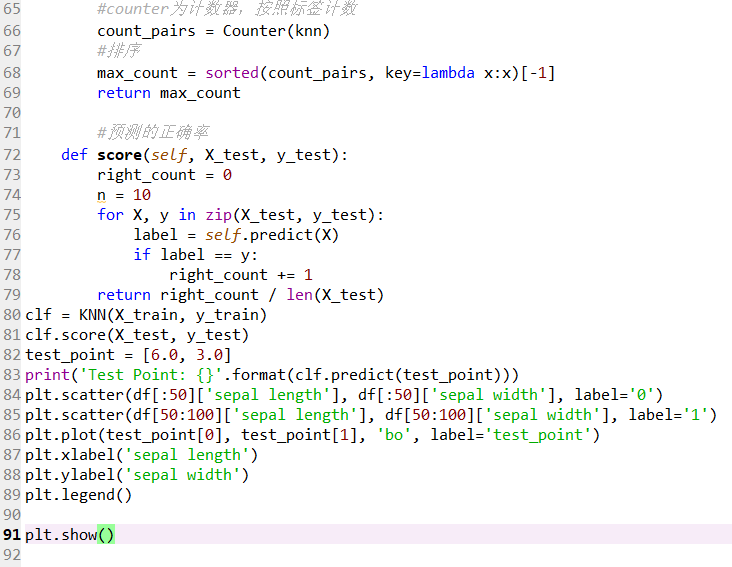
11、
clf = KNN(X_train, y_train)
12、
clf.score(X_test, y_test)
13、
test_point = [6.0, 3.0]#预测点
print('Test Point: {}'.format(clf.predict(test_point)))
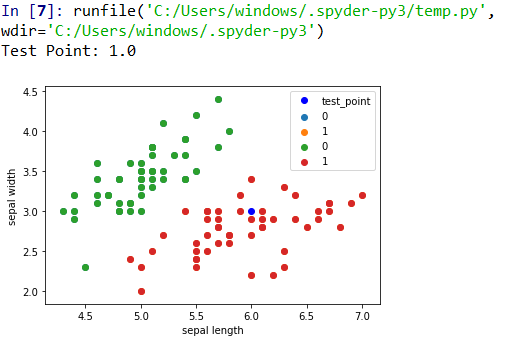
14、
%预测点
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
%打印预测点
plt.plot(test_point[0], test_point[1], 'bo', label='test_point')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
15、
from sklearn.neighbors import KNeighborsClassifier
16、
clf_sk = KNeighborsClassifier()
clf_sk.fit(X_train, y_train)
17、
clf_sk.score(X_test, y_test)
18、
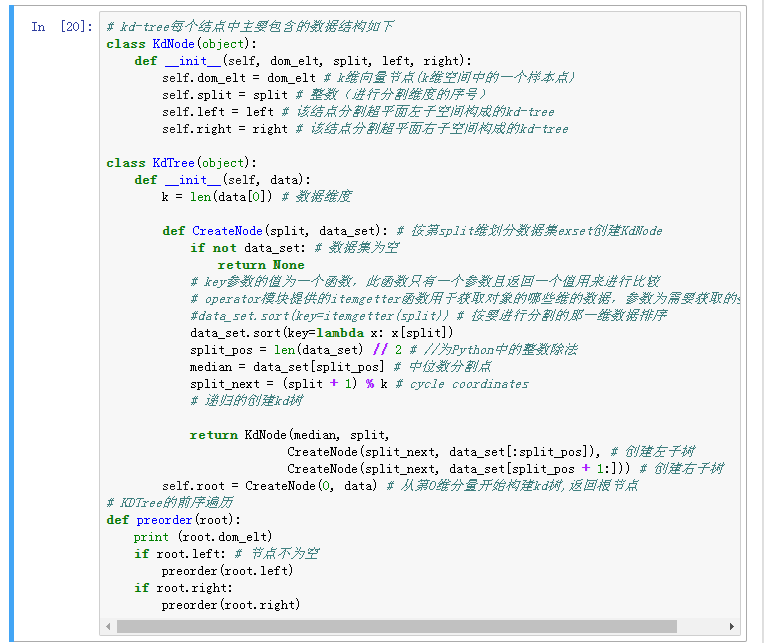
%kd-tree每个结点中主要包含的数据结构如下 class KdNode(object):
def init(self, dom_elt, split, left, right):
self.dom_elt = dom_elt # k维向量节点(k维空间中的一个样本点)
self.split = split # 整数(进行分割维度的序号)
self.left = left # 该结点分割超平面左子空间构成的kd-tree
self.right = right # 该结点分割超平面右子空间构成的kd-tree
class KdTree(object):
def init(self, data):
k = len(data[0]) # 数据维度
def CreateNode(split, data_set): # 按第split维划分数据集exset创建KdNode
if not data_set: # 数据集为空
return None
% key参数的值为一个函数,此函数只有一个参数且返回一个值用来进行比较
% operator模块提供的itemgetter函数用于获取对象的哪些维的数据,参数为需要获取的数据在对象
%data_set.sort(key=itemgetter(split)) # 按要进行分割的那一维数据排序
data_set.sort(key=lambda x: x[split])
split_pos = len(data_set) // 2 # //为Python中的整数除法
median = data_set[split_pos] # 中位数分割点
split_next = (split + 1) % k # cycle coordinates
% 递归的创建kd树
return KdNode(median, split,
CreateNode(split_next, data_set[:split_pos]), # 创建左子树
CreateNode(split_next, data_set[split_pos + 1:])) # 创建右子树
self.root = CreateNode(0, data) # 从第0维分量开始构建kd树,返回根节点
%KDTree的前序遍历 def preorder(root):
print (root.dom_elt)
if root.left: # 节点不为空
preorder(root.left)
if root.right:
preorder(root.right)
19、
%对构建好的kd树进行搜索,寻找与目标点最近的样本点:
from math import sqrt
from collections import namedtuple
%定义一个namedtuple,分别存放最近坐标点、最近距离和访问过的节点数
result = namedtuple("Result_tuple", "nearest_point nearest_dist nodes_visited")
def find_nearest(tree, point):
k = len(point) # 数据维度
def travel(kd_node, target, max_dist):
if kd_node is None:
return result([0] * k, float("inf"), 0) # python中用float("inf")和float("-inf")表示正负
nodes_visited = 1
s = kd_node.split # 进行分割的维度
pivot = kd_node.dom_elt # 进行分割的“轴”
if target[s] <= pivot[s]: # 如果目标点第s维小于分割轴的对应值(目标离左子树更近)
nearer_node = kd_node.left # 下一个访问节点为左子树根节点
further_node = kd_node.right # 同时记录下右子树
else: # 目标离右子树更近
nearer_node = kd_node.right # 下一个访问节点为右子树根节点
further_node = kd_node.left
temp1 = travel(nearer_node, target, max_dist) # 进行遍历找到包含目标点的区域
nearest = temp1.nearest_point # 以此叶结点作为“当前最近点”
dist = temp1.nearest_dist # 更新最近距离
nodes_visited += temp1.nodes_visited
if dist < max_dist:
max_dist = dist # 最近点将在以目标点为球心,max_dist为半径的超球体内
temp_dist = abs(pivot[s] - target[s]) # 第s维上目标点与分割超平面的距离
if max_dist < temp_dist: # 判断超球体是否与超平面相交
return result(nearest, dist, nodes_visited) # 不相交则可以直接返回,不用继续判断
#----------------------------------------------------------------------
# 计算目标点与分割点的欧氏距离
temp_dist = sqrt(sum((p1 - p2) ** 2 for p1, p2 in zip(pivot, target)))
if temp_dist < dist: # 如果“更近”
nearest = pivot # 更新最近点
dist = temp_dist # 更新最近距离
max_dist = dist # 更新超球体半径
# 检查另一个子结点对应的区域是否有更近的点
temp2 = travel(further_node, target, max_dist)
nodes_visited += temp2.nodes_visited
if temp2.nearest_dist < dist: # 如果另一个子结点内存在更近距离
nearest = temp2.nearest_point # 更新最近点
dist = temp2.nearest_dist # 更新最近距离
return result(nearest, dist, nodes_visited)
return travel(tree.root, point, float("inf")) # 从根节点开始递归
20、
data = [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]
kd = KdTree(data)
preorder(kd.root)
21、
from time import clock
from random import random
% 产生一个k维随机向量,每维分量值在0~1之间
def random_point(k):
return [random() for _ in range(k)]
% 产生n个k维随机向量
def random_points(k, n):
return [random_point(k) for _ in range(n)]
22、
ret = find_nearest(kd, [3,4.5])
print (ret)
23、
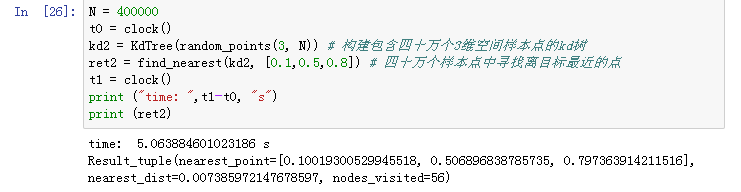
N = 400000
t0 = clock()
kd2 = KdTree(random_points(3, N)) # 构建包含四十万个3维空间样本点的kd树
ret2 = find_nearest(kd2, [0.1,0.5,0.8]) # 四十万个样本点中寻找离目标最近的点
t1 = clock()
print ("time: ",t1-t0, "s")
print (ret2)
二、实验结果截图







四、K近邻的优缺点
优点:
(1)k近邻算法是一种在线技术,新数据可以直接加入数据集而不必进行重新训练,
(2)k近邻算法理论简单,容易实现。
(3)准确性高,对异常值和噪声有较高的容忍度。
(4)k近邻算法天生就支持多分类,区别与感知机、逻辑回归、SVM。
缺点:
(1)基本的 k近邻算法每预测一个“点”的分类都会重新进行一次全局运算,对于样本容量大的数据集计算量比较大。
(2)K近邻算法容易导致维度灾难。在高维空间中计算距离的时候,就会变得非常远;样本不平衡时,预测偏差比较大,k值大小的选择得依靠经验或者交叉验证得到。k的选择可以使用交叉验证,也可以使用网格搜索。k的值越大,模型的偏差越大,对噪声数据越不敏感,当 k的值很大的时候,可能造成模型欠拟合。k的值越小,模型的方差就会越大,当 k的值很小的时候,就会造成模型的过拟合。
五、举例说明K近邻的应用场景
(1)多分类问题场景
在多分类问题中的k邻法,k邻法的输入为实例的特征向量,对应于特征空间的点,输出为实例的类别。
k邻法假设给定一个训练数据集,其中的实例类别已定,分类时,对新的实例,根据其k个最邻的训练实例的类别,通过多数表决等方式进行预测。因此,k邻法不具有显示的学过程(或者说是一种延迟学),k邻法实际上利用训练数据集对特征向量空间进行划分,并作为其分类的“模型”。
(2)回归问题的场景
KNN算法不仅可以用于分类,还可以用于回归。通过找出一个样本的k个最*邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。
更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight),如权值与距离成正比。
六、实验小结
这次实验,加强上机实践。在本次综合实验中,我明白了理论与实际应用相结合的重要性。培养了基本的、良好的程序技能以及合作能力。这次实验同样提高了我的综合运用所学知识的能力。