某个子集中。点的权值是这样算的。在该子集中这个点的度除以该点在图中的度。
乍看上去似乎无从下手。
能够显然知道的是。每一个点在图中的权值是非常easy算出来的,那我们尝试从图中进行删点。使得当前图的最小权值点的权值变大,显然能够知道要删除最小权值点。为什么呢?由于若删除次小权值点,若次小权值点跟最小权值点有连边,那最小权值点还是新图的最小权值点。若没有连边,那新图的最小权值点也依然未变。
所以仅仅有删除最小权值点才有可能改变新图的最小权值点,也仅仅有这样能让新图的最小权值发生改变。
那么到这里就十分明显了,仅仅要每次删除当前图的最小权值点。那么必定能够枚举出一个新图。这个新图的点构成的点集正是我们要的答案。
于是这个题就能够做了,我是直接做了两次删除,第一次得出最大最小权值是多少,第二次枚举到一个新图的最小权值等于最大最小权值。那么非常显然这个新图的子集就是答案。
维护一个小堆就好了,时间复杂度是2(n+m)log(n+m)
#include<map>
#include<string>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<vector>
#include<iostream>
#include<algorithm>
#include<bitset>
#include<climits>
#include<list>
#include<iomanip>
#include<stack>
#include<set>
using namespace std;
struct node
{
int no;
double val;
node(){}
node(int no,double val)
{
this->no=no;
this->val=val;
}
bool operator <(node one)const
{
return val>one.val;
}
};
priority_queue<node>q[2];
bool fb[100010],dl[100010];
vector<int>edge[100010];
int d[100010][2],dd[100010];
int main()
{
int n,m,k;
cin>>n>>m>>k;
int sum=k;
while(k--)
{
int t;
cin>>t;
fb[t]=1;
}
while(m--)
{
int a,b;
cin>>a>>b;
d[a][0]++;
d[b][0]++;
if(!fb[a])
d[b][1]++;
if(!fb[b])
d[a][1]++;
edge[a].push_back(b);
edge[b].push_back(a);
}
double mn=1e99;
for(int i=1;i<=n;i++)
if(!fb[i])
{
q[0].push(node(i,double(d[i][1])/d[i][0]));
mn=min(mn,double(d[i][1])/d[i][0]);
}
q[1]=q[0];
int flag=0;
for(int i=0;i<2;i++)
{
memset(dl,0,sizeof(dl));
memset(dd,0,sizeof(dd));
if(i==1&&flag==0)
break;
while(q[i].size())
{
node t=q[i].top();
q[i].pop();
if(dl[t.no])
continue;
if(i==1)
{
if(t.no==flag)
break;
sum++;
}
dl[t.no]=1;
if(i==0&&t.val>mn)
{
mn=t.val;
flag=t.no;
}
for(int j=0;j<edge[t.no].size();j++)
{
int v=edge[t.no][j];
if(dl[v]||fb[v])
continue;
dd[v]++;
q[i].push(node(v,double(d[v][1]-dd[v])/d[v][0]));
}
}
}
cout<<n-sum<<endl;
for(int i=1;i<=n;i++)
if(!fb[i]&&!dl[i])
cout<<i<<" ";
}Nudist Beach is planning a military operation to attack the Life Fibers. In this operation, they will attack and capture several cities which are currently under the control of the Life Fibers.
There are n cities, labeled from 1 to n, and m bidirectional roads between them. Currently, there are Life Fibers in every city. In addition, there are k cities that are fortresses of the Life Fibers that cannot be captured under any circumstances. So, the Nudist Beach can capture an arbitrary non-empty subset of cities with no fortresses.
After the operation, Nudist Beach will have to defend the captured cities from counterattack. If they capture a city and it is connected to many Life Fiber controlled cities, it will be easily defeated. So, Nudist Beach would like to capture a set of cities such that for each captured city the ratio of Nudist Beach controlled neighbors among all neighbors of that city is as high as possible.
More formally, they would like to capture a non-empty set of cities S with no fortresses of Life Fibers. The strength of a city 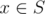 is
defined as (number of neighbors of x in S)
/ (total number of neighbors of x). Here, two cities are called neighbors if they are connnected with a road. The goal is to maximize
the strength of the weakest city in S.
is
defined as (number of neighbors of x in S)
/ (total number of neighbors of x). Here, two cities are called neighbors if they are connnected with a road. The goal is to maximize
the strength of the weakest city in S.
Given a description of the graph, and the cities with fortresses, find a non-empty subset that maximizes the strength of the weakest city.
The first line of input contains three integers n, m, k (2 ≤ n ≤ 100 000, 1 ≤ m ≤ 100 000, 1 ≤ k ≤ n - 1).
The second line of input contains k integers, representing the cities with fortresses. These cities will all be distinct.
The next m lines contain the roads. The i-th of these lines will have 2 integers ai, bi (1 ≤ ai, bi ≤ n, ai ≠ bi). Every city will have at least one road adjacent to it.
There is no more than one road between each pair of the cities.
The first line should contain an integer r, denoting the size of an optimum set (1 ≤ r ≤ n - k).
The second line should contain r integers, denoting the cities in the set. Cities may follow in an arbitrary order. This line should not contain any of the cities with fortresses.
If there are multiple possible answers, print any of them.
9 8 4 3 9 6 8 1 2 1 3 1 4 1 5 2 6 2 7 2 8 2 9
3 1 4 5
10 8 2 2 9 1 3 2 9 4 5 5 6 6 7 7 8 8 10 10 4
8 1 5 4 8 10 6 3 7
The first example case achieves a strength of 1/2. No other subset is strictly better.
The second example case achieves a strength of 1. Note that the subset doesn't necessarily have to be connected.