AtCoder Beginner Contest 058 ABCD题

A - ι⊥l

---

Time limit : 2sec / Memory limit : 256MB

Score : 100 points

Problem Statement

Three poles stand evenly spaced along a line. Their heights are a, b and c meters, from left to right. We will call the arrangement of the poles beautiful if the tops of the poles lie on the same line, that is, b−a=c−b.

Determine whether the arrangement of the poles is beautiful.

Constraints

• 1≤a,b,c≤100
• a, b and c are integers.

---

Input

Input is given from Standard Input in the following format:

a b c

Output

Print YES if the arrangement of the poles is beautiful; print NO otherwise.

---

Sample Input 1

Copy

2 4 6

Sample Output 1

Copy

YES

Since 4−2=6−4, this arrangement of poles is beautiful.

---

Sample Input 2

Copy

2 5 6

Sample Output 2

Copy

NO

Since 5−2≠6−5, this arrangement of poles is not beautiful.

---

Sample Input 3

Copy

3 2 1

Sample Output 3

Copy

YES

Since 1−2=2−3, this arrangement of poles is beautiful.

题意：额。。

解法：额

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
 
ll an[100010],am[100010];
int main()
{
    int a,b,c;
    cin>>a>>b>>c;
    if(b-a==c-b)
    {
        cout<<"YES"<<endl;
    }
    else
    {
        cout<<"NO"<<endl;
    }
    return 0;
}

B - ∵∴∵

---

Time limit : 2sec / Memory limit : 256MB

Score : 200 points

Problem Statement

Snuke signed up for a new website which holds programming competitions. He worried that he might forget his password, and he took notes of it. Since directly recording his password would cause him trouble if stolen, he took two notes: one contains the characters at the odd-numbered positions, and the other contains the characters at the even-numbered positions.

You are given two strings O and E. O contains the characters at the odd-numbered positions retaining their relative order, and E contains the characters at the even-numbered positions retaining their relative order. Restore the original password.

Constraints

• O and E consists of lowercase English letters (a - z).
• 1≤|O|,|E|≤50
• |O|−|E| is either 0 or 1.

---

Input

Input is given from Standard Input in the following format:

O
E

Output

Print the original password.

---

Sample Input 1

Copy

xyz
abc

Sample Output 1

Copy

xaybzc

The original password is xaybzc. Extracting the characters at the odd-numbered positions results in xyz, and extracting the characters at the even-numbered positions results in abc.

---

Sample Input 2

Copy

atcoderbeginnercontest
atcoderregularcontest

Sample Output 2

Copy

aattccooddeerrbreeggiunlnaerrccoonntteesstt
题意：额
解法：额

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
string s1,s2,s3;
int main()
{
    int num1=0;
    int num2=0;
    cin>>s1;
    cin>>s2;
    for(int i=0;i<s1.size()+s2.size();i++)
    {
        if(i%2)
        {
            cout<<s2[num1++];
        }
        else
        {
            cout<<s1[num2++];
        }
    }
    cout<<endl;
    return 0;
}

C - 怪文書 / Dubious Document

---

Time limit : 2sec / Memory limit : 256MB

Score : 300 points

Problem Statement

Snuke loves "paper cutting": he cuts out characters from a newspaper headline and rearranges them to form another string.

He will receive a headline which contains one of the strings S1,…,Sn tomorrow. He is excited and already thinking of what string he will create. Since he does not know the string on the headline yet, he is interested in strings that can be created regardless of which string the headline contains.

Find the longest string that can be created regardless of which string among S1,…,Sn the headline contains. If there are multiple such strings, find the lexicographically smallest one among them.

Constraints

• 1≤n≤50
• 1≤|S_i|≤50 for every i=1,…,n.
• Si consists of lowercase English letters (a - z) for every i=1,…,n.

---

Input

Input is given from Standard Input in the following format:

n
S1
…
Sn

Output

Print the lexicographically smallest string among the longest strings that satisfy the condition. If the answer is an empty string, print an empty line.

---

Sample Input 1

Copy

3
cbaa
daacc
acacac

Sample Output 1

Copy

aac

The strings that can be created from each of cbaa, daacc and acacac, are aa, aac, aca, caa and so forth. Among them, aac, aca andcaa are the longest, and the lexicographically smallest of these three is aac.

---

Sample Input 2

Copy

3
a
aa
b

Sample Output 2

Copy

The answer is an empty string.

题意：选择字符串公共的字母，哪个字母出现次数最少就加进去，比如a在第一个字符串只出现了次，于是有aa

解法：模拟

#include <bits/stdc++.h>

using namespace std;
string s[100];
int n;
map<char,int>q;
string s1;
int main()
{
    cin>>n;
    for(int i=0; i<n; i++)
    {
        cin>>s[i];
    }
    for(char i='a'; i<='z'; i++)
    {
        int flag=0;
        for(int j=0; j<n; j++)
        {
            if(s[j].find(i)==-1)
            {
                flag=1;
            }
        }
        if(flag==0)
        {
            int minn=100;
           // cout<<i<<endl;
            for(int j=0; j<n; j++)
            {
                int cnt=0;
                for(int z=0;z<s[j].size();z++)
                {
                    if(s[j][z]==i)
                    {
                        cnt++;
                    }
                }
                minn=min(minn,cnt);
            }
            for(int j=0;j<minn;j++)
            {
                s1+=i;
            }
        }
    }
    cout<<s1<<endl;
    return 0;
}

D - 井井井 / ###

---

Time limit : 2sec / Memory limit : 256MB

Score : 500 points

Problem Statement

On a two-dimensional plane, there are m lines drawn parallel to the x axis, and n lines drawn parallel to the y axis. Among the lines parallel to the x axis, the i-th from the bottom is represented by y=yi. Similarly, among the lines parallel to the y axis, the i-th from the left is represented by x=xi.

For every rectangle that is formed by these lines, find its area, and print the total area modulo 109+7.

That is, for every quadruple (i,j,k,l) satisfying 1≤i<j≤n and 1≤k<l≤m, find the area of the rectangle formed by the lines x=xi, x=xj, y=yk and y=yl, and print the sum of these areas modulo 109+7.

Constraints

• 2≤n,m≤10⁵
• −10⁹≤x₁<…<x_n≤10⁹
• −109≤y₁<…<y_m≤10⁹
• x_i and y_i are integers.

---

Input

Input is given from Standard Input in the following format:

n m
x1 x2 … xn
y1 y2 … ym

Output

Print the total area of the rectangles, modulo 109+7.

---

Sample Input 1

Copy

3 3
1 3 4
1 3 6

Sample Output 1

Copy

60

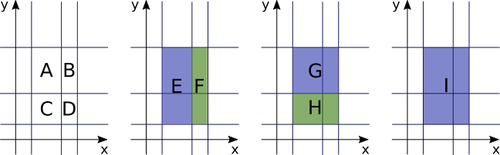
The following figure illustrates this input:

The total area of the nine rectangles A, B, ..., I shown in the following figure, is 60.

---

Sample Input 2

Copy

6 5
-790013317 -192321079 95834122 418379342 586260100 802780784
-253230108 193944314 363756450 712662868 735867677

Sample Output 2

Copy

835067060
题意：把这里面所有的正方形面积都加一次
解法：  ∑∑(xi-xj)(yi-yj)1<=i<=n 1<=j<=m
把上面分开有：

于是...就出来了

#include<bits/stdc++.h>
//std::ios::sync_with_stdio(false);
using namespace std;
typedef long long ll;
ll n,m;
ll sx;
ll sy;
ll mod=1e9+7;
ll x[200000],y[200000];
int main()
{
    cin>>n>>m;
    for(ll i=1;i<=n;i++)
    {
        cin>>x[i];
    }
    for(ll i=1;i<=m;i++)
    {
        cin>>y[i];
    }
    for(ll i=1;i<=n;i++)
    {
        sx+=((i-1)*x[i]-(n-i)*x[i])%mod;
        sx%=mod;
    }
    for(ll i=1;i<=m;i++)
    {
        sy+=((i-1)*y[i]-(m-i)*y[i])%mod;
        sy%=mod;
    }
    cout<<sx%mod*sy%mod<<endl;
    return 0;
}